Hess's law states that if a reaction alone represents two or more other reactions, the heat this reaction releases or absorbs is equal to the sum of the heat released or absorbed by the other reactions.
Some chemical reactions appear to be very simple. However, they are often the result of a complex process requiring many intermediate reactions to go from reactants to products. This sequence of simple reactions forms a reaction mechanism that is summarised by the balanced equation of a complex reaction. The overall heat of the complex reaction can be determined mathematically using Hess's law, also known as the law of enthalpies addition.
A reaction mechanism is a chronological sequence of intermediate reactions leading from the reactants to the products of a complex reaction.
A chemical reaction is generally represented by a balanced equation containing reactants that are transformed into products. However, this simple representation gives no information about how the chemical reaction takes place. In majority chemical reactions, the reactants are not directly transformed into products. Instead, they become a series of intermediate substances that ultimately lead to the final products. A complex reaction can be divided into a series of intermediate reactions. This is known as a reaction mechanism.
A reaction mechanism can be represented by the sum of a series of intermediate reactions. This gives the equation for the complex reaction. This equation can be used to summarise the reaction mechanism of the complex reaction without indicating the intermediate steps it contains.
The formation of nitrogen dioxide from nitrogen oxide and oxygen gas is a complex reaction involving two intermediate stages.
||\begin{align*}2\ NO_{(g)} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{N_2O_{2(g)}}}\\
\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{N_2O_{2(g)}}} + O_{2(g)} \quad &\rightarrow \quad 2\ NO_{2(g)}\\
\overline{\phantom{^4}2\ NO_{(g)} + O_{2(g)} \quad} &\overline{\;\rightarrow \quad 2\ NO_{2(g)}\phantom{^4}}\end{align*}||
A reaction mechanism can also be represented with an energy diagram. In such a diagram, each stage is an intermediate reaction in which the product of the first reaction becomes the reactant of the second, until the final products are produced. Each reaction has its own activation energy and enthalpy variation.
The reaction mechanism of a hypothetical complex reaction from reactant A to product E takes place in four distinct stages.
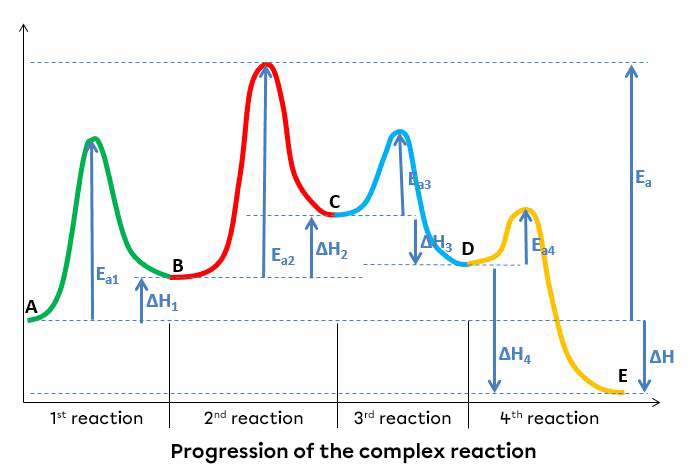
The step with the highest activation energy is the one that determines the reaction rate. The higher is the activation energy, the slower is the step rate. In the graph above, the second reaction is the slowest step, since it has the highest activation energy.
Hess's law states that when a reaction can be divided into several elementary reactions, the overall enthalpy variation of the complex reaction is equal to the sum of the enthalpy variations of each intermediate reactions.
In 1840, the Swiss chemist Germain Henri Hess (1802-1850) developed a method for predicting the variation in enthalpy generated by chemical reactions. This method, known as Hess's law, is very useful in situations where it is impossible to perform certain reactions in laboratory. This is especially true of reactions that are too fast, too slow or too violent.
When Hess was working on the law, he noticed that the enthalpy variation of a reaction is the same whether the reaction takes place in one or more stages. This means that the variation only depends on reactants and products, independently of the reaction mechanism and the number of intermediate steps required to complete the reaction. This law can be expressed mathematically by the following equation:
|\triangle H=\triangle H_{1}+\triangle H_{2}+\triangle H_{3}+...|
where
|\triangle H| represents the overall enthalpy variation in kJ/mol
|\triangle H_{1},\triangle H_{2},\triangle H_{3}| represent the enthalpy variation of each of the intermediate reactions in the overall reaction in kJ/mol
The reaction enthalpy therefore remains the same whether the reaction proceeds directly from the reactants to the products or whether it takes place in several stages. For example, the formation of carbon dioxide can take place through two different mechanisms.
Two mechanisms are responsible for the formation of carbon dioxide:
1. Carbon dioxide can be produced directly by the reaction of carbon in contact with oxygen. This reaction can be summarised as follows:
||C_{(s)} + O_{2(g)} \rightarrow CO_{2(g)} \hspace {25 mm}ΔH = -393.5 \:\text{kJ/mol}||
2. This reaction can also take place in two steps. ||\begin{align*} C_{(s)} + 1/2\ O_{2(g)} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{CO_{(g)}}} & &\Delta H_1= -110.5\:\text{kJ/mol}\\ \enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{CO_{(g)}}} + 1/2\ O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} & &\Delta H_2= -283.0\:\text{kJ/mol}\\ \hline {\phantom{CO_2^4} C_{(s)} + O_{2(g)} \quad} &{\phantom{^4}\;\rightarrow \quad CO_{2(g)}} & &{\Delta H= -393.5\:\text{kJ/mol}\phantom{^4}} \end{align*}||
We can see that, no matter which reaction mechanism is used, the result is the same, in other words the production of one mole of carbon dioxide from one mole of solid carbon and one mole of gaseous oxygen. Also, the enthalpy variation is the same in both mechanisms.
To determine the heat of a reaction using Hess's law, certain rules must be followed.
- Identical terms on the same side of the equation are summed.
- Identical terms on opposite sides of the equation are subtracted.
- If you reverse an equation, you must also reverse the sign of the |\triangle H|.
- If we change the coefficients of a chemical equation by multiplying or dividing them by a common factor, we must also multiply or divide the value of the |\triangle H| by the same common factor.
To help calculate the heat of a reaction using Hess's law, you can follow the steps listed below. Obviously, some of these steps may not always be necessary, depending on the case.
Steps to follow to calculate the heat of a reaction using Hess's law
- Write the balanced overall equation.
- Choose the relevant intermediate equations.
- Rearrange the equations by reversing or multiplying them.
- Sum the equations and their associated heats.
- Convert the value obtained according to the specifications of the problem.
What is the molar heat of methane synthesis from solid carbon and hydrogen gas?
1. Global chemical equation
||C_{(s)} + 2\ H_{2(g)} \rightarrow CH_{4(g)}||
2. Intermediate chemical equations
||\begin{align*} &1)&\ C_{(s)} + O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} & &\Delta H_1= -394.1\:\text{kJ/mol}\\ &2)&\ H_{2(g)} + 1/2\ O_{2(g)} \quad &\rightarrow \quad H_2O_{(g)} & &\Delta H_2= -242.2\:\text{kJ/mol}\\ &3)&\ CH_{4(g)} + 2\ O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} + 2\ H_2O_{(g)} & &\Delta H_3= -803.6\:\text{kJ/mol} \end{align*}||
3. Handling intermediate chemical equations
We have to reverse the third reaction and multiply the second reaction by 2. The result is :
||\begin{align*} &1)&\ C_{(s)} + O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} & &\Delta H_1= -394.1\:\text{kJ/mol}\\ &2)&\ 2\ H_{2(g)} + O_{2(g)} \quad &\rightarrow \quad 2\ H_2O_{(g)} & &\Delta H_2= -484.4\:\text{kJ/mol}\\ &3)&\ CO_{2(g)} + 2\ H_2O_{(g)} \quad &\rightarrow \quad CH_{4(g)} + 2\ O_{2(g)} & &\Delta H_3= +803.6\:\text{kJ/mol} \end{align*}||
4. Equations addition
||\begin{align*} &1)&\ C_{(s)} + \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{O_{2(g)}}} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{CO_{2(g)}}} & &\Delta H_1= -394.1\:\text{kJ/mol}\\ &2)&\ 2\ H_{2(g)} + \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{O_{2(g)}}} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{2 \: H_2O_{(g)}}} & &\Delta H_2= -484.4\:\text{kJ/mol}\\ &3)&\ \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{CO_{2(g)}}} + \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{2\ H_2O_{(g)}}} \quad &\rightarrow \quad CH_{4(g)} + \enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{2\ O_{2(g)}}} & &\Delta H_3= +803.6\:\text{kJ/mol} \\ \hline &&\ C_{(s)} + 2\ {H_{2(g)}} \quad &\rightarrow \quad {CH_{4(g)}} & &\Delta H_{ }= -74.9\:\text{kJ/mol} \end{align*}||
5. Answer: The molar heat of reaction is |-74.9\:\text{kJ/mol}|.
What is the reaction heat of propane combustion?
1. Global chemical equation
||C_{3}H_{8(g)} + 5\ O_{2(g)} \rightarrow 3\ CO_{2(g)} + 4\ H_{2}O_{(g)}||
2. Intermediate chemical equations
||\begin{align*} &1)&\ H_{2(g)} + 1/2\ O_{2(g)} \quad &\rightarrow \quad H_2O_{(g)} & &\Delta H_1= -242.2\:\text{kJ/mol}\\ &2)&\ 3\ C_{(s)} + 4\ H_{2(g)} \quad &\rightarrow \quad C_3H_{8(g)} & &\Delta H_2= -103.8\:\text{kJ/mol}\\ &3)&\ C_{(s)} + O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} & &\Delta H_3= -394.1\:\text{kJ/mol} \end{align*}||
3. Handling intermediate chemical equations
We have to multiply the first equation by 4, invert the second equation and finally multiply the third reaction by 3.
||\begin{align*} &1)&\ 4\ H_{2(g)} + 2\ O_{2(g)} \quad &\rightarrow \quad 4\ H_2O_{(g)} & &\Delta H_1= -968.8\:\text{kJ/mol}\\ &2)&\ C_3H_{8(g)} \quad &\rightarrow \quad 3\ C_{(s)} + 4\ H_{2(g)} & &\Delta H_2= +103.8\:\text{kJ/mol}\\ &3)&\ 3\ C_{(s)} + 3\ O_{2(g)} \quad &\rightarrow \quad 3\ CO_{2(g)} & &\Delta H_3= -1\:182.3\:\text{kJ/mol} \end{align*}||
4. Equations addition
||\begin{align*} &1)&\ \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{4\ H_{2(g)}}}+ 2\ O_{2(g)} \quad &\rightarrow \quad 4\ H_2O_{(g)} & &\Delta H_1= -968.8\:\text{kJ/mol}\\ &2)&\ C_3H_{8(g)} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{3\ C_{(s)}}} + \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{4\ H_{2(g)}}} & &\Delta H_2= +103.8\:\text{kJ/mol}\\ &3)&\ \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{3\ C_{(s)}}} + 3\ O_{2(g)} \quad &\rightarrow \quad 3\ CO_{2(g)} & &\Delta H_3= -1\:182.3\:\text{kJ/mol} \\ \hline &&C_{3}H_{8(g)} + 5\ O_{2(g)} \quad &\rightarrow \quad 3\ CO_{2(g)} + 4\ H_{2}O_{(g)} & &\Delta H_{ }= -2\:047.3\:\text{kJ/mol} \end{align*} ||
5. Answer: The molar heat of reaction is |-2\:047.3\:\text{kJ/mol}|.