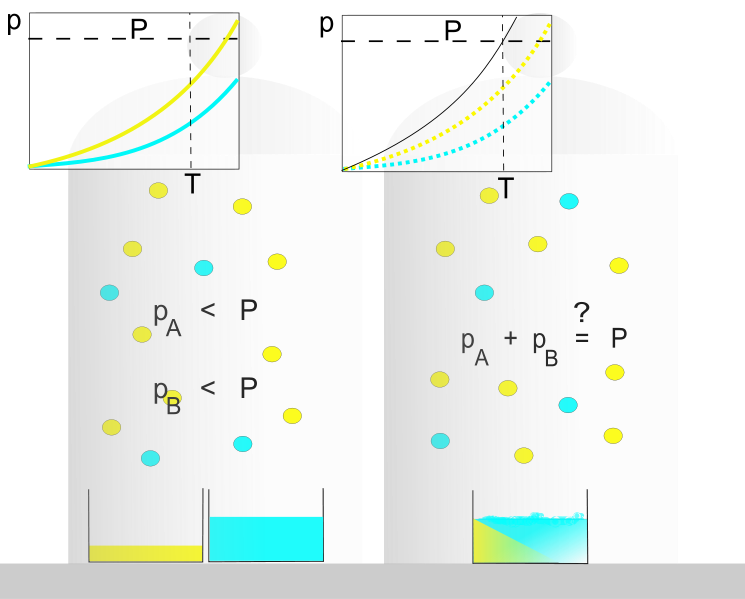
The law of partial pressures states that, at a given temperature, the total pressure of a gaseous mixture is equal to the sum of the partial pressures exerted by each of the gases making up the mixture.
The English scientist John Dalton (1766-1844) observed that, in a mixture made up of several gases, the sum total of each of the pressures exerted by the different gases corresponds to the total pressure of the mixture. This means that each gas in a mixture acts as if it alone occupied all the available space in the container. Each gas therefore exerts the same pressure as if it were alone, its behaviour not being influenced by the presence of the other gases.
Graphical representation of the law of partial pressures: On the left are the pressures exerted by gases A and B if they were alone in the container. On the right is the pressure exerted by the mixture of gases A and B in the same container. Note that the pressure of the mixture is equal to the sum of the pressures exerted by each gas individually.
The individual pressure exerted by each of the gases in a container is called the partial pressure.
This pressure represents only a component of the total pressure exerted by all the gases contained in the container. Mathematically, the law of partial pressures, also known as Dalton's law, can be expressed as follows:
Dalton's law:
|P_{total} = P_{1} + P_{2} + P_{3} + P_{4} ...|
where
|P_{total}| represents the total pressure (in kPa or mm Hg)
|P_{1}| represents the partial pressure of gas 1 (in kPa or mm Hg)
|P_{2}| represents the partial pressure of gas 2 (in kPa or mm Hg)
|P_{3}| represents the partial pressure of gas 3 (in kPa or mm Hg)
|P_{4}| represents the partial pressure of gas 4 (in kPa or mm Hg)
This law applies to any mixture of gases, regardless of the number of gases in the mixture. It also applies when a gas is collected by water displacement. In this technique, a certain amount of water vapour is mixed with the resulting gas. To calculate the actual pressure exerted by the gas, the pressure of the water vapour must be subtracted from the total pressure of the mixture collected.
The partial pressure exerted by a gas can also be determined by multiplying the total pressure of the mixture by the molar proportion that the gas represents in the mixture. The formula to be used is as follows:
|\displaystyle P_{1} = P_{total}\times \frac{n_{1}}{n_{total}}|
where
|P_{1}| represents the partial pressure of gas 1 (in kPa or mm Hg)
|P_{total}| represents the total pressure (in kPa or mm Hg)
|n_{1}| represents the quantity of gas 1 (in mol)
|n_{total}| represents the total quantity of the gas mixture (in mol)
A flask contains a mixture of 36 g of carbon dioxide (|CO_{2}|) and 6.0 moles of nitrogen (|N_{2}|). The total pressure of the system is 253 kPa. What is the partial pressure of each of these gases?
- Identification of the problem data:
|n_{1} = \displaystyle \frac {m}{M} = \frac {36 g}{44g/mol} = 0.82 \text { mol of }CO_{2}|
|n_{2} = 6.0 \text { mol of }N_{2}|
|n_{total} = (0.82 + 6.0) \text { mol} = 6.82 \text {mol }|
|P_{total} = 253\ kPa | - Calculation of the partial pressure of |CO_{2}|:
|P_{1} = \displaystyle P_{total}\times \frac{n_{1}}{n_{total}}|
|P_{1} = \displaystyle 253 kPa\times \frac{0.82mol}{6.82mol}|
|P_{1} = 30.4\ kPa| - Calculation of the partial pressure of |N_{2}|:
|P_{2} = \displaystyle P_{total}\times \frac{n_{2}}{n_{total}}|
|P_{2} = \displaystyle 253\ kPa\times \frac{6.0mol}{6.82mol}|
|P_{2} = 222.6\ kPa| - Checking the total pressure:
|30.4\ kPa + 222.6\ kPa = 253\ kPa|