It is possible to simplify an algebraic expression by multiplying its terms. Multiplying two polynomials together is the same as multiplying each of the first polynomial’s terms by each of the second.
There are three steps to perform when multiplying algebraic expressions:
-
Reduce the expression, if necessary, by adding or subtracting like terms (prior to multiplying).
-
Perform the multiplication.
-
Reduce the resulting expression, if necessary, by adding or subtracting like terms.
When multiplying algebraic expressions, two important rules must be followed, which are based on the commutative property of multiplication.
A. Multiply the numbers together and the variables together. ||3x \times 4y = 3 \times 4 \times x\times y = 12xy|| B. When multiplying two identical variables together, add their exponents. ||x^2y^3\times x^3y^7 = x^2 \times x^3 \times y^3\times y^7 = x^{(2+3)}\times y^{(3+7)} = x^5y^{10}||
All terms, whether they are like terms or not, can be multiplied together. However, only like terms can be added or subtracted together.
Rarely do equations consist only of multiplications, but when this does occur, make sure to respect the order of operations when reducing the algebraic expression.
To multiply algebraic expressions, it is essential to master the properties and laws of exponents. The distributive property must be applied as well. When multiplying algebraic expressions, several situations can occur:
When multiplying a monomial by a monomial, first multiply the coefficients together and then add together the exponents of identical variables.
When multiplying a constant term by a monomial, multiply the coefficient of the monomial by the constant term.
Let the constant term be |-3| and the monomial be |4xy^2|.
Perform the multiplication |-3\times 4xy^2|.
Multiply the constant term by the coefficient of the monomial:
||-3 \times 4 = -12||
Write the final answer by adding the variables that were temporarily set aside:
||-3\times 4xy^2 = -12xy^2||
When multiplying two monomials together, multiply the coefficients of the two monomials and add together the exponents of identical variables.
Consider the following two monomials: |-3x^3y^4| and |4xy^2|.
Carry out the multiplication of |-3x^{3}y^4\times 4xy^2|.
Multiply the coefficients together:
||-3\times 4 = -12||
Add the exponents of identical variables:
||x^{(3+1)}\quad \text{and}\quad y^{(4+2)}||
Write the final answer:
||-3x^{3}y^4\times 4xy^{2} = -12x^{4}y^{6}||
Here are the steps in detail:
||\begin{align} -3x^{3}y^4 \times 4xy^2 &= (-3\times {4}) {(x^{3}\times {x})}{(y^{4}\times {y^{2}})}\\
&=(-12){(x^{3+1})}{(y^{4+2})}\\
&=(-12){(x^{4})}{(y^{6})}\\
&=-12x^{4}y^{6}\end{align}||
When multiplying a monomial by a polynomial, apply the distributive property of multiplication over addition and multiply the monomial by each term of the polynomial.
In each multiplication, make sure to multiply the coefficients.
In each multiplication, make sure to add the exponents of identical variables.
Don’t forget to put the polynomial in brackets.
Let the constant term be |1{.}5| and the polynomial be |2xy-x+5y|.
Perform the multiplication by placing the polynomial in brackets:
||1{.}5 (2xy-x+5y)||
Apply the distributive property of multiplication over addition and multiply each term of the polynomial by the constant term:
||\begin{align}\color{red}{1{.}5}(\color{blue} {2xy}\color{green} {-x}\color{fuchsia} {+5y}) &= (\color{red} {1{.}5}\times \color{blue} {2xy}) + (\color{red} {1{.}5}\times \color{green} {-x})+(\color{red} {1{.}5}\times \color{fuchsia} {+5y})\\ &= 3xy + -1{.}5x + 7{.}5y \\ &= 3xy - 1{.}5x + 7{.}5y \end{align}||
Let the monomial be |-3x^3y^4| and the binomial be |4xy^2+2xy.| Place the binomial in brackets:
||-3x^{3}y^{4}(4xy^{2} + 2xy)||
Apply the distributive property and multiply each term of the binomial by the monomial.
Here are the steps in detail:
||\begin{align}\color{red} {-3x^3y^4} (\color{blue} {4xy^2}\color{green} {+2xy}) &= (\color{red} {-3x^3y^4}\times \color{blue} {4xy^2}) + (\color{red} {-3x^3y^4}\times \color{green} {2xy}) \\ &= -12x^{4}y^{6}+(-6x^4y^5)\\&=-12x^4y^6-6x^4y^5\end{align}||
When multiplying a polynomial by a polynomial, apply the distributive property of multiplication over addition by multiplying each of the terms in the first polynomial by each of the terms in the second polynomial.
For each multiplication, make sure to multiply the coefficients together.
For each multiplication, make sure to add the exponents of identical variables.
Don’t forget to put brackets around each polynomial.
Let the first polynomial be |-3x^3y^4+y| and the second polynomial be |4xy^2+2xy.| Begin the multiplication by placing the two polynomials in brackets:
||(-3x^{3}y^{4} + y){(4xy^{2} + 2xy)}||
Apply the distributive property of multiplication over addition, and multiply each term of the first polynomial by each term of the second polynomial.
Here are the steps in detail:
||(-3x^{3}y^{4} \times{4xy^{2}}) + (-3x^{3}y^{4}\times {2xy}) + (y\times {4xy^{2}}) + (y\times {2xy})||
||=(-12x^{4}y^{6}) + (-6x^{4}y^{5}) + (4xy^{3}) + (2xy^{2})||
The answer is: |-12x^{4}y^{6} - 6x^{4}y^{5} + 4xy^{3} + 2xy^{2}.|
When one polynomial is multiplied by another polynomial, each term of the first polynomial must be multiplied by each term of the second polynomial.
||\begin{align} &(-3x^{3}y^{4} + 1) {(4xy^{2} + 2xy - 9x + 2y)} \\\\ =\ &(-3x^{3}y^{4}\times 4xy^{2}) +(-3x^{3}y^{4}\times {2xy}) + (-3x^{3}y^{4}\times {-9x}) + (-3x^{3}y^{4}\times {2y})\\ &+ (1\times {4xy^{2}}) + (1\times {2xy}) + (1\times {-9x}) + (1\times {2y})\\ \\ =\ &(-12x^{4}y^{6}) + (-6x^{4}y^{5}) + (27x^{4}y^{4}) + (-6x^{3}y^{5}) \\ &+ (4xy^{2}) + (2xy) + (-9x) + (2y)\\ \\ =\ &-12x^{4}y^{6} - 6x^{4}y^{5} + 27x^{4}y^{4} - 6x^{3}y^{5} + 4xy^{2} + 2xy - 9x + 2y\end{align}||
Algebraic expressions can be multiplied using a visual method called algebra tiles.
Multiplying a constant term and a monomial using algebra tiles
Let the constant term be |3| and the monomial be |x.| Multiply |3\times x.| The multiplication is represented as follows:
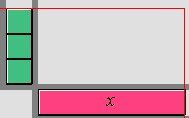
The three green boxes represent the constant term |3| and the pink rectangle represents the monomial |x.|
Multiply each term in the column by each term in the row. The product is represented by the area bounded by the rectangle.
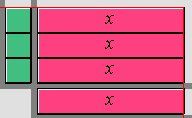
Since the rectangle is formed by three monomials |x,| the answer is |3x.|
Multiplying two monomials using algebra tiles
Let one monomial be |x| and the other be |x|. Multiply |x\times x.| The multiplication is represented as follows:

The two pink rectangles represent the monomials |x.|
Multiply each term in the column by each term in the row. The product is represented by the area bounded by the rectangle.
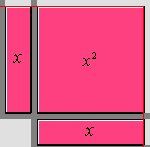
Since the rectangle is formed by the combination of two monomials |x,| the answer is |x^2.|
Multiplying a monomial and a binomial using algebra tiles
Let the monomial be |x| and the binomial be |(y + 2).| Multiply |x(y + 2).| The multiplication is represented as follows:
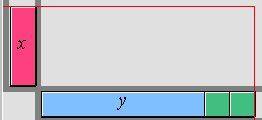
The column represents the monomial |x| and the row represents the polynomial |(y + 2),| where the blue rectangle represents the variable |y| and the two green squares represent two units |(+2).|
Multiply each term in the column by each term in the row. The product is represented by the area bounded by the rectangle.

Since the rectangles is formed by the combination of variables |x| and |y,| and by two monomials |x,| the answer is |xy + 2x.|
Multiplying two polynomials using algebra tiles
Let the polynomials be |(x + 1)| and |(x + 3).| Multiply |(x + 1)(x + 3).| The multiplication is represented as follows:

The column represents the polynomial |(x + 1),| where the variable |x| is represented by the pink rectangle and the number 1 is represented by the green square. The row represents the polynomial |(x + 3),| where the pink rectangle represents the variable |x| and the three green squares represent the number |3.|
Multiply each term in the column by each term in the row. The product is represented by the area bounded by the rectangle.
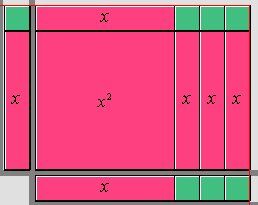
The answer is: |x^{2} + 4x + 3.|