Content code
m1472
Slug (identifier)
proofs-in-analytic-geometry
Parent content
Straight Lines and Half-Planes
Grades
Secondary IV
Secondary V
Topic
Mathematics
Tags
analytic geometry
proof
Cartesian plane
conjecture
QED
geometry
statements
assertions
prove
demonstrate
assert
conclusion
Content
Contenu
Content
Corps

In mathematics, a proof is defined as a sequence of logically related mathematical statements that prove a line of reasoning or a result.

Corps

Just like in classic geometry, proofs are used in analytic geometry to demonstrate the truth of a given statement. Some points to remember:

  • To produce a good proof in analytical geometry, you need to graph the proposition at hand on a Cartesian plane.

  • It is very important to use a minimum number of variables to label the important points on the figure. It's best to stay close to the axes.

  • The hypothesis must be clearly stated. The hypothesis consists of all the information in the proposition that is accepted as true and can be used for the proof.

  • The conclusion (what you want to prove) must be clearly stated.

  • Don't hesitate to look up any words that are complicated.

  • A number of analytic geometry tools may be useful. Before starting to write a proof, keep in mind the tools that will be used.

  • Don't hesitate to make a rough copy of the proof.

  • Make the proof as clear as possible so that someone else can read and validate it.

Here is an example of a proof in analytic geometry:

Prove that, in a right triangle, the midpoint of the hypotenuse is equidistant from the triangle's three vertices.

Image
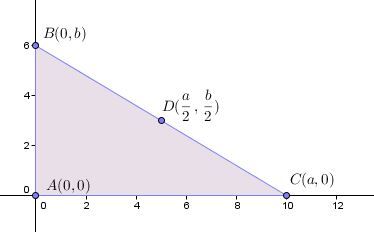
Triangle.
Corps

The word "equidistant" means "the same distance away", so the goal is to prove that the midpoint of the hypotenuse is the same distance away from all the vertices of a right triangle.

The proof is as follows:

Hypothesis:

Conclusion:

|\triangle ABC| is right-angled at |A|
|D| is the midpoint of |\overline {BC}|

|D| is equidistant from the three vertices of triangle |ABC.|

Statements:

Justifications:

The coordinates of |D| are |(\dfrac{a}{2},\dfrac{b}{2}).|

||\begin{align}(x_m,y_m)&=\left(\dfrac{x_2+x_1}{2},\dfrac{y_2+y_1}{2}\right)\\[3pt]&=\left(\dfrac{0+a}{2},\dfrac{b+0}{2}\right)\\[3pt]&=\left(\dfrac{a}{2},\dfrac{b}{2}\right)\end{align}||

||\text{dist}(D,C)=\text{dist}(D,B)||

||\begin{align}\text{dist}(D,C)&=\sqrt{\left(\dfrac{a}{2}-a\right)^2+\left(\dfrac{b}{2}-0\right)^2}\\[3pt]&=\sqrt{\left(\dfrac{-a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2}\\[3pt]&=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,B)&=\sqrt{\left(\dfrac{a}{2}-0\right)^2+\left(\dfrac{b}{2}-b\right)^2}\\[3pt]&=\sqrt{\left(\dfrac{a}{2}\right)^2+\left(\dfrac{-b}{2}\right)^2}\\[3pt]&=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\end{align}||

||\text{dist}(D,C)=\text{dist}(D,A)||

||\begin{align}\text{dist}(D,C)&=\sqrt{\left(\dfrac{a}{2}-a\right)^2+\left(\dfrac{b}{2}-0\right)^2}\\[3pt]&=\sqrt{\left(\dfrac{-a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2}\\[3pt]&=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,A)&=\sqrt{\left(\dfrac{a}{2}-0\right)^2+\left(\dfrac{b}{2}-0\right)^2}\\[3pt]&=\sqrt{\left(\dfrac{a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2}\\[3pt]&=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\end{align}||

|D| is equidistant from the three vertices of triangle |ABC.|

||\begin{gather}\text{dist}(D,C)=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,B)=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,A)=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}}\\[10pt]\text{dist}(D,C)=\text{dist}(D,B)=\text{dist}(D,A)\end{gather}||
Remove audio playback
No