When a transversal intersects one or more straight lines, it forms pairs of angles which have common properties.
In some cases, when two parallel lines are intersected by a transversal, specific pairs of angles are congruent (isometric).
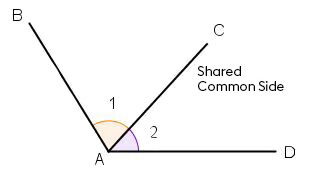
Adjacent angles are angles which have the same vertex, a common side, and are located on either side of this common side.
Therefore, the adjacent angles are “neighbouring” angles. They must be next to each other (have one side in common) and share the same vertex to qualify as adjacent.
Angles 1 |(\angle BAC)| and 2 |(\angle CAD)| below are adjacent angles since they have the same vertex |(A)| and they share a common side |(\overline{AC})|.
Complementary angles are angles where the sum of the measurements is equal to 90°.
When the sum of the measurements of two angles has a value of 90°, the angles are complementary.
||m\angle 1 + m\angle 2 + ... = 90^\circ||
To find one of two angles when only one of the measurements is given, simply subtract the value of the given angle from 90° to find the missing measurement.
Angles 1 |(\angle BAC)| and 2 |(\angle CAD)| are complementary since they form a right angle together.
Even if the angles are not adjacent, they can be complementary if the sum of their measurements equals 90°.
Supplementary angles are angles whose sum of their measurements is equal to 180°.
When the sum of the two angles’ measurements has a value of 180°, they are called supplementary angles.
||m\angle 1 + m\angle 2 + ... = 180^\circ||
To find one of two angles when only one of the measurements is given, simply subtract the given angle from 180°.
Angles 1 and 2 are supplementary since they form a straight angle together.
Even if the angles are not adjacent, they can be supplementary if the sum of their measurements equals 180°.
Vertically Opposite Angles are congruent angles which have a common vertex and the sides of one are the extension of the sides of the other.
Vertically opposite angles are composed of two straight lines which resemble the letter X.
Angles 1 and 3 are vertically opposite angles just like angles 2 and 4.
Thus:
||m\angle 1 = m\angle 3||
||m\angle 2 = m\angle 4||
Corresponding angles do not have the same vertex but are located on the same side of the transversal, one inside the lines being intersected by a transversal, and the other outside the lines.
Corresponding angles are isometric if the two lines intersected by the transversal are parallel.
Thus, the condition of parallel lines is essential to confirm the corresponding angles are congruent (isometric).
In the drawing below, the horizontal lines are parallel and they are cut by a transversal.
Thus:
||\begin{align} m\angle 1 & = m\angle 5 \\
m\angle 3 & = m\angle 7\\
m\angle 2 & = m\angle 6 \\
m\angle 4 & = m\angle 8 \end{align}||
In the case of a line intersecting two straight lines, if two corresponding angles are congruent, then the lines being cut by the transversal are parallel.
Alternate interior angles
-
do not have the same vertex,
-
are located on either side of the transversal, and
-
are located inside the lines being cut by the transversal.
Alternate Interior angles are congruent if the two lines intersected by the transversal are parallel.
Thus, it is important that the straight lines are parallel to determine angle congruency based on the information provided by the context.
In the drawing below, the horizontal lines are parallel.
Thus:
||\begin{align} m\angle 1 & = m\angle 4 \\
m\angle 2 & = m\angle 3 \end{align}||
In the case of a line intersecting two other lines, if two alternate interior angles are congruent, then the lines being cut by a transversal are parallel.
Alternate exterior angles
-
do not have the same vertex,
-
are located on either side of a transversal, and
-
are located outside the lines intersected by the transversal.
Alternate exterior angles are congruent if the two lines intersected by the transversal are parallel.
Conversely, if the two lines that are cut by a transversal are not parallel, then the angles are not congruent.
In the drawing below, the two horizontal lines are parallel.
Thus,
||\begin{align} m\angle 1 & = m\angle 3 \\
m\angle 2 & = m\angle 4 \end{align}||
In the case of a line intersecting two other lines, if two alternate exterior angles are congruent, then the lines intersected by a transversal are parallel.
It is possible to use the properties of angles to find the missing measurement.
What are the measurements of angles 2, 3, 5, and 8 in the drawing below if we know the following:
-
|d_1 \mid \mid d_2|,
-
|m\angle 1 = 122^\circ |?
Thus,
||\begin{align} m\angle 2 &= 58^\circ \ (\angle 1 \ \text{and} \ \angle 2 \ \text{are supplementary}) \\
m\angle 3 &= 58^\circ (\angle 2 \ \text{and} \ \angle 3 \ \text{are vertically opposite} )\\
m\angle 5 &= 122^\circ (\angle 1 \ \text{and} \angle 5 \ \text{are corresponding}) \\
m\angle 8 &= 122^\circ (\angle 1 \ \text{and} \ \angle 8 \ \text{are alternate exterior})\end{align}||