There are several different ways to express the solution set of an inequality.
Set builder notation involves writing both the inequality representing the situation and the number set that makes up the solution.
-
Integers that are greater than -3 and less than 7. |\to\ \{x \in \mathbb{Z} \mid -3 < x < 7 \}|
-
Natural numbers that are greater than or equal to 2. |\to\ \{x \in \mathbb{N} \mid x \ge 2 \}|
-
Real numbers that are greater than or equal to -5 and less than 6. |\to\ \{x \in \mathbb{R} \mid -5 \le x < 6 \}|
Single-variable inequalities can be plotted on a number line.
To start, draw the number line and plot the number of the inequality.
-
If the inequality sign also contains an equality |(\le, \ge)|, place a solid point |(\bullet)| to indicate that the endpoint is included in the solution.
-
If the inequality sign does not contain an equality |(<, >)|, place an empty point |(\circ)| to indicate that the endpoint is excluded from the solution.
Example of an inequality containing an equality
Consider the following inequality. ||\begin{align} 2x+5 &\le9 \\ 2x+5\color{red}{-5}&\le9\color{red}{-5} \\ 2x&\le4\\ \dfrac{2x}{\color{red}{2}} &\le\frac{4}{\color{red}{2}} \\ x &\le2 \end{align}||
In this example, a solid point must be placed on the number |2| since the inequality also includes an equality.
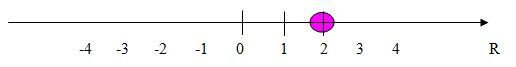
Afterwards, we must represent the inequality part of the solution (numbers less than or greater than). Since no set of numbers was specified at the start of the problem, the solution set is assumed to be made of real numbers. Therefore, there are an infinite number of solutions for this inequality.
In this example, the solutions are all numbers less than or equal to |2.| So |2,| |1,| |\dfrac{1}{2},| |\dfrac{1}{4},| |0,| |-1,| |-2, …| are all solutions to the inequality.
To represent this, draw a line to indicate all the solutions to the inequality.

Example of an inequality without an equality
||\begin{align} 35-3x &< 7+4x \\ 35-3x \color{red}{+3x} &< 7+4x \color{red}{+3x} \\35 &<7+7x \\35 \color{red}{-7} &<7+7x \color{red}{-7} \\28 &< 7x \\ \dfrac{28}{\color{red}{7}} &< \dfrac{7x}{\color{red}{7}} \\ 4&< x \end{align}||
Note: |4<x| is the same as |x>4.|
Since there is no equality, an empty point indicates the endpoint of the inequality.

Examples of inequalities in the set of integers
|\{x \in \mathbb{Z} \mid -2 < x < 3 \}|
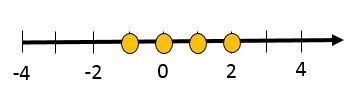
|\{x \in \mathbb{Z} \mid -2 \le x \le 3 \}|

It is also possible to express the solution-set of an inequality by listing the elements in curly brackets or using interval notation.
-
Curly brackets can only be used when the solution set is made of integers. Simply list the possible solutions.
|\{x \in \mathbb{Z} \mid -2 < x < 3 \}| |\to| |\{-1, 0, 1, 2 \}|
|\{x \in \mathbb{Z} \mid -2 \le x \le 3 \}| |\to| |\{-2, -1, 0, 1, 2, 3 \}|
|\{x \in \mathbb{Z} \mid x \le 3 \}| |\to| |\{..., -2, -1, 0, 1, 2, 3 \}|
-
Interval notation must be used when the solution set is part of the real numbers. The interval includes all the numbers between the two endpoints. It is important to pay attention to if an endpoint is included (bracket) or excluded (parenthesis). Infinity |(\infty)| is never included in an interval.
|\{x \in \mathbb{R} \mid -5 \le x < 6 \}| |\to| |[-5, 6[|
|\{x \in \mathbb{R} \mid x < 4 \}| |\to| |]-\infty, 4[|
|\{x \in \mathbb{R} \mid x \ge 6 \}| |\to| |[6, +\infty[|