The substitution method is a method for algebraically solving a system of equations where one equation has the form |y = ax + b| and the other has the form |ax + by = c|.
The method of solving a system by substitution is generally preferred when a variable is isolated in only one of the two equations. In other words, when the system has the following form. ||\begin{cases}y=a_1x+b_1 \\ a_2x+b_2y=c \end{cases}||
The substitution method consists of replacing the isolated variable with an equivalent algebraic expression. The equivalent expression is substituted into the equation where the variable is not isolated. Visually, it can be represented like this.
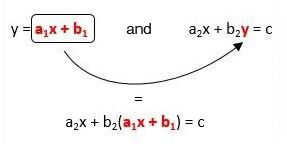
It is possible to use this method even if there isn’t an isolated variable in either equation. Just carry out some algebraic manipulations and isolate a variable in one of the equations before using the substitution method.
It does not have to be the dependent variable (usually denoted by |y|) that is isolated in one equation and substituted into the other. The substitution method works with any isolated variable, regardless if it is the dependent or independent variable. It just needs to be the same variable that is isolated in one equation and substituted in the other.
To algebraically solve a system of equations using the substitution method, follow these steps.
-
For a word problem, define the variables and translate the situation into a system of equations.
-
Isolate a variable in one of the two equations, if necessary.
-
Replace this variable in the second equation with the corresponding algebraic expression, in order to form a single-variable equation.
-
Solve the equation.
-
Substitute the value found in step 4 into one of the initial equations to find the value of the second variable.
-
Verify the answer by substituting the values obtained for the variables into each of the initial equations.
Consider the following system of equations.
||\begin{cases}y = -8x - 6 \\ 4x+3y=42 \end{cases}||
-
For a word problem, define the variables and translate the situation into a system of equations
As the system is already provided, this step is not necessary. -
Isolate a variable in one of the two equations, if necessary
This step has already been completed since the variable |y| is isolated in the first equation. -
Replace this variable in the second equation with the corresponding algebraic expression to form a single-variable equation
||y = \color{red}{-8x - 6}\ \ \text{and}\ \ 4x+3\color{red}{y} = 42\\ \Rightarrow 4x+3(\color{red}{-8x - 6}) = 42|| -
Solve the equation
||\begin{align}4x+3(-8x-6)&=42 \\
4x-24x-18&=42 \\
-20x-18\color{red}{+18}&=42\color{red}{+18} \\
-20x&=60\\
-20x\color{red}{\div -20}&=60\color{red}{\div -20}\\
x&=-3\end{align}|| -
Substitute the value found in step 4 into one of the initial equations to find the value of the second variable
It is easier to use the first equation since the variable |y| is already isolated.
||\begin{align}y& = -8x - 6\\
y &= -8(\color{red}{-3}) - 6\\
y &= 24 - 6\\
y &= 18\end{align}|| -
Verify the answer by substituting the values obtained for the variables into each of the initial equations.
||\begin{align} y&=-8x-6 & 4x+3y&=42\\
(18)&=-8(-3)-6 & 4(-3)+3(18)&=42\\
18&=24-6 & -12+54&=42\\
18&=18 & 42&=42\end{align}||
Since the values satisfy the two equations, the system’s solution is the point |(-3,18)|.
Consider the following system of equations.
||\begin{cases}2a + 3b = 5\\ \displaystyle b = \frac{a + 5}{3}\end{cases}||
-
For a word problem, define the variables and translate the situation into a system of equations
Since the system is already provided, this step is not necessary. -
Isolate a variable in one of the two equations, if necessary
This step has already been completed since the variable |y| is isolated in the first equation. -
Replace this variable in the second equation with the corresponding algebraic expression to form a single-variable equation ||b = \color{red}{\dfrac{a + 5}{3}}\ \ \text{and}\ \ 2a + 3\color{red}{b} = 5\\ \Rightarrow 2a + 3\left(\color{red}{\dfrac{a + 5}{3}}\right) = 5||
-
Solve the equation ||\begin{align}2a + 3\left({\dfrac{a}{3}} + \dfrac{5}{3}\right) &= 5\\ \\ 2a + {\dfrac{3a}{3}} + \dfrac{15}{3} &= 5\\ \\ 2a + a + 5 &= 5\\ \\ 3a + 5 &= 5\\ \\ 3a &= 0\\ \\ a &= 0\end{align}||
-
Substitute the value found in step 4 into one of the initial equations to find the value of the second variable||\begin{align} b &= \dfrac{a + 5}{3}\\
b &= \dfrac{\color{red}{0} + 5}{3}\\
b& = \dfrac{5}{3}\end{align}|| -
Verify the answer by substituting the values obtained for the variables into each of the initial equations||\begin{align} 2a+3b&=5 & b&={\dfrac{a + 5}{3}}\\ 2(0)+3\left({\dfrac{5}{3}}\right)&=5 & \left({\dfrac{5}{3}}\right)&={\dfrac{(0)+5}{3}}\\ 0+5&=5 & {\dfrac{5}{3}}&={\dfrac{5}{3}}\\ 5&=5\end{align}||
Since the values satisfy the two equations, the solution to the system is the point |\left(0, \dfrac{5}{3}\right).|
Consider the following system of equations.
||\begin{cases}10x + 40y = 30 \\ -2 = -x - 4y \end{cases}||
-
For a word problem, define the variables and translate the situation into a system of equations
Since the system is already provided, this step is not necessary. -
Isolate a variable in one of the two equations, if necessary ||\begin{align}-2&=-x-4y\\
-2\color{red}{+x}&=-x\color{red}{+x}-4y\\
-2\color{red}{+2}+x&=-4y\color{red}{+2}\\
x&=2-4y\end{align}|| -
Replace this same variable in the second equation with the corresponding algebra expression to form a single-variable equation ||x = \color{red}{2 - 4y}\ \ \text{and}\ \ 10\color{red}{x} + 40y = 30\\
\Rightarrow 10(\color{red}{2 - 4y}) + 40y = 30|| -
Solve the equation ||\begin{align}10(2-4y)+40y&=30\\
20 - 40y + 40y &= 30\\
20\color{red}{-20} - 40y + 40y &= 30 \color{red}{-20}\\
-40y + 40y &= 10\\
0 &= 10\end{align}||
This answer is impossible. Therefore, there is no solution to this system of equations. To make sure, rewrite the two equations in the form |y = ax + b|. Note that the two equations have the same slope, but the |y|-intercepts are different; therefore, the two equations represent non-coinciding parallel lines.
||\begin{align}10x + 40y = 30 &\Rightarrow y = \frac{-1}{4}x + \frac{3}{4}\\
\\
x = 2 - 4y &\Rightarrow y = \frac{-1}{4}x - \frac{1}{2}\end{align}||
Pour valider ta compréhension à propos de la résolution de systèmes d'équations à l'aide de la méthode de comparaison, de réduction ou de substitution de façon interactive, consulte la MiniRécup suivante.
