The Cartesian plane is a plane surface defined by the intersection of two perpendicular number lines.
This system allows us, among other things, to locate points in the plane and to represent a relationship between two variables.
A Cartesian plane has several characteristics:
-
First, it is defined by having two perpendicular axes: the x-axis (|x|), which is horizontal and the y-axis (|y|), which is vertical.
-
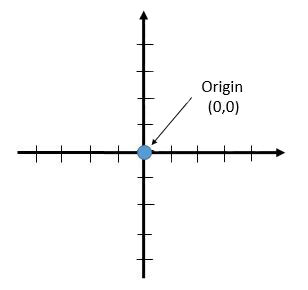
The two axes intersect at the origin, i.e. at the point |(0,0)|.
-
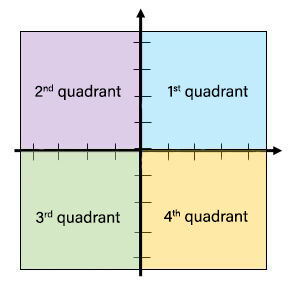
The Cartesian plane is then divided into four sections called quadrants.
The horizontal axis of a Cartesian plane is called the |x|-axis. This graduated axis is oriented from left to right in the Cartesian plane. It indicates the value of the independent variable in a relationship between two variables.
On the horizontal axis:
-
The numbers are positive to the right of the origin (zero).
-
The numbers are negative to the left of the origin (zero).
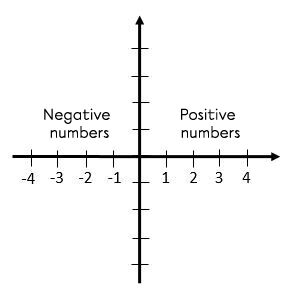
The vertical axis of a Cartesian plane is called the |y|-axis. This graduated axis is oriented from the bottom to the top of the Cartesian plane. It indicates the value of the dependent variable in a relationship between two variables.
On the vertical axis:
-
The numbers above the origin (zero) are positive.
-
The numbers below the origin (zero) are negative.

The origin of the Cartesian plane is the point where the perpendicular number lines intersect. This is indicated by the point |(0,0)|.
The quadrants correspond to the four regions delimited by the axes. The four quadrants are numbered counterclockwise, as seen in the following Cartesian plane.
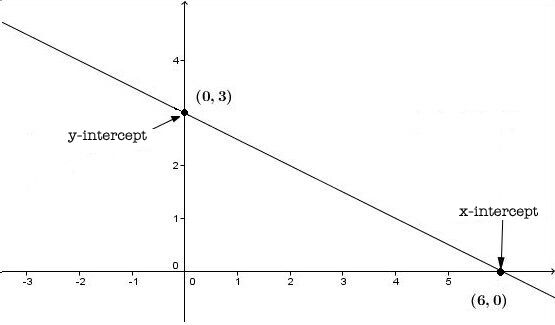
The x-intercept is the value of the independent variable |(x)| when the dependent variable |(y)| is zero. In other words, this is the place on the graph where the line crosses the x-axis.
The y-intercept is the value of the dependent variable |(y)| when the independent variable |(x)| is zero. In other words, this is the place on the graph where the line crosses the y-axis.
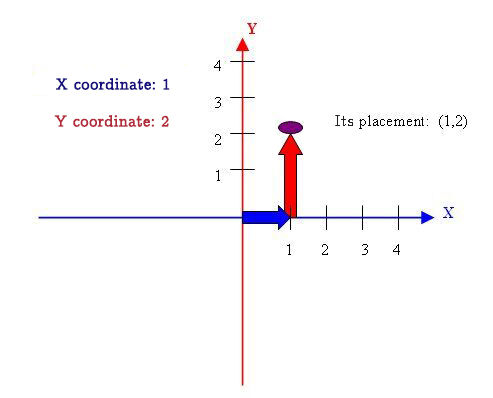
The graduation of the axes on the Cartesian plane makes it possible to locate points in one or the other four quadrants. The position of a point is given by an ordered pair of numbers called the coordinates |(x, y)|. The first number of the coordinate corresponds to the horizontal position of the point (its value on the |x|-axis), while the second number corresponds to its vertical position (its value on the |y|-axis).
So, when locating a point in a Cartesian plane, always start by identifying the value of the horizontal axis, the |x| coordinate, followed by the value of the vertical axis, the |y| coordinate. Then write the ordered pair in round brackets, separating it with a comma:
|\text{Ordered Pair}=(\text{Value of the horizontal axis}, \text{Value of the vertical axis})=(x,y)|
Use the following procedure to find the coordinates of a point on the Cartesian plane.
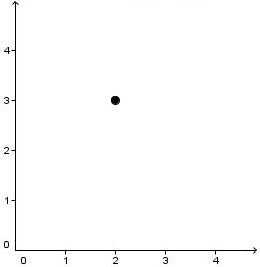
What are the coordinates of this point?
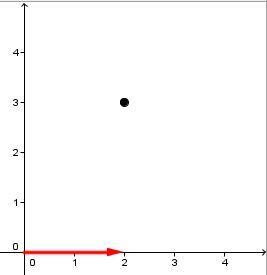
First, read the value of the horizontal axis, the |x|-axis. In this case, move two units to the right.
Next, read the value of the vertical axis, the |y|-axis. In this case, move three units upwards to get to the point.
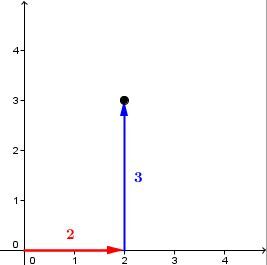
The coordinates of this point are |(2,3).|
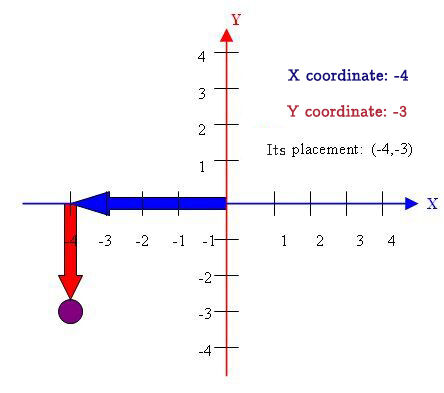
To locate a point in the Cartesian plane with the four quadrants, use the same technique as with quadrant one. However, it is necessary to take into account the positive and negative sign of the coordinates.