The distance from a point to a line is the length of the shortest possible segment connecting a point to a line.
To determine the distance of a point from a line, we measure the length of the perpendicular segment that joins the line to the point.
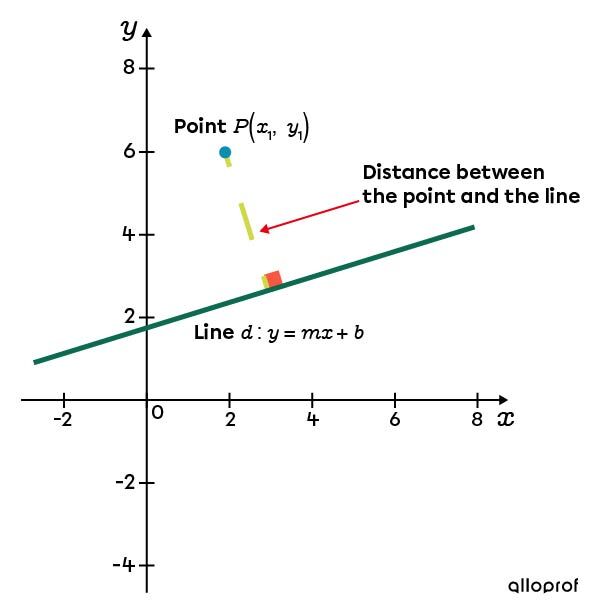
Given the equation of the line and the coordinates of the point, the distance between the two can be found by following these steps.
-
Draw a line passing through point |P| perpendicular to the given line.
-
Determine the slope of this line: it is the opposite inverse (negative reciprocal) of the slope of the line |d|.
-
Replace |x| and |y| with the coordinates of |P| to calculate the |y|-intercept of the perpendicular line.
-
Replace the found values of |m| and |b| to get the equation of the perpendicular line.
-
Use the comparison method to find the point of intersection between |d| and the perpendicular line (if necessary, see solving a system of equations).
-
Apply the formula for the distance between two points to find the distance between the point |P| and the line |d|.
What is the distance between the line |d| with the equation |y = -2x+7| and the point |P| with coordinates |(6,4)|?
The animation below shows the steps in detail.
These steps can be simplified by using a formula to calculate the distance between a point and a line.
Slope-intercept equation:
Given a point |P(x_1, y_1)| and a line |D| with the equation |y = mx + b|, use the following formula.
|d(D,P) = \displaystyle \frac{\mid mx_1 - y_1 + b \mid}{\sqrt{m^2 + 1}}|
Standard form equation:
Given a point |P(x_1,y_1)| and a line |D| with the equation |Ax + By + C = 0|, use the following formula.
|d(D,P) = \displaystyle \frac{\mid Ax_1 + By_1 + C \mid}{\sqrt{A^2 + B^2}}|
What is the distance between the line with equation |y = 3x – 4| and the point P with coordinates |(4 , -1)|?
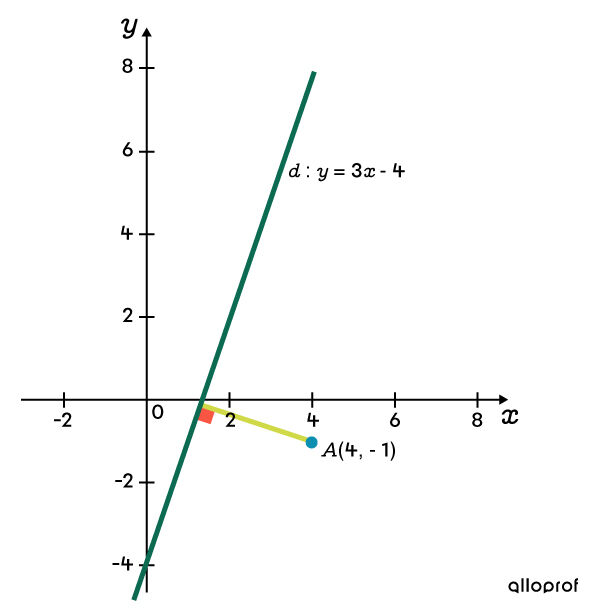
Since the line is written in the slope-intercept form, we will use the first formula. ||\begin{align} d &= \dfrac{\mid mx_1 - y_1 + b\mid}{\sqrt{m^2 + 1}} \\ d &= \dfrac{\mid (3\times 4) - (-1) + (-4)\mid}{\sqrt{3^2 + 1}} \\d &= \dfrac{\mid 12 + 1 - 4\mid}{\sqrt{9 + 1}} = \frac{\mid 9 \mid}{\sqrt{10}} \approx 2.85\ \text{units} \end{align}||
The exact same result can be obtained by using the other formula.
Transform the equation of the line into standard form: |0 = 3x – y - 4.| ||\begin{align} d &= \dfrac{\mid Ax_1 + By_1 + C \mid}{\sqrt{A^2 + B^2}} \\ d &= \dfrac{\mid (3\times 4) + (-1 \times -1) + (-4) \mid}{\sqrt{3^2 + (-1)^2}} \\ d &= \dfrac{\mid 12 + 1 - 4 \mid}{\sqrt{9 + 1}} \end{align}||
This gives the same result, i.e. approximately |2.85| units.