-
A division point of a segment is a point that divides the segment into two parts according to a given ratio. This ratio is between 0 and 1 inclusively.
-
The midpoint is a division point that separates the initial segment into 2 equal segments.
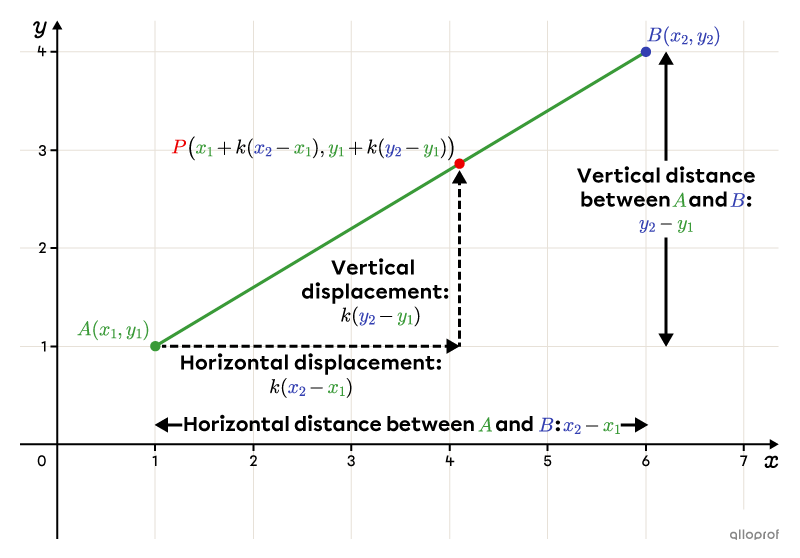
The coordinates of the division point |P| of segment |\overline{AB}| are given by the following formula:
||(x_{\small{P}},y_{\small{P}})=\big(x_1+k(x_2-x_1),y_1+k(y_2-y_1)\big)||
|A(x_1,y_1)| is the 1st endpoint (starting point).
|B(x_2,y_2)| is the 2nd endpoint.
|P(x_{\small{P}},y_{\small{P}})| is the division point.
|k| corresponds to the part-to-whole ratio.
In a way, one formula actually serves as 2: the first for the division point's x-coordinate: |x_{\small{P}}=x_1+k(x_2-x_1)| and the second for the y-coordinate: |y_{\small{P}}=y_1+k(y_2-y_1).|
The following explanation shows how to calculate |x_{\small{P}}.|
-
|x_2-x_1| corresponds to the horizontal distance between the 2 endpoints of the line segment.
-
|k(x_2-x_1)| gives the horizontal displacement from the starting point |(A)| to point |P.|
-
Since the starting point's x-coordinate is |x_1,| we can get the division point's x-coordinate |(x_{\small{P}})| by adding the horizontal displacement to |x_1.|
Note: The same reasoning applies to |y_{\small{P}}.|
Sometimes, the way the segment is divided is given using a part-to-whole ratio. Other times, it's given using a part-to-part ratio. Once you've determined the type of ratio provided, you can use the division point formula.
Consider the following segment |\overline{AB}.| Point |P| divides this segment into 2 parts |(\overline{AP}| and |\overline{PB}).| As a result, the total length of the segment corresponds to the sum of the parts |\overline{AP}| and |\overline{PB}.|
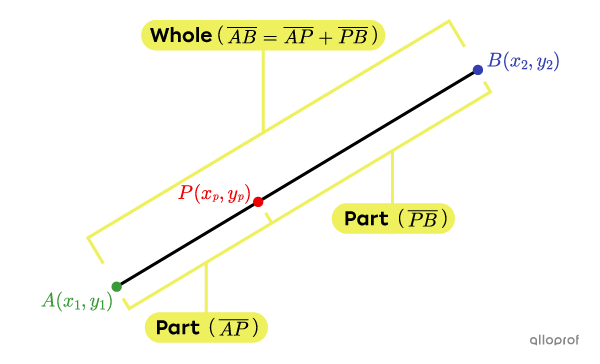
The Part-to-Whole Ratio |\boldsymbol{(k)}|
When point |P| divides a segment into a ratio that compares a part of the segment to the whole segment, it is called a part-to-whole ratio. This ratio is always expressed as a fraction.
In this case, the ratio is the |\boldsymbol{k}| value to be used in the division point formula. ||k=\dfrac{\text{m}\overline{AP}}{\text{m}\overline{AB}}||
The Part-to-Part Ratio
When point |P| divides a segment using a ratio that is given by comparing the 2 separate parts of the segment, it's called a part-to-part ratio.||\text{m}\overline{AP}\!:{\text{m}\overline{PB}}||In this case, the |k| value to use in the division point formula is as follows:||k=\dfrac{\text{m}\overline{AP}}{\text{m}\overline{AP}+\text{m}\overline{PB}}||
Special attention must be paid to the starting point of the segment, since this affects the ratio to be used |(k)| in the division point formula.
Sometimes, the starting point is not explicitly given. For example, if we say that |P| is located |\dfrac{3}{10}| of the way along segment |\overline{FG},| we can assume that |F| is the starting point.
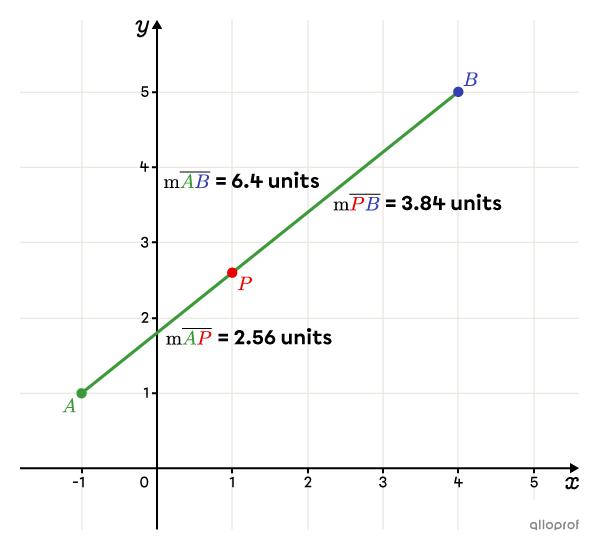
The Part-to-Whole Ratio |\boldsymbol{(k)}|
The part-to-whole ratio, expressed as a fraction, is as follows:||\begin{align}k&=\dfrac{\text{m}\overline{AP}}{\text{m}\overline{AB}}\\[3pt] &=\dfrac{\text{m}\overline{AP}}{\text{m}\overline{AP}+\text{m}\overline{PB}}\\[3pt] &=\dfrac{2.56}{2.56+3.84}\\[3pt] &=\dfrac{2.56}{6.4}\\[3pt] &=\dfrac{2}{5}\end{align}||In other words, the division point |(P)| is located at |\dfrac{2}{5}| along segment |\overline{AB}| from point |A.|
If we consider that |B| is the starting point of segment |\overline{BA},| then point |P| is instead located at |\dfrac{3}{5}| of segment |\overline{BA}| from |B.| Because |1-\dfrac{2}{5}=\dfrac{3}{5}.|
The Part-to-Part Ratio
The part-to-part ratio is as follows:||\text{m}\overline{AP}:\text{m}\overline{PB}=2.56:3.84||By reducing this ratio, we get a ratio of |2:3.|
This means that for every |2| parts of equal length in segment |\overline{AP},| there are 3 parts of the same length in segment |\overline{PB}.|
We can also say that point |P| divides segment |\overline{BA}| into a ratio of |3 : 2.|
In the following interactive animation, you can move the division point |\boldsymbol{\color{#ec0000}{P}}| and see the effect on the 4 possible ratios: the part-to-part ratio when |A| is the starting point and when |B| is the starting point, as well as the part-to-whole ratio when |A| is the starting point and when |B| is the starting point.
Consider points |A(4,6)| and |B(8,12).| We want to find the coordinates of point |P| located |\dfrac{3}{4}| of the way along line segment |\overline{AB}| from point |A.|
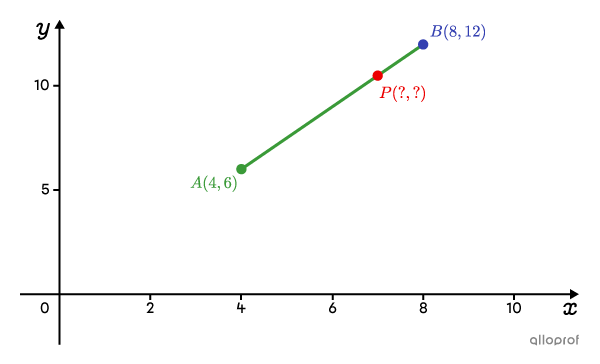
Here, |(x_1,y_1)=(4,6)| and |(x_2,y_2)=(8,12).|
Furthermore, the ratio given in the statement is a part-to-whole ratio. Therefore, |k=\dfrac{3}{4}| and the starting point is point |A.|
This means we can apply the division point formula. You can either apply it all at once, or calculate the |x| and |y| coordinates of the division point separately as we will do here.
We start by calculating the x-coordinate of point |P,| which we denote |x_{\small{P}}.|||\begin{align} x_{\small{P}} &= x_1 + k(x_2-x_1)\\[3pt]&= 4 + \dfrac{3}{4}(8-4)\\[3pt]&= 4 + \dfrac{3}{4}(4)\\[3pt]&= 4 + 3\\[3pt] &= 7\end{align}||Next, we calculate the y-coordinate of point |P,| which we denote |y_{\small{P}}.|
||\begin{align} y_{\small{P}} &= y_1 + k(y_2-y_1)\\[3pt]&= 6 + \dfrac{3}{4}(12-6)\\[3pt]&= 6 + \dfrac{3}{4} (6)\\[3pt]&= 6 + 4.5\\[3pt] &= 10.5\end{align}||
Answer: The division point is |P(7, 10.5).|
|A(5,-3)| and |B(10,6)| are the endpoints of a line segment. We want to find the coordinates of point |P| that divides the segment into a ratio of |3:2,| starting from point |B.|
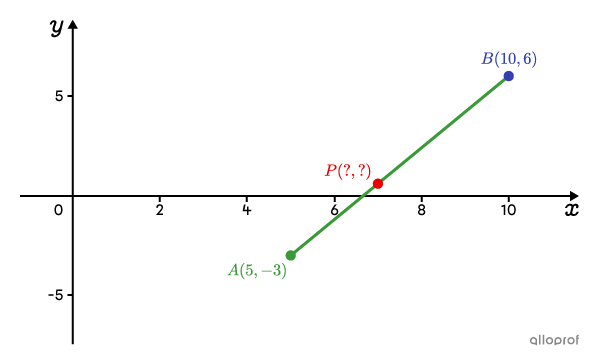
The ratio mentioned in the statement is a part-to-part ratio. It must therefore be transformed into a part-to-whole ratio.
In this example, |\text{m}\overline{BP}:\text{m}\overline{PA}=3:2.| We can calculate the value of |k| as follows: ||k = \dfrac{3}{3+2} = \dfrac{3}{5}||It must also be noted that the starting point is point |B| and not point |A.| Therefore, we must use the division point formula with |B(x_1,y_1)=(10,6)| and |A(x_2,y_2)=(5, -3).|||\begin{align}(x_{\small{P}},y_{\small{P}})&=\big(x_1+k(x_2-x_1),\ y_1+k(y_2-y_1)\big)\\[3pt] &=\left(10+\dfrac{3}{5}(5-10),\ 6+\dfrac{3}{5}(-3-6)\right)\\[3pt] &=\left(10+\dfrac{3}{5}(-5),\ 6+\dfrac{3}{5}(-9)\right)\\[3pt] &=\left(10-3,\ 6-5.4\right)\\[3pt] &=\left(7, 0.6\right) \end{align}||
Answer: The coordinates of point |P| are therefore |\left(7, 0.6\right).|
If the division point of a segment is known along with one of its 2 endpoints, you can use the division point formula to find the coordinates of the other endpoint. To do so, simply form one equation with the |x| coordinate and another with the |y| coordinate.
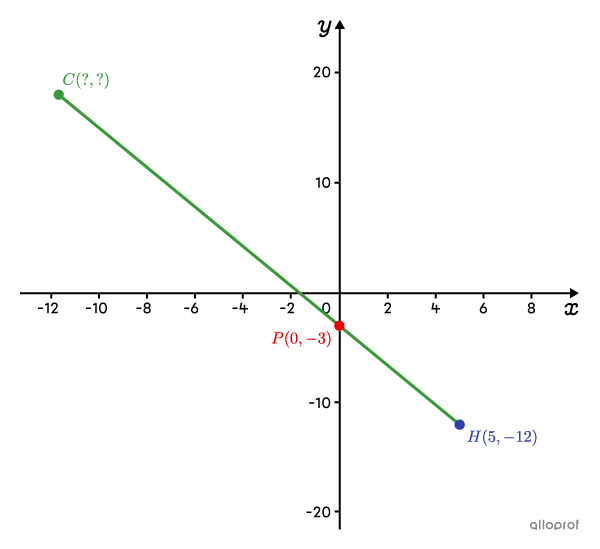
In the following Cartesian plane, we find the points |C,| |P(0,-3)| and |H(5,-12).| These 3 points are aligned.
Point |P| divides segment |\overline{CH}| into a ratio of |7:3| from point |C.|
What are the coordinates of point |C|?
Le point |P| partage le segment |\overline{CH}| dans un rapport |7:3| à partir du point |C.|
Quelles sont les coordonnées du point |C|?
Before starting any calculations, it's important to note that the ratio given is a part-to-part ratio. It must therefore be transformed into a part-to-whole ratio.
In this example, |\text{m}\overline{CP}:\text{m}\overline{PH}=7:3.| We can calculate the |k| value as follows:||k = \dfrac{7}{7+3} = \dfrac{7}{10}||So, the part-to-whole ratio is ||k =\dfrac{7}{10}|| when |C| is the starting point.
We now form 2 equations: one with the x-coordinates, to find the value of |x_1,| and the other with the y-coordinates, to find |y_1.| We replace |x_{\small{P}}| and |y_{\small{P}}| with |0| and |-3,| and also |k| with |\dfrac{7}{10}.| We also replace |x_2| and |y_2| with the coordinates of the endpoint |H,| that is, |5| and |-12| respectively. Finally, we solve the 2 equations.
||\begin{align} x_{\small{P}}&=x_1+k(x_2-x_1)\\[3pt]0&=x_1+\dfrac{7}{10}(5-x_1)\\[3pt] 0&=x_1+3.5-0.7x_1\\[3pt] \color{#ec0000}{\dfrac{\color{black}{-3.5}}{0.3}}&=\color{#ec0000}{\dfrac{\color{black}{0.3x_1}}{0.3}}\\[3pt] -\dfrac{35}{3}&=x_1\end{align}||
||\begin{align}y_{\small{P}}&=y_1+k(y_2-y_1)\\[3pt]-3&=y_1+\dfrac{7}{10}(-12-y_1)\\[3pt] -3 &=y_1-8.4-0.7y_1\\[3pt] \color{#ec0000}{\dfrac{\color{black}{5.4}}{0.3}}&=\color{#ec0000}{\dfrac{\color{black}{0.3y_1}}{0.3}}\\[3pt] 18&=y_1\end{align}||
Answer: The coordinates of point |C| are |\left(-\dfrac{35}{3},18\right).|
Note: It is possible to assume that the division point is located at |\dfrac{3}{10}| of the line segment |\overline{HC}| from the point |H,| because |\dfrac{10}{10}-\dfrac{7}{10}=\dfrac{3}{10}.| In this case, |k=\dfrac{3}{10},| |(x_1,y_1)=(5,-12),| and we are looking for |(x_2, y_2).| Here is proof that we get the same answer in the end.
||\begin{align}x_{\small{P}}&=x_1+k(x_2-x_1)\\[3pt] 0&=5+\dfrac{3}{10}(x_2-5)\\[3pt] 0&=5+0.3x_2-1.5\\[3pt] -0.3x_2&=3.5\\[3pt]x_2&=\dfrac{3.5}{-0.3}\\[3pt] x_2&=\dfrac{-35}{3}\end{align}||
||\begin{align}y_{\small{P}}&=y_1+k(y_2-y_1)\\[3pt]-3&=-12+\dfrac{3}{10}(y_2--12)\\[3pt] -3&=-12+0.3y_2+3.6\\[3pt]-0.3y_2&=-5.4\\[3pt] -3y_2&=-54 \\[3pt]y_2&=18\end{align}||
||\text{Midpoint} = \left( \dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2} \right)||where
|(x_1,y_1)| and |(x_2,y_2)| are the coordinates of 2 endpoints of a line segment.
In the division point formula, we had to do |x_2| minus |x_1| and |y_2| minus |y_1,| whereas in the midpoint formula, we must do |x_1| plus |x_2| and |y_1| plus |y_2.|
In fact, you don't even need to memorize the midpoint formula. Simply learn the more versatile division point formula and replace |k| with |\dfrac{1}{2}.|
Here's proof that the midpoint formula is indeed obtained from the division point formula.||\begin{align}(x_{\small{P}},y_{\small{P}})&=\big(x_1+\boldsymbol{\color{#3a9a38}k}(x_2-x_1),y_1+\boldsymbol{\color{#3a9a38}k}(y_2-y_1)\big)\\[3pt] \text{Midpoint}&=\left(x_1+\boldsymbol{\color{#3a9a38}{\dfrac{1}{2}}}(x_2-x_1),y_1+\boldsymbol{\color{#3a9a38}{\dfrac{1}{2}}}(y_2-y_1)\right)\\[3pt] &=\left(x_1+\dfrac{1}{2}x_2-\dfrac{1}{2}x_1,y_1+\dfrac{1}{2}y_2-\dfrac{1}{2}y_1\right) \\[3pt]&=\left(\dfrac{1}{2}x_1+\dfrac{1}{2}x_2,\dfrac{1}{2}y_1+\dfrac{1}{2}y_2\right) \\[3pt] &=\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right) \end{align}||
In the division point formula, we need to calculate |x_2 - x_1| and |y_2-y_1,| because we're using the notion of distance between the starting point and the endpoint.
For midpoint, we can see the calculation |\dfrac{x_1+x_2}{2}| as being the average between the two x-coordinates, or the average of the two. The same applies to the y-coordinates.
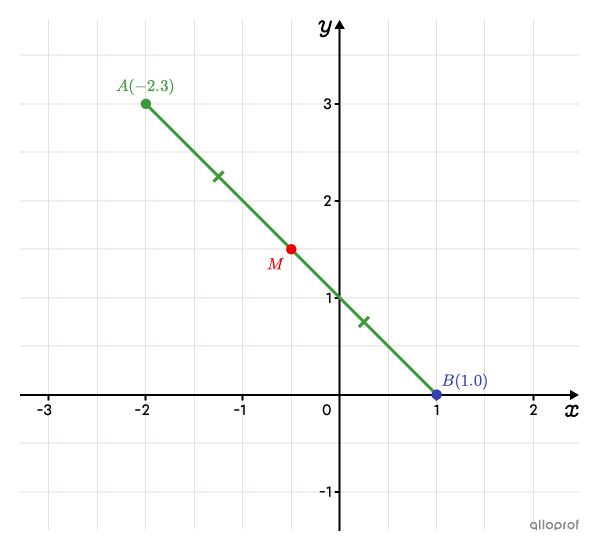
What are the coordinates of the midpoint of the segment formed by points |A(-2, 3)| and |B(1, 0)|?
||\begin{align} \text{Midpoint}&=\left(\dfrac{x_{1}+x_{2}}{2},\dfrac{y_{1}+y_{2}}{2}\right)\\[3pt]&=\left(\dfrac{-2+1}{2},\dfrac{3+0}{2}\right)\\[3pt]&=\left(-0.5, 1.5\right)\end{align}||
If the midpoint of a segment and one of its 2 endpoints are known, it's possible to use the midpoint formula to find the coordinates of the other endpoint. To do this, simply form one equation with the x-coordinate and another with the y-coordinate.
The coordinates of the midpoint |(M)| of segment |\overline{CD}| are |(12.5,-4).| What are the coordinates of point |C| given that those of point |D| are |(8,1)|?
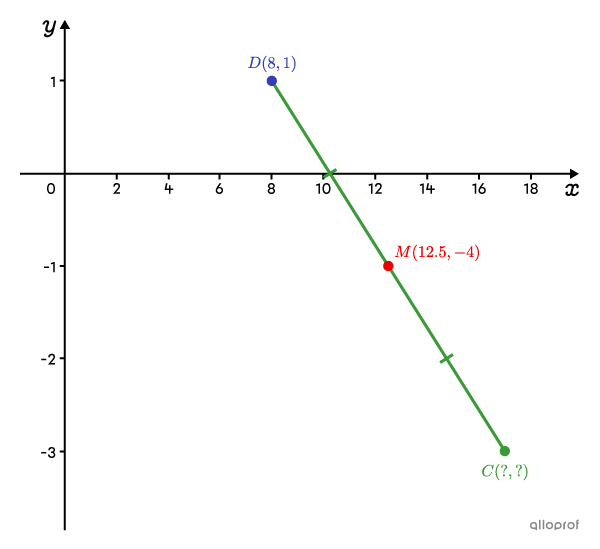
In the midpoint formula, we replace the "midpoint" with the coordinates |(12.5,-4).| We also replace |x_2| and |y_2| with the coordinates of the endpoint |D,| or |8| and |1| respectively.||\begin{align} \text{Midpoint}&=\left(\dfrac{x_{1}+x_{2}}{2},\dfrac{y_{1}+y_{2}}{2}\right)\\[3pt](12.5,-4)&=\left(\dfrac{x_1+8}{2},\dfrac{y_1+1}{2}\right)\end{align}||From here, we form 2 equations: one with the x-coordinates, which will allow us to find the value of |x_1,| and the other with the y-coordinates, which will allow us to find |y_1.|||\begin{align}12.5&=\dfrac{x_1+8}{2}&-4&=\dfrac{y_1+1}{2}\\[3pt]25&=x_1+8&-8&=y_1+1\\[3pt]17&=x_1&-9&=y_1\end{align}||
Answer: Therefore, the coordinates of point |C| are |(17,-9).|