The Law of Sines is a formula relating the ratios of the angles’ sines to their opposite side measurements. It is valid for all triangles.
The law of sines makes it possible to find the measurement of any triangle’s side or angle. To use it, the measurement of an angle, its opposite side, and another side or angle must be known.
The law of sines takes the following form: ||\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}||
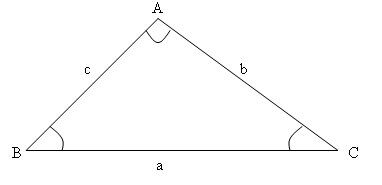
Note: The formula can also be written as follows: ||\dfrac{\sin A}{a}=\dfrac{\sin B}{b} = \dfrac{\sin C}{c}||
The sine law is used when the measurement of an angle and its opposite side are known, in addition to any other side (left) or angle (right) value of the triangle.
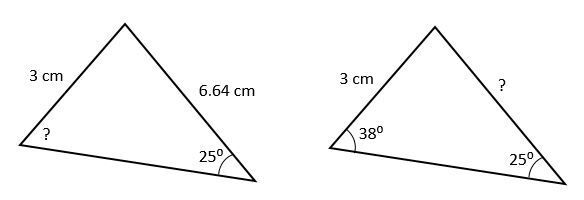
In short, a complete pair (side, angle) is needed.
What is the measurement of the side opposite the 35° angle?
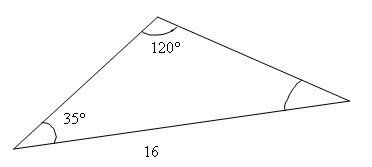
First, use the equation relating the side opposite to the 35° angle with the given information, as follows:
||\begin{align} \frac{16}{\sin120^{\circ}}&=\frac{x}{\sin35^{\circ}}\\\\ \Rightarrow\ x&=\frac{16\sin35^{\circ}}{\sin120^{\circ}}\\ x&=10{.}6 \end{align}||
Thus, the side opposite the 35º angle measures 10.6 units.
Situation with an obtuse angle
What is the measurement of the angle opposite the side |\overline{XZ}|?
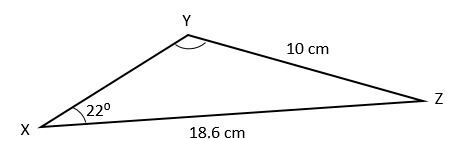
The law of sines is used to find the missing value:
||\begin{align} \frac{10}{\sin 22^{\circ}} &= \dfrac{18{.}6}{\sin Y}\\\\ \Rightarrow\ \sin Y &= \dfrac{18{.}6\sin 22^{\circ}}{10}\\
\sin Y &\approx 0{.}6967 \\ \color{red}{\sin^{-1}}\sin Y &\approx \color{red}{\sin^{-1}}0{.}6967 \\ Y &\approx 44{.}2^{\circ}\end{align}||
However, angle Y in the above diagram is an obtuse angle. Therefore, to find the obtuse angle which has a sine value equivalent to the angle of 44.2º, we perform the following operation:
||\begin{align} Y &= 180 - 44{.}2\\ Y &= 135{.}8^{\circ}\end{align}||
The angle Y has a value of 135.8º.
When looking for an angle measurement, always check whether it is an obtuse or acute angle. For an acute angle, the answer is obtained directly. However, for an obtuse angle, subtract the answer obtained from 180 to find the actual value of the angle.
To validate your understanding of trigonometry interactively, consult the following CrashLesson:
