Operations on functions are performed the same way as operations on numbers are performed.
Given two real functions |f| and |g,| the quotient between them is defined as:||\left(\frac{f}{g}\right)(x)= f(x) \div g(x)||
The domain of the quotient function corresponds to the intersection of the domains of the functions in question. If there is a denominator, the restrictions on the latter must be excluded from the final domain.
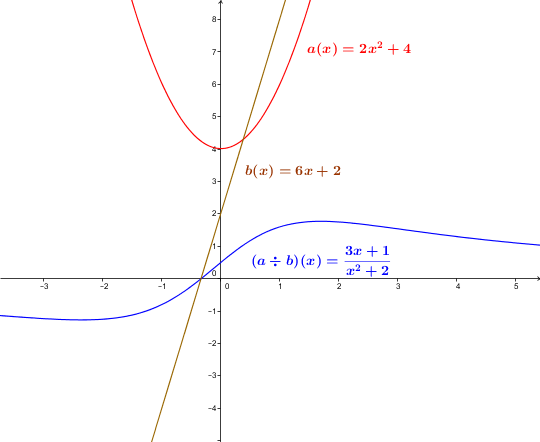
Function |a| is defined by |a(x)=6x+2| and function |b| is defined by |b(x)=2x^{2}+4.| ||\begin{align} \left(\dfrac{a}{b}\right)(x) &= a(x)\div b(x)\quad \text{where}\ b(x)\neq0 \\ &=\dfrac{6x+2}{2x^{2}+4} \\ &=\dfrac{2(3x+1)}{2(x^{2}+2)} \\ &= \dfrac{(3x+1)}{(x^{2}+2)} \end{align}||
The domain of function |a| corresponds to |\mathbb{R}.| The domain of function |b| also corresponds to |\mathbb{R}.| The domain of the function given by |\left(\dfrac{a}{b}\right)| will correspond to the intersection of the two initial domains by removing the values that cancel out the function |b.| However, function |b| is strictly positive, so it never cancels out. Thus, the function’s domain will be |\mathbb{R}.|
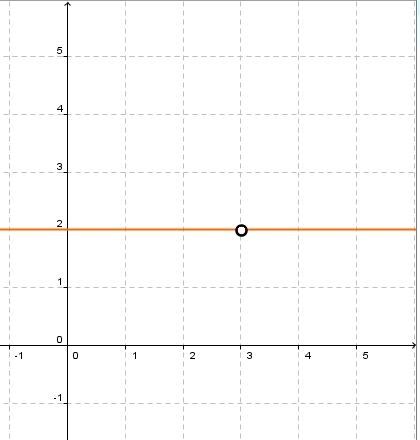
Function |m| is defined by |m(x)=2x-6| and function |n| is defined by |n(x)=x-3.| ||\begin{align} \left(\dfrac{m}{n}\right)(x) &= m(x)\div n(x)\quad \text{where}\ n(x)\neq0 \\ &=\dfrac{2x-6}{x-3} \\ &=\dfrac{2(x-3)}{(x-3)} \\ &= 2 \end{align}||
The domain of function |m| corresponds to |\mathbb{R}|. The domain of function |n| also corresponds to |\mathbb{R}.| The domain of the function given by |\dfrac{m}{n}| will correspond to the intersection of the two initial domains. From this intersection, we need to remove the values that cancel the function |n.| Function |n| becomes zero when |x=3.| Therefore, the domain of the function given by |\dfrac{m}{n}| will be |\mathbb{R} \backslash \lbrace 3 \rbrace.|
The domain of the function given by |\dfrac{m}{n}| will remain |\mathbb{R} \backslash \lbrace 3 \rbrace| after simplification.
To find the quotient of polynomial functions in a graph, divide the range of the first function by the range of the second function.
To produce the graph, create a table of values or use the peculiarities of the resulting function.
Back to Example 1
In the first example, a table of values of the functions |a(x)=6x+2,| |b(x)=2x^{2}+4| and the quotient of the |2| functions results in:
| |x| | |a(x)| | |b(x)| | |a(x)\div b(x)| |
|---|---|---|---|
| |0| | |2| | |4| | |\dfrac{1}{2}| |
| |1| | |8| | |6| | |\dfrac{4}{3}| |
| |2| | |14| | |12| | |\dfrac{7}{6}| |
| |3| | |20| | |22| | |\dfrac{10}{11}| |
| |4| | |26| | |36| | |\dfrac{13}{28}| |
Here is the graphical representation of Example 1:
Here is the graphical representation of Example 2. It is important to remember the restrictions when sketching the quotient of the two functions.
Pour valider ta compréhension des opérations sur les fonctions de façon interactive, consulte la MiniRécup suivante :
