The area of a closed figure is the measurement of its surface.
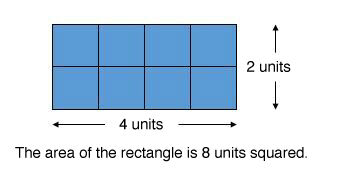
The area is a calculation which makes it possible to physically measure the surface occupied by an object.
The basic unit of measure for area in the International System of Units is the square metre, or |\text{m}^2.|
Here is a table of the most commonly used units to measure area:
|
Prefix |
Kilo- |
Hecto- |
Deca- |
|
Deci- |
Centi- |
Milli- |
|---|---|---|---|---|---|---|---|
|
Area |
Square kilometre (km2) |
Square hectometre (hm2) |
Square decametre (dam2) |
Square metre (m2) |
Square decimetre (dm2) |
Square centimetre (cm2) |
Square millimetre (mm2) |
|
Equivalent value to 1 square metre |
0.000001 |
0.0001 |
0.01 |
1 |
100 |
10000 | 1000000 |
In this table, each unit is 100 times larger than the unit that follows it. Thus, 1 square metre is 100 square decimetres, 1 square decimetre is 100 square centimetres, and so on.
Occasionally, the hectare is used to refer to the area of a piece of land.
1 hectare corresponds to 1 hm2, or 10 000 m2.
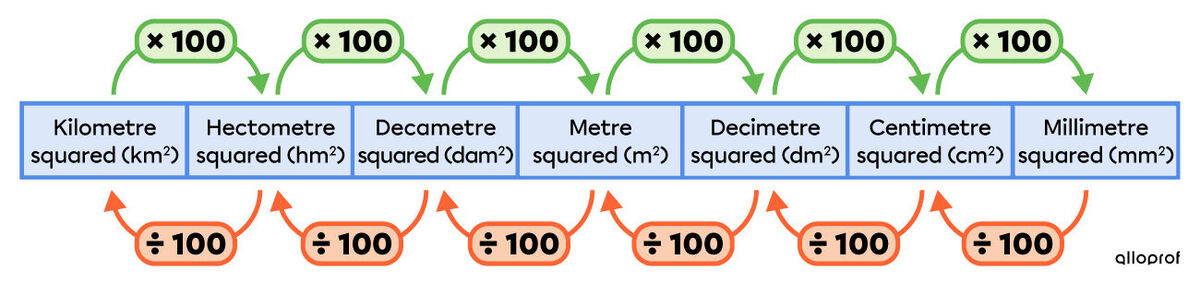
Converting from one unit of measurement to another when measuring area requires multiplying or dividing by 100.
Unlike length measurements, area units differ by a factor of 100.
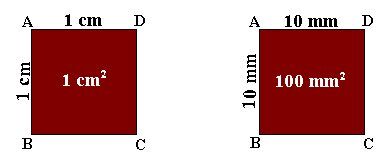
For example, the two following squares have side measurements of 1 cm and 10 mm, respectively. Since 1 cm = 10 mm, both squares are identical, only the measurements are expressed using different units.
-
The area of the first square is 1 cm × 1 cm = 1 cm2
-
The area of the second square is 10 mm × 10 mm = 100 mm2
Therefore, 1 cm = 10 mm, but 1 cm2 = 100 mm2.
The “jump” method or the metric conversion table can be used to convert one unit of measurement to another.
According to this method, it is necessary to:
-
Multiply by 100 for each “jump” (with each unit change) when going from a larger unit to a smaller unit;
-
Divide by 100 for each “jump” (with each unit change) when going from a smaller unit to a larger unit.
We want to convert 2.3 m2 to cm2.
To go from m2 to cm2, multiply by 100 for each “jump” or unit change.

|2{.}3\ \text{m}^2\times100 = 230\ \text{dm}^2|
|230\ \text{dm}^2\times100 = 23\ 000\ \text{cm}^2|
or
|2{.}3\ \text{m}^2\times100\times100 = 2{.}3\ \text{m}^2\times 10\ 000 = 23\ 000\ \text{cm}^2|
Answer: |2{.}3\ \text{m}^2 = 23\ 000\ \text{cm}^2|
According to this method, it is necessary to:
-
Place the ones and tens digit of the number in the position of the given unit of measurement and place the other numbers to the left of it;
-
Put two 0’s in each column, up to the column of the new unit of measurement.
You must always put two digits in each box before changing columns.
We want to convert 34 m2 to cm2.
-
Place the 3 and 4, the tens and the ones digit of the number, in the m2 column.
-
Put two 0's in each column up to the cm2 column.
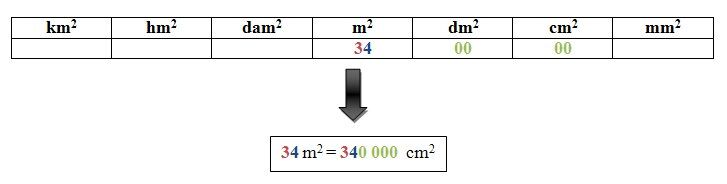
The result is 340 000. There are 340 000 cm2 in 34 m2.
When changing from a smaller unit of measurement to a larger unit, a decimal point must be added in the column of the desired unit of measurement.
We want to convert 7 569 800 m2 into km2.
-
Place the two |0s|, the ones and the tens digit of the number, in the m2 column.
-
The other numbers are placed in pairs moving to the left.

-
Add a decimal point in the km² column.
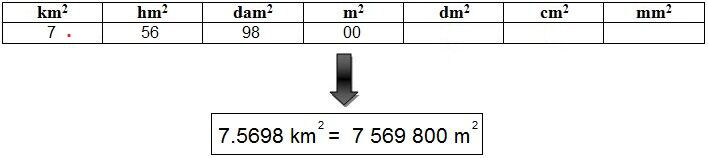
The result is 7.569 800 km2 or 7.5698 km2 , since the |0s| that follow the last digit after the decimal point have no value and are not necessary.