The periscope is an optical instrument that allows sailors to observe the surface of the water, while the submarine is completely underwater.
The periscope operates on a very simple principle. The light rays coming from the light source are reflected by a first plane mirror. They are then reflected again by a second plane mirror so that an image can be seen by the observer.
It is important to remember that plane mirrors invert the image during reflection. The first mirror inverts the image the first time, while the second mirror does the same. As a result, the image is inverted twice, so that it ends up being in the same direction as the original object.
The periscope is a tool for underwater navigation. However, it was also used in the trenches during wartime. Soldiers used a periscope to observe the enemy while remaining hidden in the trenches.
The sextant is an optical device used to measure the angular height of objects in relation to the ground.
The sextant works as follows (the steps correspond to the animated image).
- Point the sextant so as to see the horizon. The observer will perceive two parallel rays (in blue) coming from the horizon. The first ray comes directly from the horizon and the second is reflected twice by plane mirrors before being perceived by the eye. As the two rays are practically overlapping, the observer perceives ‘two horizons’ next to each other.
- Press the clamps to move the index bar that enables the motion of the travelling mirror.
- Move the clamps until the moving mirror aligns the Sun (or star) with the horizon. The ray of light coming from the Sun will become orange, as it is no longer parallel to the horizon ray.
- Release the clamps and use the thumbwheel to adjust the position of the Sun (or star) with the horizon.
- Turn from left to right to ensure perfect alignment between the Sun and the horizon.
- Note the tilt angle measured.
The observer will continue to see the horizon, but will also see the star aligned with the horizon in the fixed mirror. As the body of the sextant is graduated, it will be easy to measure the deflection of the mirror. The angular deviation of the rays on a plane mirror is twice the deflection of the mirror. It will then be possible to conclude from the previous example that if the mirror has rotated by |\small \text {40}^{\circ}|, then the star makes an angle of |\small \text {80}^{\circ}| with the horizon.
The use of a sextant is essential for navigators. Given that the stars have a specific latitude, a sailor who determines the angle at which a star is located can situate himself without difficulty.
A telemeter is an optical device used to measure distances.
The telemeter is composed of three fixed plane mirrors and one movable plane mirror. It is possible for the user to measure the angle of rotation of the movable mirror.
Before taking a measurement with the telemeter, it is important to ensure that the initial rays passing through the two apertures in the telemeter are parallel. It is then that the observer will be able to perceive the object and the horizon juxtaposed in the telemeter.
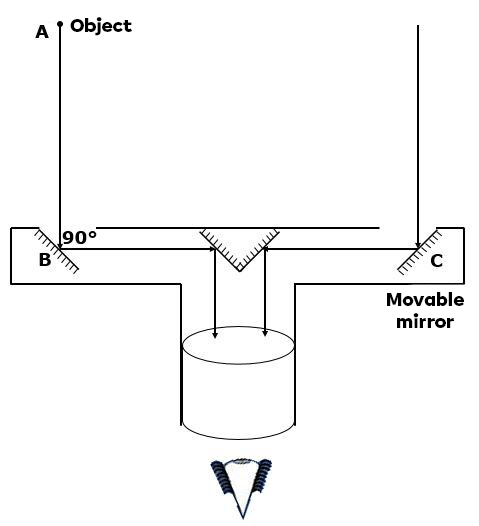
The observer must then turn the movable mirror in order to see the object through the two apertures, as shown in the diagram below.
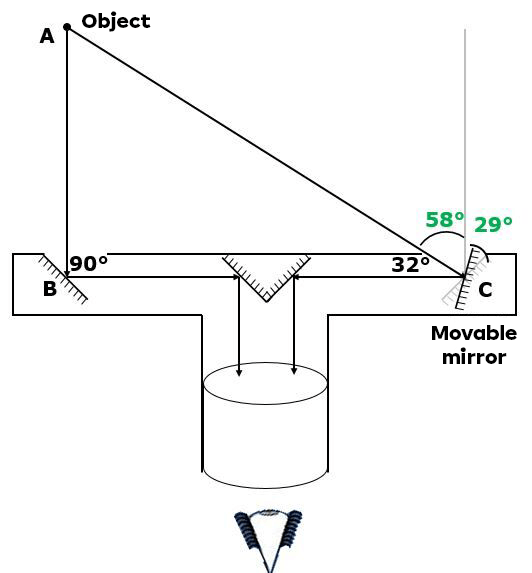
In the situation above, the observer had to rotate the mirror by |\small \text {29}^{\circ}| to see the object. However, a ray reflected by a plane mirror undergoes a deviation equal to twice the rotation of the mirror. We can therefore deduce that the ray on the right side has been deflected by |\small \text {58}^{\circ}| by the rotation of the moving mirror (as indicated by the angles written in green).
From this angle of deflection, it will be possible to calculate angle C of triangle ABC (complementary angles). As the mirror at point B deflects the ray from the |\small \text {90}^{\circ}| (this mirror is set to generate this deflection), it is possible to state that triangle ABC is a right-angled triangle.
Furthermore, it is possible to measure the distance between point B and point C since the mirrors are connected to the telemeter. Given that triangle ABC is a right-angled triangle for which we know the interior angles, it is possible to determine the measurement of segment BC. All we have to do is apply the rules of trigonometry to determine the measurement of segment AB, i.e. the distance separating the object from the observer.
Telemeters are used in topography, the science of producing maps showing landforms and water streams.