The law of reflection states that the angle of incidence is always equal to the angle of reflection. Moreover, the incident ray, the reflected ray, and the normal are located in the same plane.
Une erreur s'est glissée dans cette vidéo.
À 1 min 44 s, la loi de la réflexion, s'applique aussi lors d'une réflexion diffuse. Toutefois, puisque la surface n'est pas lisse, chaque rayon incident à sa propre normale. Les rayons réfléchis ne sont donc pas parallèles entres eux comme dans le cas d'une réflexion spéculaire.
Before analyzing the law of reflection, it is necessary to understand the vocabulary used in light phenomena involving reflection.
| Vocabulary Associated With Reflection on a Polished Surface | |
|---|---|
|
Incident ray |
Ray of light that is directed at a surface. |
|
Reflected ray |
Ray that has been deflected by a surface. |
|
Point of incidence |
Place where the incident ray hits a surface. |
|
Normal |
Line that is perpendicular to a surface at any point |
|
Angle of incidence — |\theta_{i}| |
Angle between the incident ray and the normal. |
|
Angle of reflection — |\theta_{r}| |
Angle between the reflected ray and the normal. |
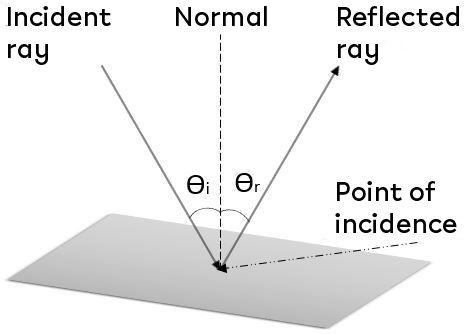
Considering the terms defined above, the law of reflection tells us that if the angle with which a ray of light strikes the surface of a mirror (or a polished surface) relative to the normal is determined, the angle at which this ray will be reflected from the surface of this mirror will be the same.
The law of reflection is defined, in mathematical language, by the following formula.
|\theta_{i} = \theta_{r}|
where
|\theta_{i}| represents the angle of incidence |\small (^{\circ})|
|\theta_{r}| represents the angle of reflection |\small (^{\circ})|
If a ray hits a mirror with an angle of incidence |\theta_{i}| of |\text {40}^{\circ}| relative to normal, it will be reflected with an angle of reflection |\theta_{r}| of |\text {40}^{\circ}.|
It is also important to understand that if several rays arrive with the same angle of incidence, they will all be reflected in the same way.
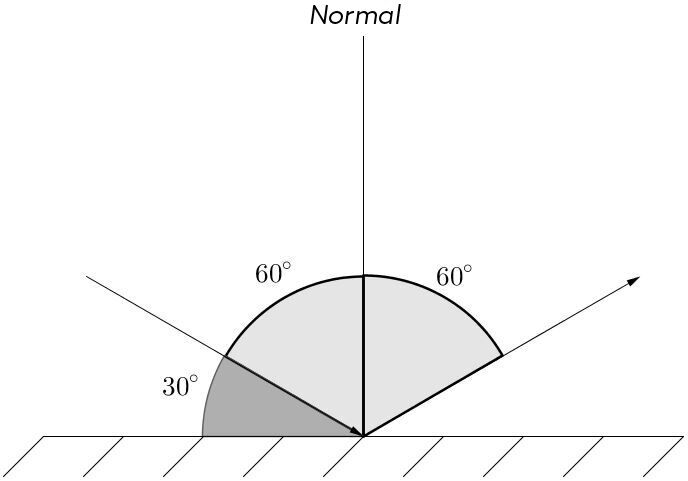
When looking for the angle of reflection of a light ray hitting the surface of a mirror with an angle of |\text {30}^{\circ},| it is important to determine the angle of incidence. Since the normal is a perpendicular line, it forms an angle of |\text {90}^{\circ}| relative to the surface. If the angle between the surface and the light ray is |\text {30}^{\circ},| then the angle between the light ray and the normal, that is the angle of incidence |\theta_{i}|, is therefore |\text {60}^{\circ}.| It is thus possible to determine the angle of reflection |\theta_{r}|, which will also be |\text {60}^{\circ}.|
In the definition of the law of reflection, it is mentioned that the incident ray, the reflected ray, and the normal must be located in the same plane, which is called the plane of incidence. This means that these three elements must be located in the same dimension. In fact, reflection is not possible in a three-dimensional system.
The laws of reflection only apply to specular reflection phenomena.