When a spring or an elastic band is deformed, it reacts by exerting a force to return to its original shape.
The force exerted by the spring or elastic to return to its initial shape is called the restoring force.
Springs are not all made from the same materials and are not all shaped in the same way. They therefore have different properties: two different springs applied with the same force will not deform in the same way.
The spring constant is a characteristic property of springs that determines the force that can be exerted on a spring to cause it to deform over a metre.
The higher the spring constant, the stiffer the spring and the more difficult it is to deform. However, the smaller the constant, the softer the spring and the more likely it is to deform when a force is applied to it.
There is a relationship that determines the restoring force as a function of the deformation that the spring or elastic undergoes.
Hooke's law states that for an ideal spring, the force applied by the spring is equal to the spring's elongation or compression multiplied by the spring's constant.
The mathematical formula for Hooke's law is:
|F_{r} = - k \times \Delta x|
where
|F_{r}| represents the restoring force |\small \text {(N)}|
|k| represents the spring constant |\small \text {(N/m)}|
|\Delta x| represents the elongation or compression of the spring (or elastic) |\small \text {(m)}|. It is calculated by taking the difference between the final position and the initial position |(\Delta x = x_{f} - x_{i})|.
Some editors use the variable |\Delta l| to represent the displacement of the spring. This variable is the same as the |\Delta x| variable used in the formula written above.
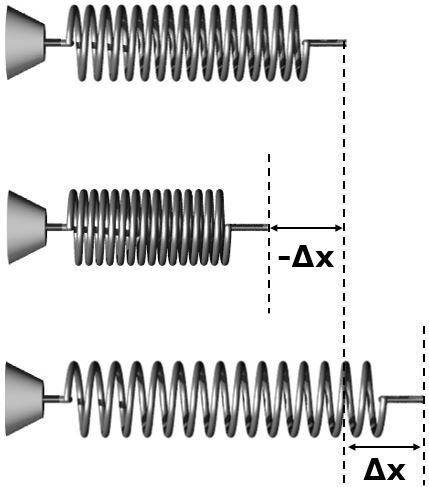
The deformation undergone by a spring can be represented in two ways, either by elongation or compression. As mentioned in the formula, the deformation is represented by the difference between the final position of the spring and its initial position. The following illustration represents these two cases.
If a spring is attached to a wall and stretched to the right, it will also stretch to the right. However, the spring will exert a force to the left to return to its original shape. This force is therefore in the opposite direction to the stretching it is undergoing. This is why there is a negative sign in the formula: it represents the force applied by the spring. If we are looking for the force exerted on the spring, we must ignore the negative sign in Hooke's law.
It is possible to experimentally determine the spring constant of a spring by determining the slope a graph of the restoring force as a function of the deformation of the spring. Simply deform a spring over a predetermined distance and note the force required to produce such a deformation. When the spring stops moving, the forces are balanced: the spring restoring force is equal to the force applied to the spring to deform it.
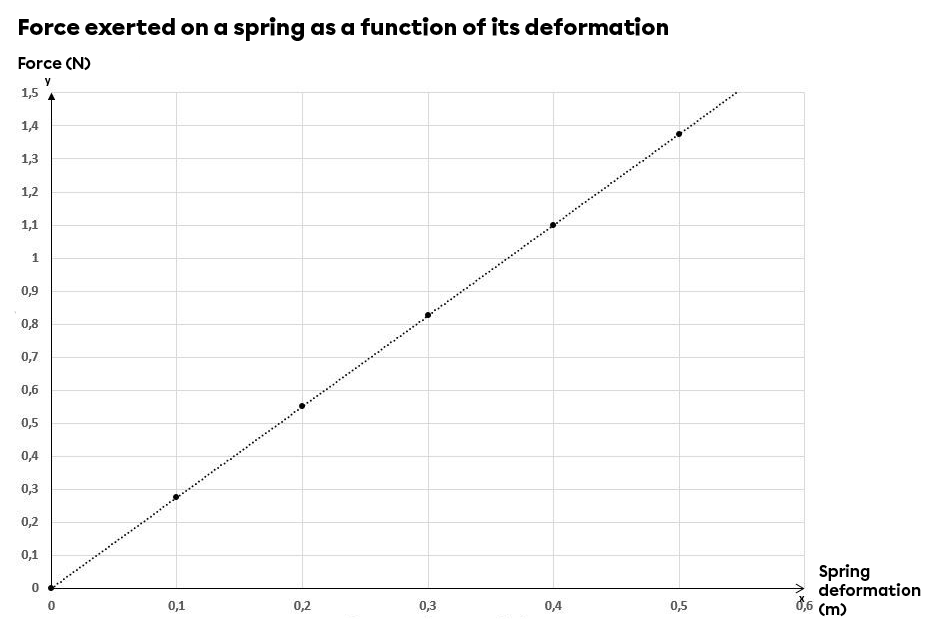
By determining the slope of this graph, the spring constant can be calculated.
||\begin{align}
k = \displaystyle \frac {\Delta y}{\Delta x} \quad \Rightarrow \quad
k &= \displaystyle \frac {(\text {1.1 N - 0 N})}{(\text {0.4 m - 0 m)}} \\
k &= \displaystyle \frac {\text {1.1 N}}{\text {0.4 m}} \\
&= \text {2.75 N/m} \\
\end{align}||
This slope means that if the spring were deformed over one metre, a force of |\small \text {2.75 N}| would be exerted by the spring.
A mass is attached to a spring with a spring constant of |\small \text {15 N/m}|. The spring, which had an initial length of |\small \text {10 cm}|, now has a length of |\small \text {25 cm}|. What will be the final length of the spring if an object with a weight of |\small \text {2.0 N}| is attached to it?
In this case, solving the problem will not take into account the orientation of the forces and the elongation. This is why the negative sign will not be included in Hooke's law equation.
The force initially applied to the spring must first be determined. The known variables are as follows.
||\begin{align} k &= \text {15 N/m} &x_f &= \text {25 cm = 0.25 m} \\ x_{i} &= \text {10 cm = 0.10 m} &\Delta x &= x_f - x_i = \text{0.25 m - 0.10 m = 0.15 m}
\end{align}||
Hooke's law can be used to determine the restoring force.
||\begin{align}
F_{r} = k \times \Delta x \quad \Rightarrow \quad
F_{r} &= \text {15 N/m} \times \text {0.15 m} \\
&= \text {2.25 N}
\end{align}||
The restoring force will be equal to the force applied to the spring if the system is in equilibrium, i.e. the spring is no longer moving.
The final length of the spring must then be determined once the new object is attached. The known variables are as follows.
||\begin{align} k &= \text {15 N/m} &x_f &= \text {?} \\ x_{i} &= \text {10 cm = 0.10 m} &F_{R} &= \text{2.25 N + 2.0 N = 4.25 N}
\end{align}||
Hooke's law can be used to determine the returning force.
||\begin{align}
F_{r} = k \times \Delta x \quad \Rightarrow \quad
\Delta x &= \frac {\text {4.25 N}}{\text {15 N/m}} \\
&= \text {0.28 m}
\end{align}||
To calculate the final position of the spring, we need to use the displacement.
||\begin{align}
\Delta x = x_{f} - x_{i} \quad \Rightarrow \quad
x_{f} &= x_{i} + \Delta x \\
&= {\text {0.10 m + 0.28 m}} \\
&= \text {0.38 m}
\end{align}||
The final length of the spring will therefore be |\text {38 cm}| .
Several springs can be linked together. Springs can be linked in series (1) or in parallel (2), as shown below.
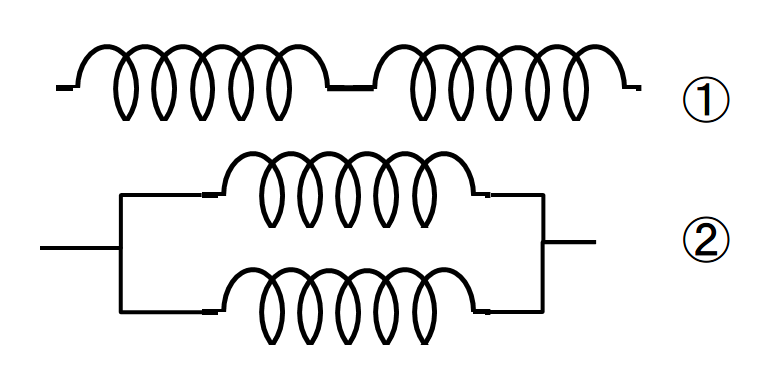
In this case, they can be replaced by a single spring.
(1) Springs in Series
When springs are combined in series, the reciprocal of the equivalent spring rate |k_{eq}| is equal to the sum of the reciprocals of the spring rates specific to each spring.
||\frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2} + \ldots + \frac{1}{k_x}||
(2) Parallel Springs
When springs are combined in parallel, the equivalent spring constant |k_{eq}| is equal to the sum of the spring constants specific to each spring.
||k_{eq} = k_1 + k_2 + \ldots + k_x||