Optical Power |(P)| is the ability of a lens to deviate light rays.
The greater the optical power of a lens, the more the rays are deviated and therefore the closer the focal point is to the optical centre.
Optical power is inversely proportional to focal length.
The following formula can be used to determine the optical power of a lens:
|P = \displaystyle \frac {1}{l_{f}}|
where
|P| represents the optical power of the lens in dioptres |(\delta)|
|l_{f}| represents the focal length in metres |(\text {m})|
Optical power can only be calculated if the focal length is measured in metres.
In addition, by convention, the optical power of a diverging lens is assigned a negative sign.
What is the optical power of a biconcave lens with a focal length of |\text {20 cm}|?
Since the lens is biconcave, the focal length is negative. In addition, the focal length must be transformed into metres.: |l_{f} = -0.20 \: \text {m}.|
||\begin{align} P = \frac {1}{l_{f}} \quad \Rightarrow \quad P &= \frac {1}{-0.20 \: \text {m}} \\ \\ &= -5 \space \delta \end{align}||
The optical power of the biconcave lens is therefore |-5 \: \delta.|
The lens maker's equation (also known as the optrician's equation) is used to calculate the optical power of a lens from its physical characteristics.
First, let's look at how a lens is constructed.
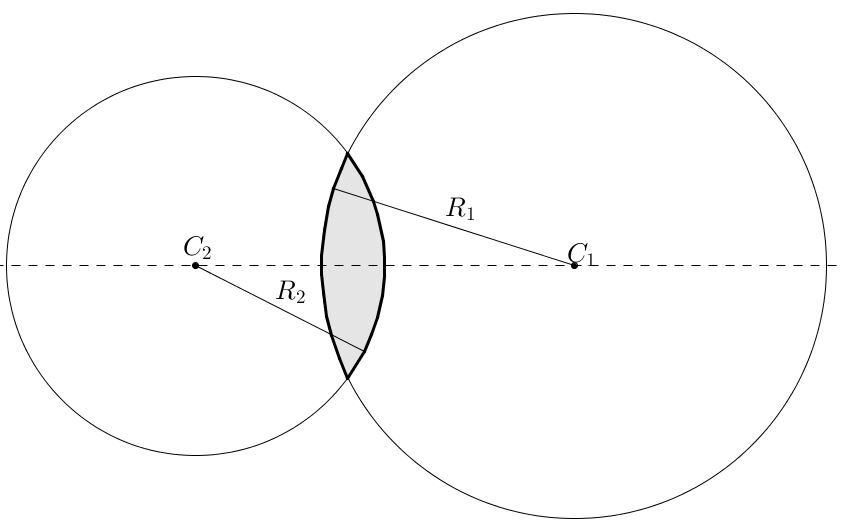
In the diagram above, the lens is coloured grey. The optical power of the lens will depend on the size of the two circles from which the lens originates, and the material used to construct the lens.
The lens maker's equation is defined by the following formula:
|P = (n - 1) \times \displaystyle (\frac {1}{R_{1}} - \frac {1}{R_{2}})|
where
|P| represents the vergence of the lens in dioptres |(\delta)|
|n| represents the refractive index of the lens
|R_{1}| represents the ray of curvature of the first curved surface encountered by the light in metres |(\text{m})|
|R_{2}| represents the radius of curvature of the second curved surface encountered by the light in metres |(\text{m})|
There are a number of important elements to consider in this formula.
- Firstly, the measures of |R_{1}| et |R_{2}| are positive for a convex surface and negative for a concave surface.
- |R_{1}| represents the measure of the radius of the left side of the lens.It does not necessarily represent the circle on the left, as shown in the illustration above. Likewise, |R_{2}| is associated to the measure of the radius of the right side of the lens.
- When one of the side of the lens is flat, like the plano-convex or the plano-concave lens, the radius of curvature is considered infinite. We can therefore remove this ray of curvature from the equation and consider only the ray of curvature of the curved surface.
- Finally, in the brackets |(n-1),| the number 1 represents the index of refraction of air or vacuum. Therefore, if the lens is placed in another environment, it is necessary to modify this by instead inserting the appropriate index of refraction.
| Type of lens | Biconvex | Plano-convex | Converging Meniscus | Biconcave | Plano-concave | Diverging Meniscus |
|---|---|---|---|---|---|---|
| Shape |  |
 |
 |
 |
 |
 |
| |R_{1}| | Positive | Infinite | Negative | Negative | Infinite | Positive |
| |R_{2}| | Negative | Negative | Negative | Positive | Positive | Positive |
In the following illustration, a glass lens|(n = 1.5)| is formed from two circles: the first having a ray of curvature of |R_{1} = \text {35 cm}| and the other having a ray of curvature of |R_{2} = \text {20 cm}.| What is the optical power of this lens?
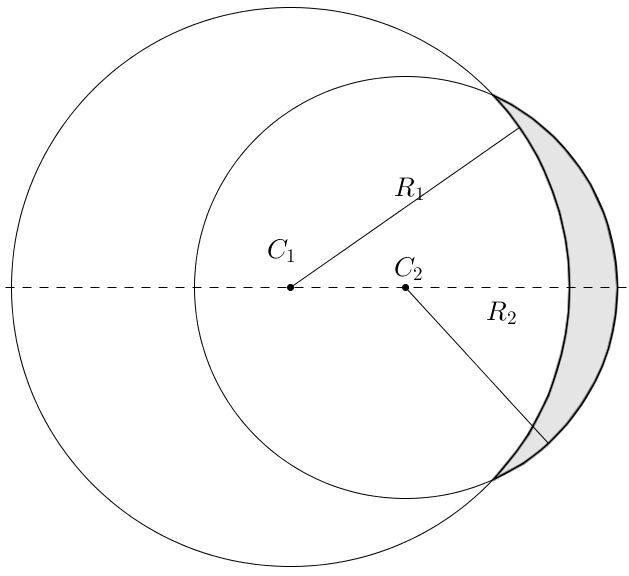
In the illustration above, |R_{1}| et |R_{2}| are associated with concave surfaces. The radii of curvature of both sides will therefore be negative.
The focal lengths must be converted into metres, taking into account the signs.
||\begin{align}R_{1} &= -0.35 \: \text{m} & R_{2} &= - 0.20 \: \text{m} \end{align}||
Using the lens maker's equation :
||\begin{align} P = (n - 1) \times (\frac {1}{R_{1}} - \frac {1}{R_{2}}) \quad \Rightarrow \quad P &=
(1.5 - 1) \times (\frac {1}{- 0.35 \: \text {m}} - \frac {1}{- 0.20 \: \text {m}}) \\ \\
&\cong 1.1 \space \delta \end{align}||
This lens therefore has a positive optical power, which tells us that it is a converging lens.
When several lenses are juxtaposed, the optical power of each lens must be added together (taking into account their respective signs) to determine the optical power of the system.
The optical power of a lens system is calculated using the following formula:
|P_{\text{total}} = P_{1} + P_{2} + P_{3} + ...|
or
|\displaystyle \frac{1}{l_{f_{\text {total}}}}=\frac{1}{l_{f_{1}}}+\frac{1}{l_{f_{2}}}+\frac{1}{l_{f_{3}}}+...|
A diverging lens with a focal length of |10 \: \text{cm}| is placed near a lens with an optical power of |+2.5 \: \delta.| What is the optical power of the system?
To solve this problem, we first need to transform the focal length of the first lens into dioptres. In addition, the sign must be taken into account, since the lens is diverging.
|l_{f} = -0.10 \: \text {m}|
To determine the optical power of this lens:
||\begin{align} P = \displaystyle \frac {1}{l_{f}} \quad \Rightarrow \quad P &= \displaystyle \frac {1}{-0.10 \: \text{m}} \\ \\
&= -10 \: \delta \end{align}||
Simply add the optical power of both lenses to find the optical power of the system of lenses.
||\begin{align} P_{\text{total}} = P_{1} + P_{2} \quad \Rightarrow \quad P_{\text{total}} &=-10 \: \delta + 2.5 \: \delta \\ \\ &= -7.5 \: \delta \end{align}||
The system of lenses is therefore diverging.
A system of three lenses placed side by side is used as the objective lens of a microscope. Lens |L_{1}| has a focal length f |\text {10 cm}| and lens |L_{3}| has a focal length of |\text {50 cm}.| The total optical power of the three-lens system is |5 \: \delta|. What is the optical power of lens |L_{2}|? Is the lens |L_{2}| converging or diverging?
First of all, you must convert all the lengths into metres to use the optical power formula.
||\begin{align}l_{f_{1}} &= 0.10 \: \text{m} &l_{f_{3}} &= 0.50 \: \text{m}\\ \end{align}||
Using the optical power formula:
|P_{2} = ?|
|P_{\text{total}} = 5 \:\delta|
|\begin{align} P_1 = \frac {1}{l_{f}} \quad \Rightarrow \quad P_1 &= \frac {1}{0.10 \: \text{m}} \\ \\ &= 10 \: \delta \end{align}|
|\begin{align} P_3 = \frac {1}{l_{f}} \quad \Rightarrow \quad P_3 &= \frac {1}{0.50 \: \text{m}} \\ \\ &= 2 \: \delta \end{align}|
The optical powers of each lens must be added together to determine the optical power of the system:
||\begin{align} P_{\text{total}} = P_{1} + P_{2} + P_{3} \quad \Rightarrow \quad P_{\text{2}} &= P_{\text{total}} - P_{1} - P_{3} \\\\ &= 5 \: \delta - 10 \: \delta - 2 \: \delta \\\\ &= -7 \: \delta \end{align}||
Since the optical power is negative, the lens is diverging.