To use curved mirror equations, first define variables representing the different measurements that can be taken in the curved mirrors.
| Concave mirror (convergent) | Convex mirror (divergent) |
|---|---|
 |
 |
Variables used in curved mirrors
| Variables | Definition |
| |l_{f}| | Focal length |
| |d_{o}| | Object-lens distance |
| |d_{i}| | Lens-image distance |
| |l_{o}| | Object-focus distance |
| |l_{i}| | Image-focus distance |
| |h_{o}| | Object height |
| |h_{i}| | Image height |
| |R| | Radius of curvature |
Some editors use the variable |p| to represent the object-lens distance and the variable |q| to represent the lens-image distance. These variables are similar to variables defined above: |p| is equivalent to |d_{o}|, while |q| is equivalent to |d_{i}|.
The magnification ( |M| ) of an object is the ratio of the image’s size ( |h_{i}| ) to the size of the object ( |h_{o}| ).
To calculate the magnification, the height ratio can be used. However, it is also possible to use other similar proportions to determine whether the image is larger, smaller or the same size as the object.
To calculate the magnification, use the formula as follows:
|M=\displaystyle \frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}} = \frac {-f}{l_{o}} = \frac {-l_{i}}{f}|
The negative sign present in certain proportions of the above formula is included to respect the sign convention described in this concept sheet.
A magnification value greater than 1 means the image is larger than the object, while a magnification value between 0 and 1 indicates the image is smaller than the object. If the magnification is 1, the height of the image and the object are the same.
The formulas to use in curved mirrors are as follows:
|M=\displaystyle \frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}} = \frac {-f}{l_{o}} = \frac {-l_{i}}{f}|
|\displaystyle \frac {1}{d_{o}} + \frac {1}{d_{i}} = \frac {1}{l_{f}}|
|{d_{i}} = {l_{i}} + {l_{f}}|
|{d_{o}} = {l_{o}} + {l_{f}}|
|{l_{i}} \times {l_{o}} = {l_{f}}^2|
|R = 2 \times {l_{f}}|
The formulas in curved mirrors do not use precise units. All measurements represent length measurements, which can be measured in metres or centimetres. Although the choice of units remains wide, it is important to convert all measurements so they have the same units of measurement.
To make it easier to interpret the data or values in a problem, a sign convention is established. The answers obtained using the formulas described above will be used to determine the characteristics of the image.
Sign convention for mirrors
|
Size |
Positive sign |
Negative sign |
|
Mirror-image distance (|d_{i}|) |
The image is real. | The image is virtual. |
|
Focal length (|l_{f}|) |
The mirror is concave (convergent). | The mirror is convex (divergent). |
|
Magnification (|G|) Image height (|h_{i}|) |
The image is straight. | The image is reversed. |
|
Object-focus distance |(l_{o})| Image-focus distance |(l_{i})| |
Unless the mirror is concave and the object is placed between the vertex and the focus. | Only if the mirror is concave and the object is placed between the vertex and the focus. |
An object |\small \text {5.0 cm}| high is placed |\small \text {25 cm}| in front of a concave (converging) mirror with a focal length of |\small \text {10 cm}| . Where will the image be positioned from the mirror, and how large will it be?
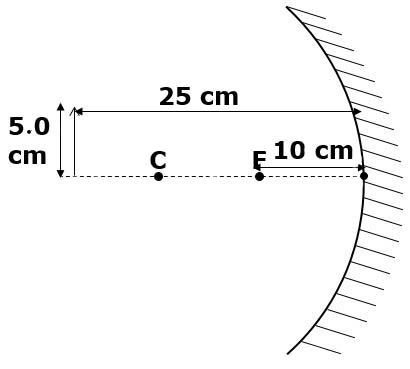
The following is the known information about the problem:
||\begin{align}
h_{o} &= 5.0\:\text{cm} &d_{o} &= 25 \: \text{cm}\\
l_{f} &= 10 \: \text {cm} \\
d_{i} &= \: ? &h_{i} &= \: ? \\
\end{align}||
To find the lens-image distance, the following formula is used:
||\begin{align}
\frac {1}{d_{o}} + \frac {1}{d_{i}} = \frac {1}{l_{f}}
\quad \Rightarrow \quad
\frac {1}{25 \: \text {cm}} + \frac {1}{d_{i}} &= \frac {1}{10\: \text {cm}} \\
0.04 + \frac {1}{d_{i}} &= 0.10 \\
\frac {1}{d_{i}} &= 0.06 \\
{d_{i}} &= 17 \: \text {cm}\\
\end{align}||
The answer obtained has a positive sign: it means the image is real.
To find the height of the image, use the proportions present in the magnification formula.
||\begin{align}
\frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}}
\quad \Rightarrow \quad
{h_{i}} &= \frac {h_{o} \times -d_{i}}{d_{o}} \\
{h_{i}} &= \frac {{5.0 \: \text {cm}} \times -(17 \: \text {cm})}{25 \: \text {cm}} \\
{h_{i}} &= -3.4 \: \text {cm}
\end{align}||
The negative sign indicates that the image is inverted.
The characteristics of the image are as follows: it is real, inverted, smaller than the object (because |h_{i} < h_{o}| ) and between F and C (since the centre of curvature is located at |2 \times f| , that is |20 \text { cm}| ).
We place an object |\small \text {4.2 cm}| high |\small \text {10 cm}| in front of a convex mirror of unknown focal length. The image measures |\small \text {1.4 cm}| height. Determine the focal length of the mirror.
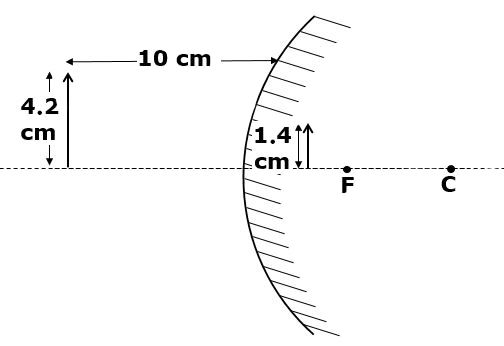
The following is the known information about the problem:
||\begin{align}
h_{o} &= 4.2\:\text{cm} &d_{o} &= 10 \: \text{cm}\\
h_{i} &= +1.4 \: \text {cm} &f &= \: ? \\
\end{align}||
As the mirror is convex, the images are always straight; therefore, the value of the height of the image is necessarily positive.
Since it is not possible to immediately determine the value of |f|, we must first find another value, namely |d_{i}|.
||\begin{align}
\frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}}
\quad \Rightarrow \quad
{d_{i}} &= \frac {-h_{i} \times d_{o}}{h_{o}} \\
{d_{i}} &= \frac {{-1.4 \: \text {cm}} \times 10 \: \text {cm}}{4.2 \: \text {cm}} \\
{d_{i}} &= -3.3 \: \text {cm}
\end{align}||
The negative value was predictable, since diverging mirrors produce virtual images at all times.
Finally, it is possible to determine the focal length using one of the formulas described above.
||\begin{align}
\frac {1}{d_{o}} + \frac {1}{d_{i}} = \frac {1}{l_{f}}
\quad \Rightarrow \quad
\frac {1}{f} &= \frac {1}{10 \: \text {cm}} + \frac {1}{- 3.3 \: \text {cm}} \\
\frac {1}{f} &= 0.1 - 0.3 = \frac {1}{l_{f}} \\
\frac {1}{f} &= -0.2\\
{l_{f}} &= -5 \: \text {cm}
\end{align}||
The focal length of the convex mirror is |\text {5 cm}|. The negative value indicates the mirror is diverging.
What is the object-lens distance in a convex mirror with a focal length of |\small \text {20.0 cm}| if the magnification is |\small \text {0.25}|?
The following is the known information about the problem:
||\begin{align}
f &= -20.0\:\text{cm} &M &= 0.25\\
d_{o} &= \: ? &d_{i} &= \: ? \\
\end{align}||
To find the value of |d_{o}|, the magnification should be used to determine the relationship between |d_{o}| and |d_{i}|.
||\begin{align}
G=\displaystyle \frac {-d_{i}}{d_{o}}
\quad \Rightarrow \quad
0.25 &=\displaystyle \frac {-d_{i}}{d_{o}} \\
-0.25 \times {d_{o}} &= {d_{i}}
\end{align}||
To find the object-lens distance, the following formula is used:
||\begin{align}
\frac {1}{d_{o}} + \frac {1}{d_{i}} = \frac {1}{l_{f}}
\quad \Rightarrow \quad
\frac {1}{d_{o}} - \frac {1}{0.25 \times {d_{o}}} &= \frac {1}{-20.0 \: \text {cm}}\\
\frac {0.25}{0.25 \times d_{o}} - \frac {1}{0.25 \times {d_{o}}} &= \frac {1}{-20.0 \: \text {cm}}\\
\frac {-0,75}{0.25 \times d_{o}}&= \frac {1}{-20.0 \: \text {cm}}\\
{(-0.75)}{(-20.0 \: \text {cm})}&=0.25 \times d_{o} \\
{15 \: \text {cm}}&=0.25 \times d_{o}\\
60 \: \text {cm} &= d_{o}
\end{align}||