A reference system is a coordinate system used to represent elements in space and time.
The following links explain the most important elements of the coordinate systems:
Using a frame of reference is very important in physics, as it enables us to locate an object and determine its state of motion. In addition, a reference system enables us to establish the type of motion observed as a function of the observer's position. The relativity of motion is also dependent on the position of the reference system, since motion can be perceived differently depending on the observer's position.
A soccer player kicks a ball and it follows a parabolic trajectory with a maximum height of 10 m and a range of 50 m. The ball's horizontal and vertical displacement can be graphed if we assume the observer is seated in the stands.
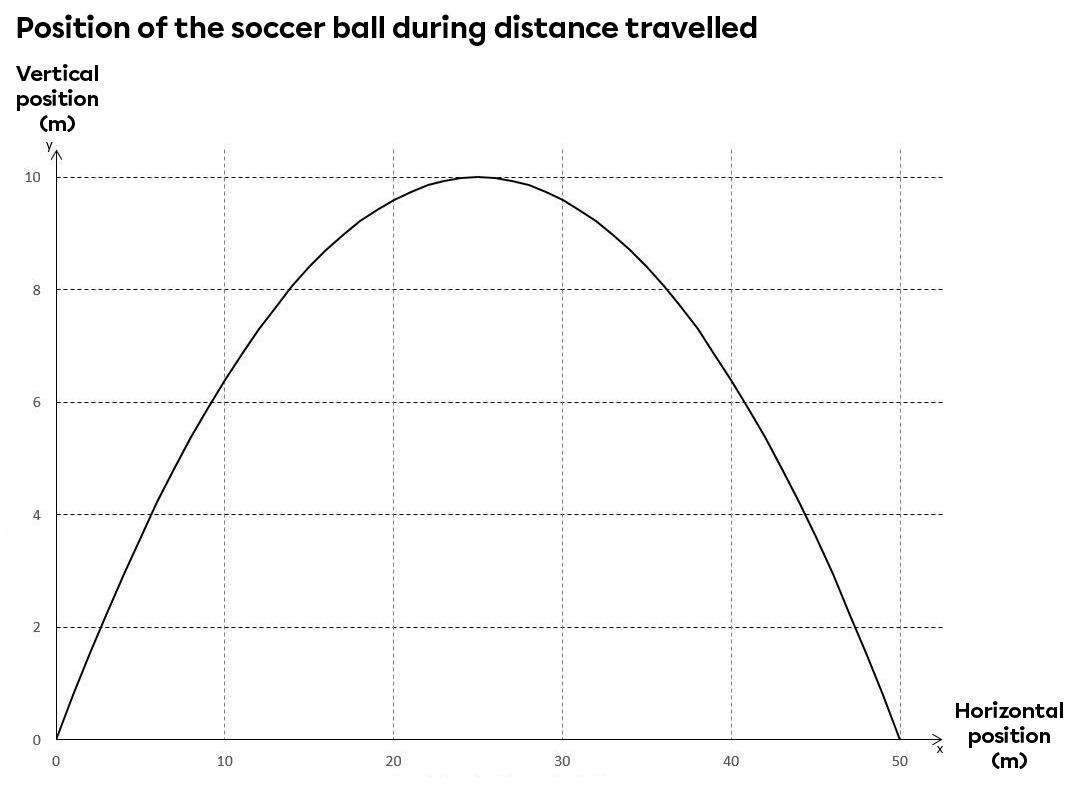
Displacement is not the only variable that can be represented using a reference system. Speed, acceleration and time are other examples of variables that can be plotted on a reference system.
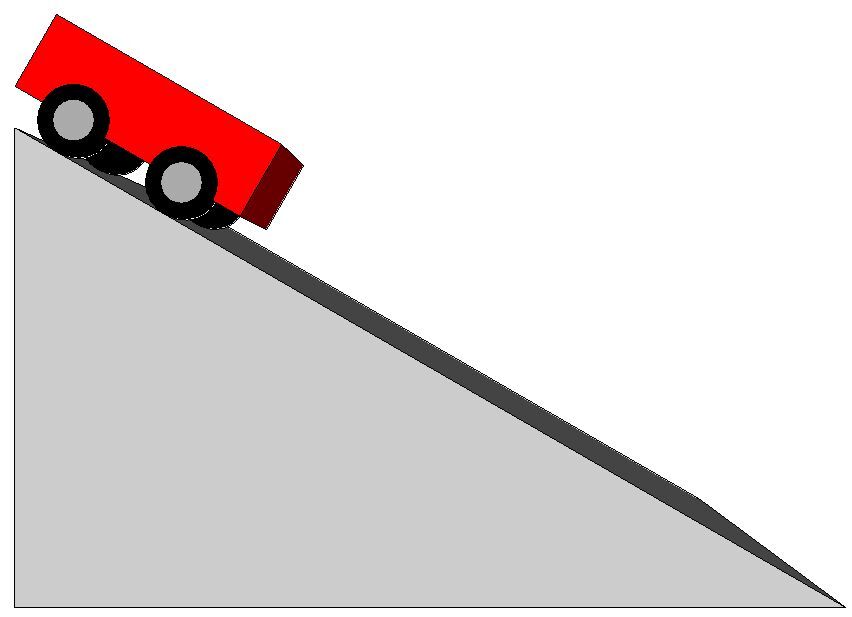
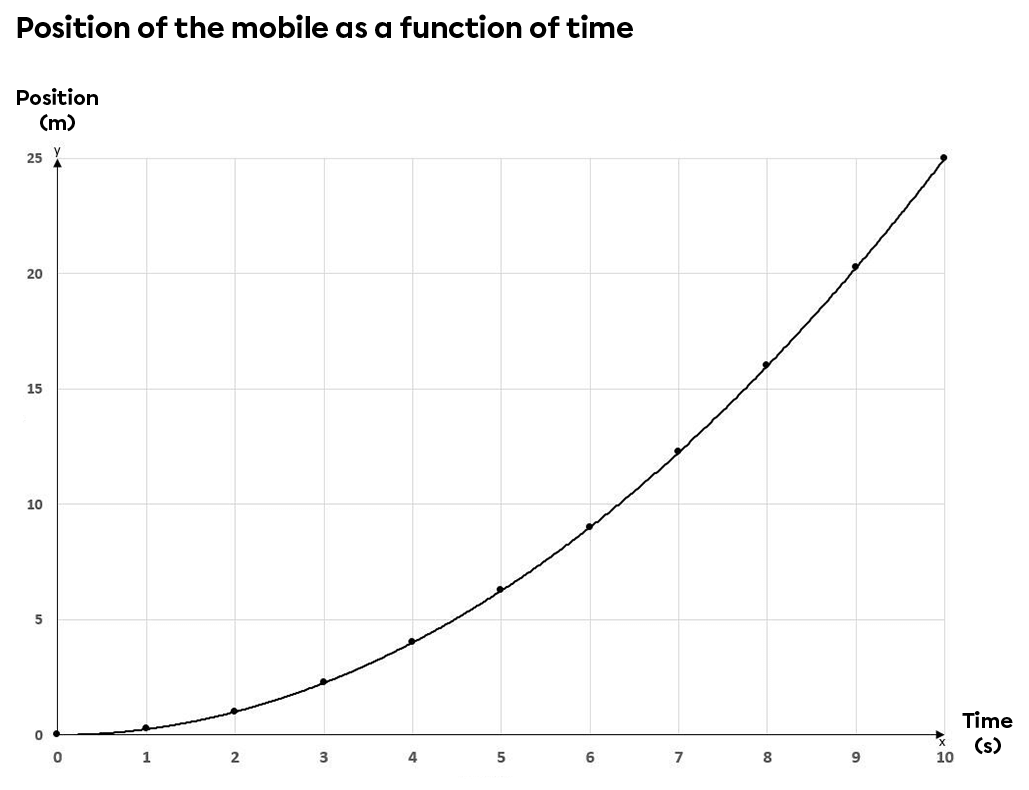
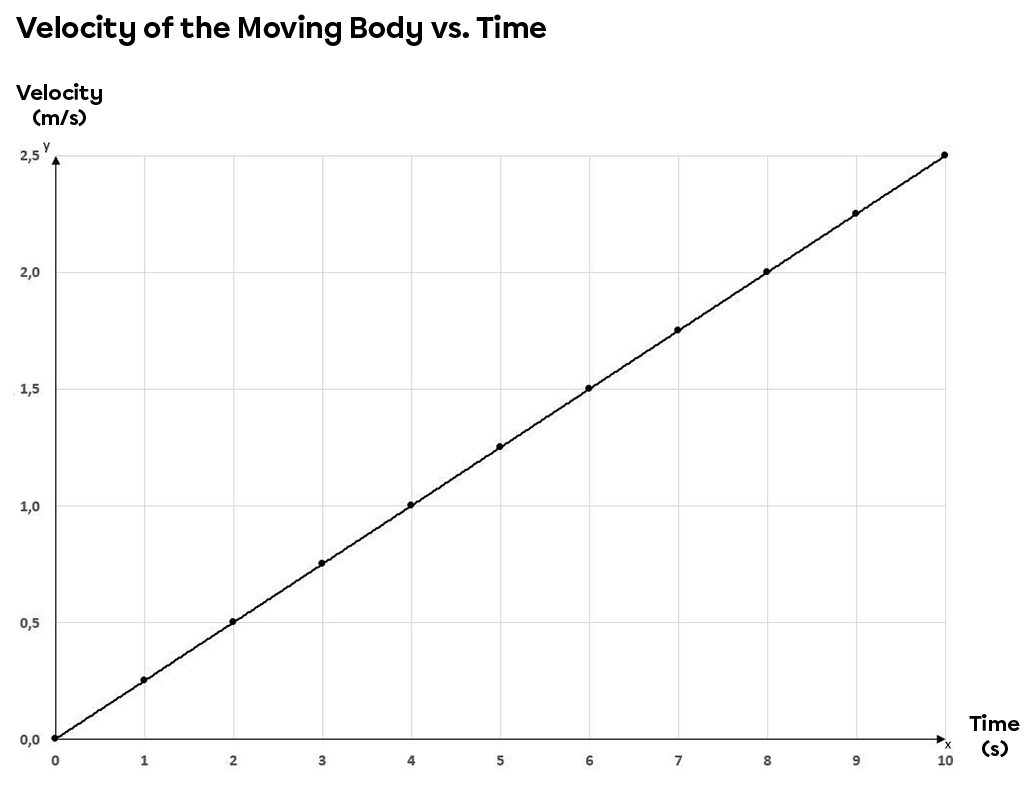
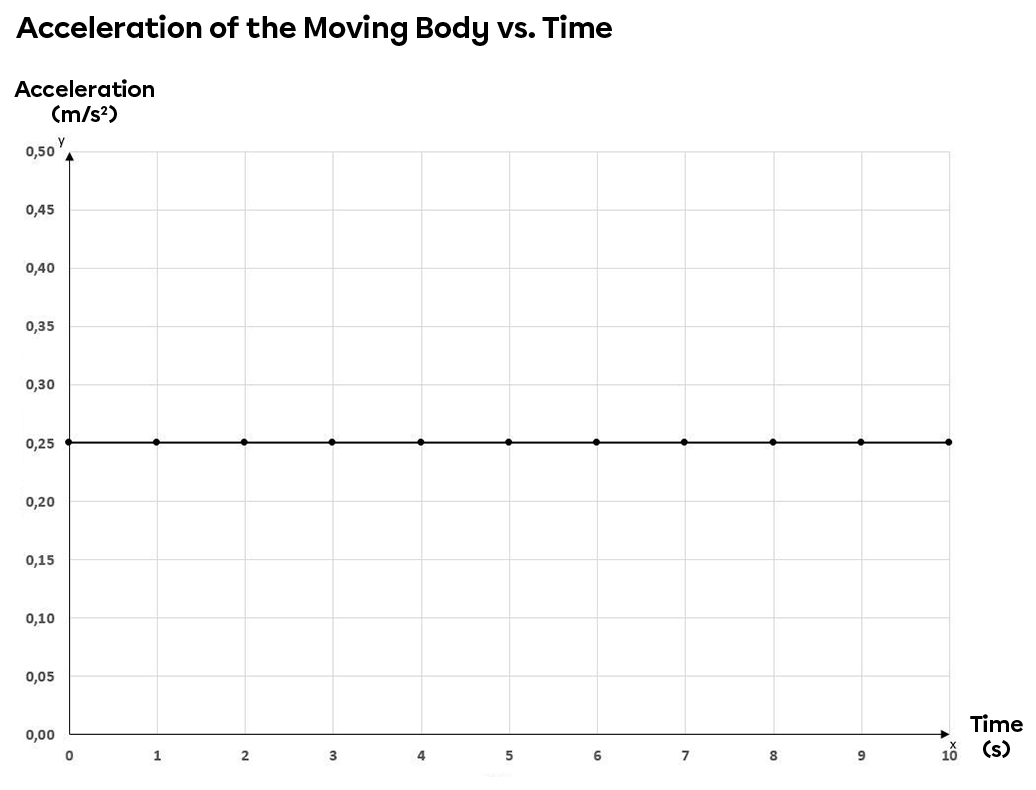
The graphs below show the characteristics (position, speed and acceleration) of a moving object as it moves down an inclined plane in relation to time.
A coordinate system associates a point with precise coordinates that allow it to be situated in space.
There are two types of coordinates:
Cartesian coordinates are |(x,y)|-type coordinates used to locate a point on a Cartesian plane in relation to a point of origin.
To locate an object, three axes may be used:
- the x-axis, or abscissa axis, which corresponds to the horizontal axis;
- the y-axis, or ordinate axis, which corresponds to the vertical axis;
- the z axis, used to position an object according to depth (the third dimension).
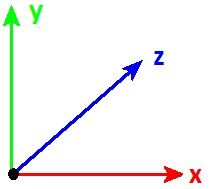
Generally speaking, in most physics problems, only use the first two axes are used.
The Cartesian coordinates of point |\text {A}| shown on the Cartesian plane with origin |\text {O}| are |(2, 3).|

Cartesian coordinates often represent measurable data with units of measurement. It is important to consider the context to know which units of measure should be used to locate a particular point.
Polar coordinates are |(r, \theta)|-type coordinates that enable you to locate a point by using the distance between the starting point and the end point, or the radius r, and the measure of the angle with respect to the positive x-axis, or angle |\theta.|
To find the polar coordinates, first determine the starting point, or the pole. This starting point is similar to the origin of a Cartesian plane. Once this point has been established, determine the value of the radius r by measuring the distance between the starting point and the point we want to locate.
To find the value of angle |\theta|, determine the value of the angle that is located between the positive x-axis, which is our starting point, and the radius determined in the previous step.
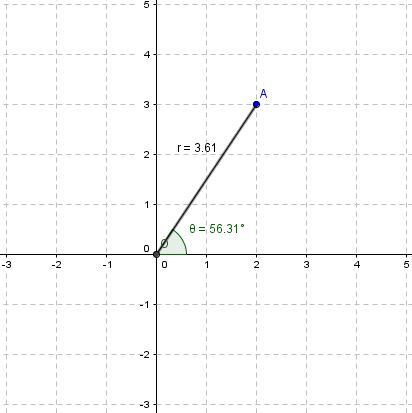
The polar coordinates of point A on the plane below, with pole O, are |(3.61, 56.31^{\circ}).|
Cartesian coordinates can be converted to polar coordinates using the Pythagorean Theorem and the trigonometric ratios in right triangles.
To change from Cartesian coordinates |(x, y)| to polar coordinates |(r, \theta),| apply the following equations:
|| r = \sqrt{x^2 + y^2}|| || \theta= \arctan\left(\frac{y}{x} \right)||
Point B is located at coordinates |(2, 2).| What are the polar coordinates of point B? ||\begin{align}r = \sqrt{x^2 + y^2} \quad \Rightarrow \quad
r &= \sqrt{2^2 + 2^2} \\
&= \sqrt{8} \\
&\approx 2.83 \end{align}||
||\begin{align}\theta=\arctan\left(\frac{y}{x} \right) \quad \Rightarrow \quad
\theta&=\arctan\left(\frac{2}{2} \right) \\
&= \arctan\left(1\right) \\
&= 45^{\circ} \end{align}||
The polar coordinates of point B are therefore |(2.83, 45^{\circ}).|
Polar coordinates can be converted to Cartesian coordinates using the trigonometric ratios.
To change from polar coordinates |(r, \theta)| to Cartesian coordinates |(x, y),| apply the following equations:
||x=r\times \cos \theta|| ||y=r\times \sin \theta||
The polar coordinates of point C are |(3, 30^{\circ}).| What are its Cartesian coordinates?
||\begin{align}x=r\times \cos \theta \quad \Rightarrow \quad
x &= 3\times \cos 30^{\circ} \\
& \approx 2.6 \end{align}||
||\begin{align}y=r\times \sin \theta \quad \Rightarrow \quad
y &= 3\times \sin 30^{\circ} \\
&= 1.5 \end{align}||
The Cartesian coordinates of point C are therefore |(2.6, 1.5).|