Un système de référence est un système de coordonnées dans lequel on peut représenter des éléments dans l'espace et le temps.
Les éléments importants sur le système de coordonnées sont définis dans les liens suivants.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Un système de référence est très important en physique, puisqu’il nous permet de situer un objet et de déterminer l’état de son mouvement. De plus, le système de référence permet d’établir le type de mouvement observé en fonction de la position de l’observateur. La <a href="/fr/eleves/bv/physique/la-relativite-du-mouvement-p1083">relativité du mouvement</a> est d’ailleurs dépendante de la position du système de référence, puisque le mouvement peut être perçu différemment selon la position de l’observateur.</p>
</body></html>
Un joueur botte un ballon de soccer qui suit une trajectoire parabolique dont la hauteur maximale est de |\small \text {10 m}| sur une portée de |\small \text {50 m}|. On peut faire un tracé de son déplacement horizontal et vertical en supposant que l'observateur soit assis dans les estrades.
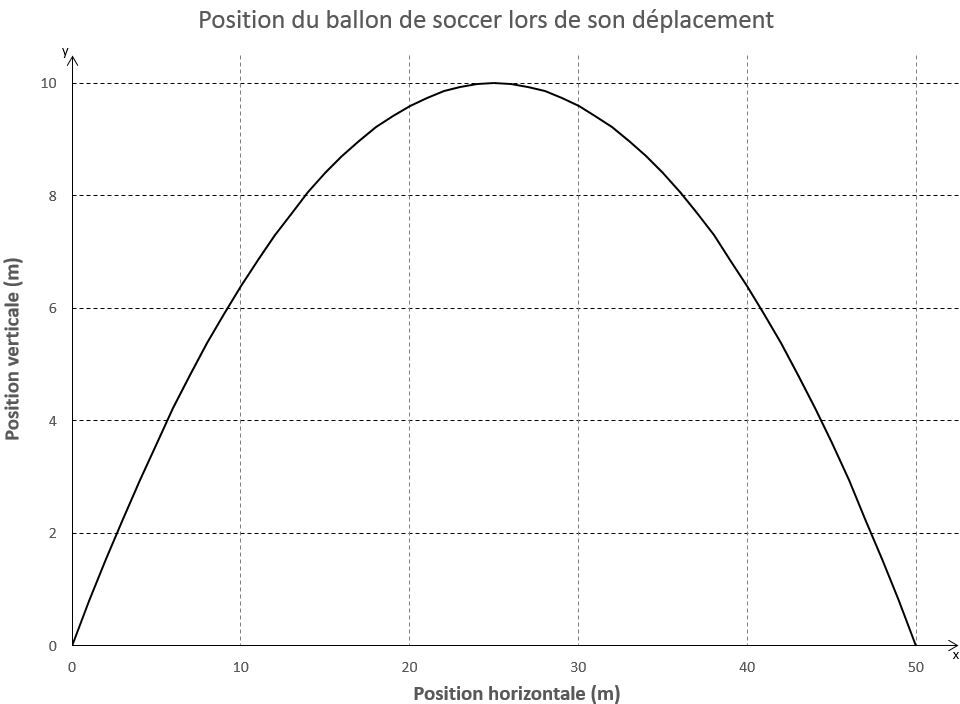
Il n'y a pas que le déplacement que l'on peut tracer dans un système de référence. La vitesse, l'accélération et le temps sont d'autres exemples de variables que l'on peut placer dans un système de référence.
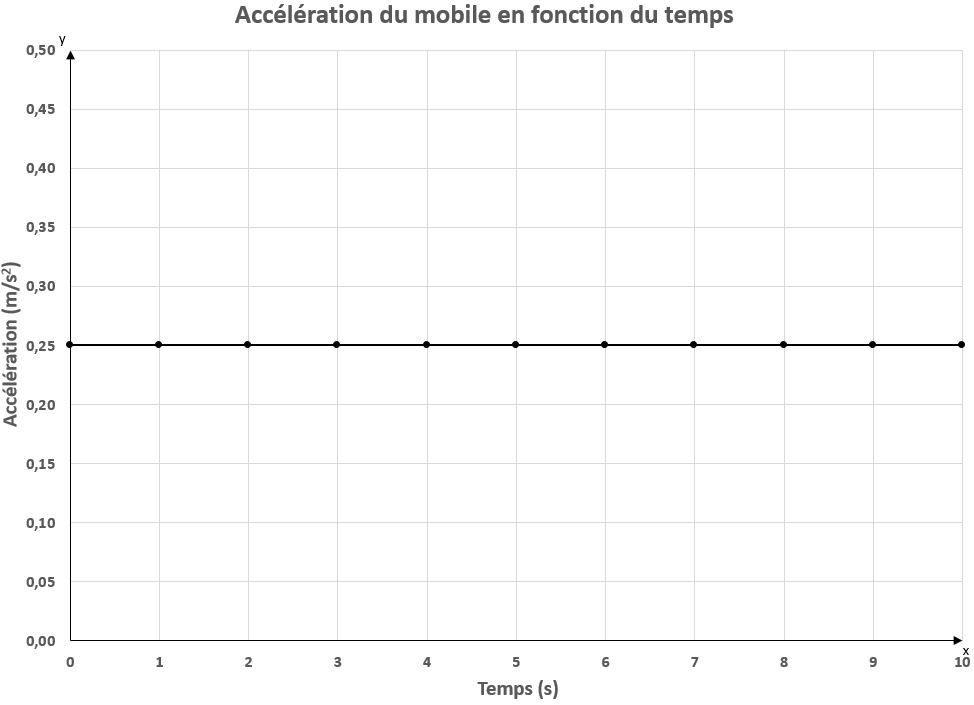
Les graphiques ci-dessous représentent les caractéristiques (position, vitesse et accélération) d'un mobile descendant un plan incliné en fonction du temps.
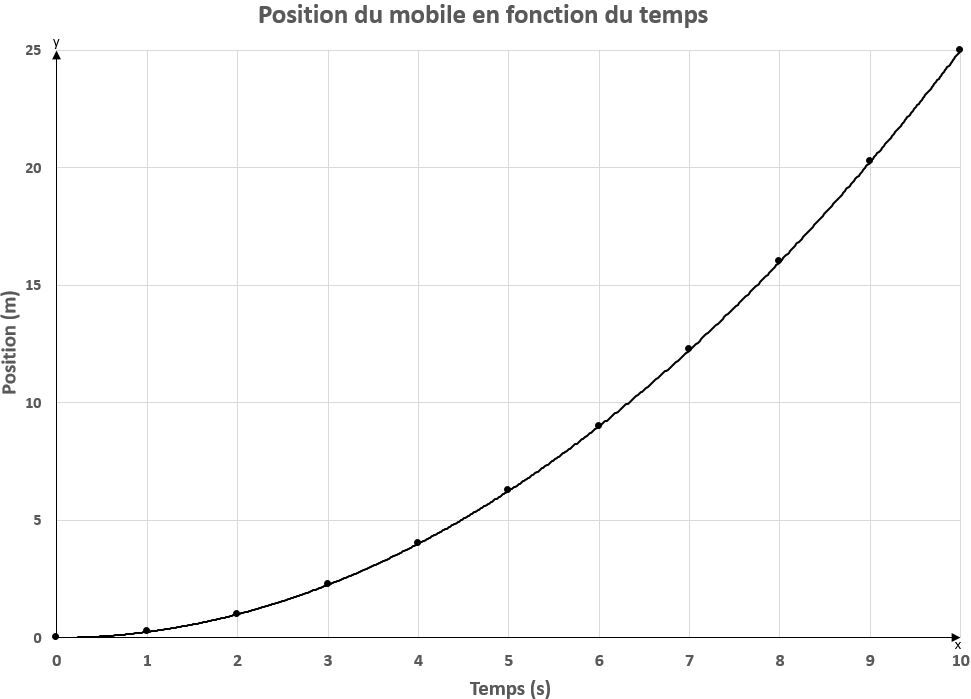
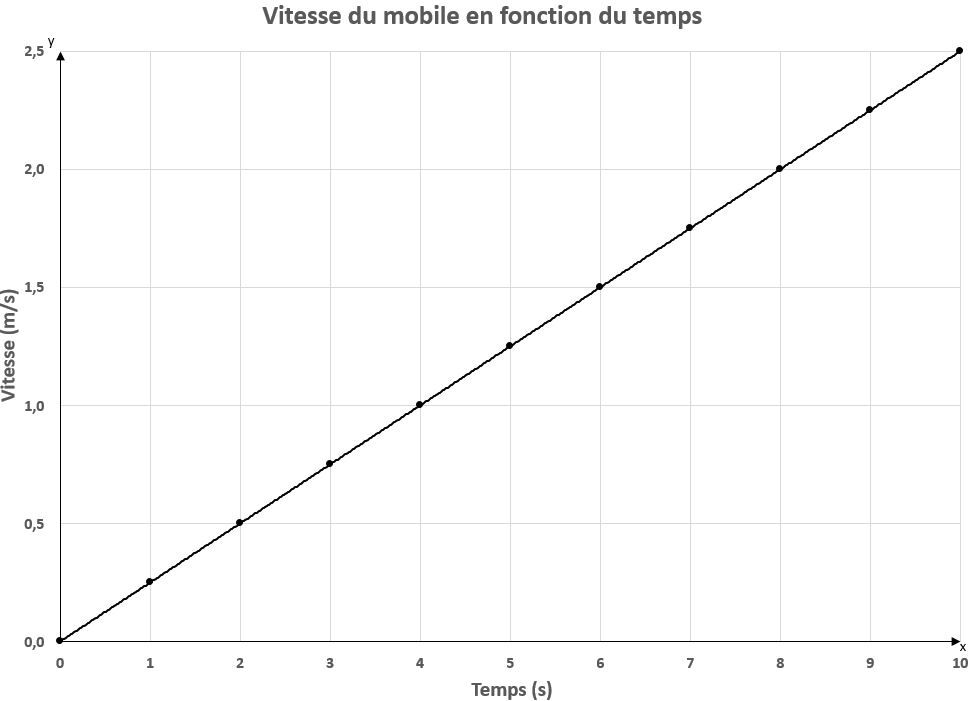
Un système de coordonnées associe un point à des coordonnées précises qui permettent de le situer dans l’espace.
Il existe deux types de coordonnées:
Les coordonnées cartésiennes sont des coordonnées de type |(x, y)| qui permettent de situer un point dans un plan cartésien par rapport à un point d’origine.
Lorsqu’on veut situer un objet, on peut utiliser trois axes :
- l’axe des x, ou axe des abscisses, qui correspond à l’axe horizontal;
- l’axe des y, ou axe des ordonnées, qui correspond à l’axe vertical;
- l’axe des z, qui est utilisé dans la position d’un objet selon la profondeur (la troisième dimension).
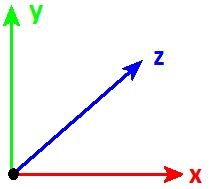
De manière générale, dans les problèmes de physique, nous utiliserons uniquement les deux premiers axes.
Les coordonnées cartésiennes du point |\small \text {A}| illustré dans le plan cartésien d’origine |\small \text {O}| sont |\small (2, 3)|.
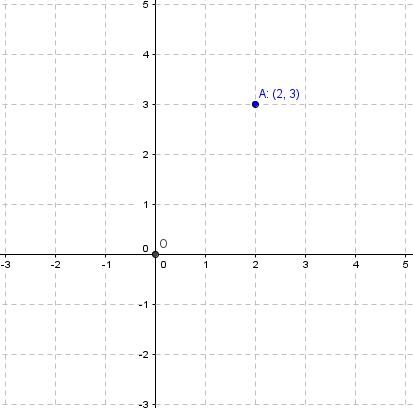
Les coordonnées cartésiennes représentent souvent des données mesurables ayant des unités de mesure. Il est important de tenir compte du contexte afin de savoir quelles unités de mesure doivent être utilisées pour situer un point en particulier.
Les coordonnées polaires sont des coordonnées de type |\small (r, \theta)| qui permettent de situer un point grâce à la distance entre le point de départ et le point final, soit le rayon |\small r|, ainsi que la mesure de l’angle par rapport à l’axe des abscisses positif, soit l'angle |\small \theta|.
Pour déterminer la coordonnée polaire, il faut déterminer le point de départ, soit le pôle. Ce point de départ est un peu comme l’origine d’un plan cartésien. Lorsque ce point a été établi, on détermine la valeur du rayon r en mesurant la distance entre le point de départ et le point que l’on veut situer.
Pour déterminer la valeur de l’angle |\small \theta|, il faut déterminer la valeur de l’angle entre l’axe des abscisses positif, qui est notre point de départ, et le rayon déterminé à l’étape précédente.
Les coordonnées polaires du point A illustré dans le plan ci-dessous dont le pôle est O sont |\small (3,61; 56,31^{\circ})|.
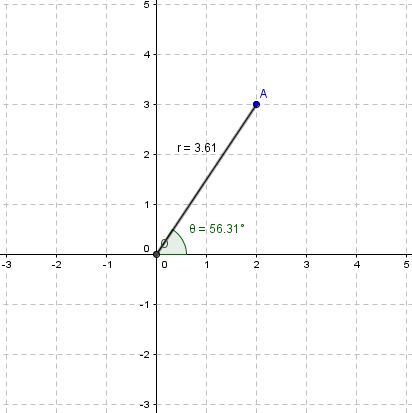
Il est possible de convertir des coordonnées cartésiennes en coordonnées polaires en utilisant le théorème de Pythagore ainsi que les relations trigonométriques.
Pour passer des coordonnées cartésiennes |\small (x, y)| en coordonnées polaires |\small (r, \theta)|, on utilise les règles suivantes:
|| r = \sqrt{x^2 + y^2}|| || \theta=\arctan\left(\frac{y}{x} \right)||
Un point B est situé aux coordonnées |(2, 2)|. Quelles sont les coordonnées polaires du point B?
||\begin{align}r = \sqrt{x^2 + y^2} \quad \Rightarrow \quad
r &= \sqrt{2^2 + 2^2} \\
&= \sqrt{8} \\
&\approx 2,83 \end{align}||
||\begin{align}\theta=\arctan\left(\frac{y}{x} \right) \quad \Rightarrow \quad
\theta&=\arctan\left(\frac{2}{2} \right) \\
&= \arctan\left(1\right) \\
&= 45^{\circ} \end{align}||
Les coordonnées polaires du point B sont donc |(2,83; 45^{\circ})|.
Il est possible de convertir des coordonnées polaires en coordonnées cartésiennes en utilisant les relations trigonométriques.
Pour passer des coordonnées polaires |\small (r, \theta)| en coordonnées cartésiennes |\small (x, y)|, on utilise les règles suivantes:
||x=r\times \cos \theta|| ||y=r\times \sin \theta||
Les coordonnées polaires d’un point C sont |\small (3, 30^{\circ})|. Quelles sont ses coordonnées cartésiennes?
||\begin{align}x=r\times \cos \theta \quad \Rightarrow \quad
x &= 3\times \cos 30^{\circ} \\
& \approx 2,6 \end{align}||
||\begin{align}y=r\times \sin \theta \quad \Rightarrow \quad
y &= 3\times \sin 30^{\circ} \\
&= 1,5 \end{align}||
Les coordonnées cartésiennes du point C sont donc |(2,6; 1,5)|.