La constante d'ionisation de l'eau |K_{(eau)}| est la constante associée à la capacité de l'eau de s'auto-ioniser en ions hydrogène |(H^+)| et en ions hydroxyde |(OH^-)|.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>L’eau pure est une substance qui conduit très faiblement le courant électrique. Une telle <a href="/fr/eleves/bv/sciences/la-conductibilite-electrique-s1021">conductibilité électrique</a> s'explique habituellement par la présence d’ions en solution. En fait, on estime que seules deux molécules d’eau sur un milliard se dissocieraient pour former des ions.</p>
<p>L'eau est une substance amphotère, c'est-à-dire qu'elle est à la fois un acide et une base. En effet, lorsqu'une molécule d'eau se dissocie, elle forme à la fois un ion |H^+|, ce qui correspond à un acide, et un ion |OH^-|, ce qui correspond à une base. L'eau s'auto-ionise au contact d'une seconde molécule d'eau.</p>
</body></html>
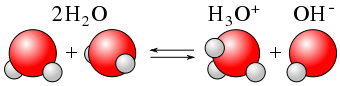
On représente habituellement l'ionisation de la molécule d’eau par l'équation suivante:
|H_{2}O_{(l)} + H_{2}O_{(l)} \rightleftharpoons H_{3}O^{+}_{(aq)} + OH^{-}_{(aq)}|
Cette équation peut être simplifiée de la façon suivante:
|H_{2}O_{(l)} \rightleftharpoons H^{+}_{(aq)} + OH^{-}_{(aq)}|
L'ionisation de l'eau est un processus réversible; il peut donc atteindre l'équilibre. Étant donné que ce système est réversible, on peut utiliser l'expression de la constante d'équilibre de l'eau de la façon suivante:
||K_{H_{2}O}=[H_{(aq)}^{+}]\cdot[OH^{-}_{(aq)}]||
Cette constante d’équilibre de l’eau se nomme aussi constante d'ionisation de l’eau.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Il faut se rappeler que, lors du calcul d’une constante d’équilibre, on ne s’occupe pas de la présence d’un liquide puisque sa concentration ne varie pas. C’est pourquoi la constante d’ionisation de l'eau est une variation de la <a href="/fr/eleves/bv/chimie/la-constante-d-equilibre-c1043">constante d'équilibre</a> obtenue en fonction des concentrations dans laquelle le réactif (l'eau liquide) n'apparait pas.</p>
</body></html>
Lors de la dissociation de l'eau pure, les concentrations en |[H^{+}_{(aq)}]| et en |[OH^{-}_{(aq)}]| sont égales puisqu’il se forme autant d’ions |H^{+}_{(aq)}|que d’ions |OH^{-}_{(aq)}|.
Comme pour toutes les constantes d'équilibre, la valeur de la constante d'ionisation de l'eau varie en fonction de la température. À une température de 25°C, l'eau pure est neutre et son pH est de 7. Ainsi, on peut déduire que la concentration en ions |H^{+}| est de |1\times 10^{-7}|. Conséquemment, la concentration en ions |OH^{-}| est identique. Il est donc possible de déterminer la constante d'ionisation de l'eau de la façon suivante:
|K_{H_{2}O} = [H_{(aq)}^{+}]\cdot[OH_{(aq)}^{-}]|
|K_{H_{2}O} = [1\times 10^{-7}]\cdot[1\times 10^{-7}]|
|K_{H_{2}O} = 1\times 10^{-14}|
Grâce à l'expression de la constante d'ionisation de l'eau, il est possible de calculer la concentration de chacun des ions, qu'il y ait un acide ou une base en solution. En effet, le produit des concentrations de deux ions est toujours constant (|K_{H_{2}O} = 1\times 10^{-14}|) , indépendamment de ce que l'eau contient.
À une température de 25°C, 50 ml d’une solution aqueuse contiennent une concentration en |OH_{(aq)}^{-}| de |5,0\times 10^{-1} M|. On ajoute un volume de 250 ml d’eau. Déterminer la valeur de la concentration finale en |H_{(aq)}^{+}|.
Solution :
On doit au préalable tenir compte du phénomène de dilution, soit :
|V_{i}\times C_{i} = V_{f}\times C_{f}|
|50ml\times [5,0\times 10^{-1}] = 300ml\times [C_{f}]|
|[C_{f}] = [OH_{(aq)}^{-}] = 8,3\times 10^{-2} M|
Alors:
|K_{H_{2}O} = [H_{(aq)}^{+}]\times [OH_{(aq)}^{-}]|
|1\times 10^{-14} = [H_{(aq)}^{+}]\times [8,3\times 10^{-2}]|
|\displaystyle [H_{(aq)}^{+}] = \frac{1\times 10^{-14}}{8,3\times 10^{-2}}|
|[H_{(aq)}^{+}] = 1,2\times 10^{-13} M|