Dans certaines situations, il peut être utile de passer d'une fraction à un nombre fractionnaire ou l'inverse. La fiche suivante propose des méthodes permettant d'effectuer ces passages avec succès.
On peut exprimer en nombre fractionnaire une fraction dont le numérateur est plus grand que le dénominateur.
1. Diviser le numérateur par le dénominateur. Le résultat sera composé d'un entier et d'un reste.
2. Inscrire l'entier suivi d'une fraction dont le numérateur sera le reste et dont le dénominateur sera le même que la fraction d'origine.
Exprime |\displaystyle \frac{14}{5}| sous la forme d'un nombre fractionnaire.
1.Diviser le numérateur par le dénominateur.
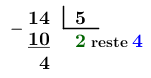
Le résultat est constitué d'un entier (|\color{green}{2}|) et d'un reste (|\color{blue}{4}|).
2. Inscrire l'entier suivi d'une fraction dont le numérateur sera le reste et dont le dénominateur sera le même que la fraction d'origine.

La fraction |\displaystyle \frac{14}{5}| peut donc être exprimée sous la forme du nombre fractionnaire |\displaystyle 2\frac{4}{5}|.
Il est toujours possible d'exprimer un nombre fractionnaire en fraction. Voici deux méthodes permettant d'y arriver.
Cette méthode repose sur le fait que l'on peut exprimer un nombre entier sous la forme d'une fraction dont le dénominateur est |1|.
1. Exprimer la partie entière du nombre fractionnaire sous la forme d'une fraction dont le dénominateur est |1|.
2. Additionner cette fraction et la partie fractionnaire du nombre fractionnaire.
Exprime |\displaystyle 4\frac{2}{3}| en fraction.
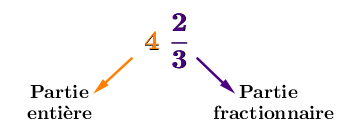
En exprimant la partie entière en fraction, on obtient : |\displaystyle4\Rightarrow \frac{4}{1}|
2. Additionner cette fraction et la partie fractionnaire du nombre fractionnaire.
||\begin{align}\frac{4}{1}+\frac{2}{3}&=\frac{4\color{red}{\times 3}}{1\color{red}{\times 3}}+\frac{2}{3}& &(\text{Mettre sur le même dénominateur})\\
&=\frac{12}{3}+\frac{2}{3}\\
&=\frac{14}{3}\end{align}||
|\displaystyle 4\frac{2}{3}| correspond donc à la fraction |\displaystyle \frac{14}{3}|.
Cette méthode revient plus ou moins aux mêmes manipulations que pour la méthode 1, mais d'une façon plus imagée.
1. Multiplier la partie entière du nombre fractionnaire par le dénominateur de sa partie fractionnaire, puis additionner le numérateur.
2. Écrire le résultat de l'étape 1 au numérateur d'une fraction dont le dénominateur est celui de la partie fractionnaire.
Exprime |8\;\displaystyle \frac{3}{7}| en fraction.
1. Multiplier la partie entière du nombre fractionnaire par le dénominateur de sa partie fractionnaire, puis additionner le numérateur.
Pour cet exemple, la partie entière est |8|, le dénominateur |7| et le numérateur |3|. Ainsi, on obtient: ||8\times 7+3=59||
2. Écrire le résultat de l'étape 1 au numérateur d'une fraction dont le dénominateur est celui de la partie fractionnaire du nombre fractionnaire.
On a obtenu |59| et le dénominateur est |7|. On a donc ||\displaystyle 8\;\displaystyle \frac{3}{7}=\frac{59}{7}||
Cette méthode porte le nom de méthode de la roue, car l'ordre des opérations effectués rappelle un mouvement circulaire.
Reprenons l'exemple ci-haut et analysons les opérations que nous avons effectués.
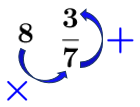
On remarque le mouvement circulaire qui nous a permis d'exprimer le nombre fractionnaire en fraction. ||\displaystyle \frac{8\color{blue}{\times}7\color{blue}{+}3}{7}=\frac{59}{7}|| C'est un bon truc pour retenir cette méthode!