Pour dessiner un cercle, on doit utiliser un outil : le compas. Un compas possède deux pointes : une pointe sèche et une pointe à mine. La pointe sèche est composée d’une aiguille qui pointe le centre du cercle alors que la pointe à mine est composée d’un crayon ou d’une mine qui permet de tracer le cercle ou des arcs de cercle.

Pour en savoir plus sur le cercle, il est possible de consulter le lien suivant :
Par définition, un cercle est défini selon deux aspects: son centre et son rayon. Ainsi, ce sont les deux seules informations que l'on doit posséder pour tracer cette figure géométrique.
Voici les étapes permettant de dessiner un cercle.
-
Ouvrir le compas selon la mesure du rayon (distance entre le centre et le point donné) du cercle à tracer.
-
Déposer la pointe sèche sur le centre du cercle à tracer sur la feuille.
-
Pivoter le compas autour de la pointe sèche pour que la pointe à mine se déplace sur le papier de façon circulaire donnant, une fois un tour complété, un cercle.
Concrètement, on peut représenter le tout de la façon suivante.
|
1. Ouvrir le compas selon la mesure du rayon du cercle à tracer.
|
2. Déposer la pointe sèche sur le centre du cercle à tracer sur la feuille.
|
3. Pivoter le compas autour de la pointe sèche pour que la pointe à mine se déplace sur le papier de façon circulaire donnant, une fois un tour complété, un cercle.
|
Pour y arriver, on doit se servir de certaines propriétés du cercle. Plus précisément, on utilisera le fait que les médiatrices des cordes d'un cercle se croisent précisément au centre de celui-ci.
-
À l'aide de la règle, relier les trois points avec 2 segments distincts afin de former 2 cordes du cercle.
-
Tracer la médiatrice de chacune des cordes.
-
Placer la pointe sèche du compas sur le point d'intersection des médiatrices et placer la pointe à mine du compas sur un des trois points.
-
Tracer le cercle.
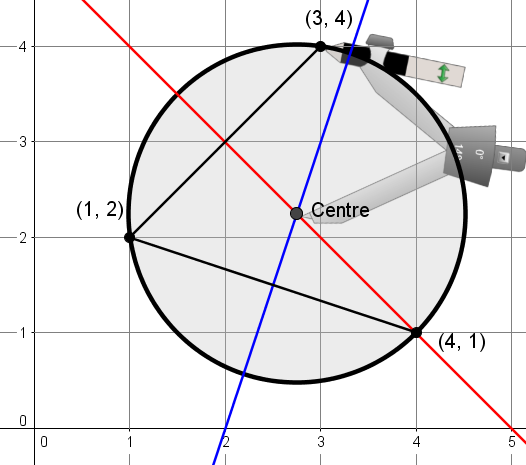
En suivant ces étapes de construction, on s'assure de trouver le seul et unique cercle qui passe par les trois points donnés.
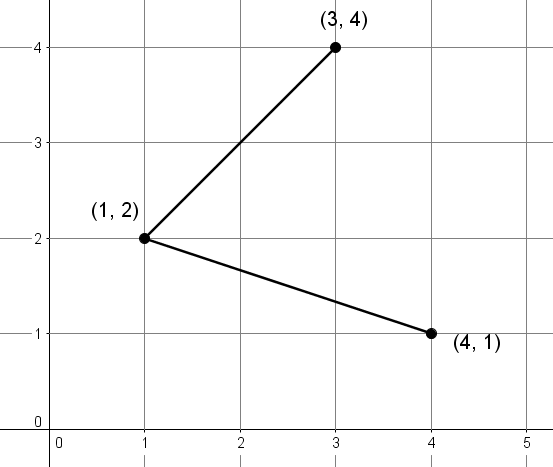
Trace un cercle qui passe par les points |\left(1,2\right),| |\left(3,4\right)| et |\left(4,1\right).|
|
1. Relier les 3 points avec 2 segments distincts afin de former les 2 cordes du cercle.
|
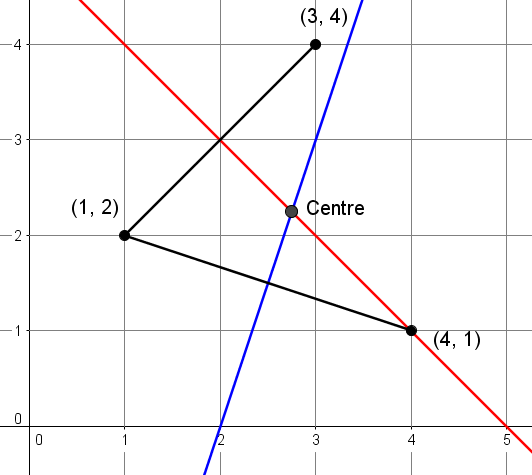
2. Tracer la médiatrice de chacune des cordes.
|
|
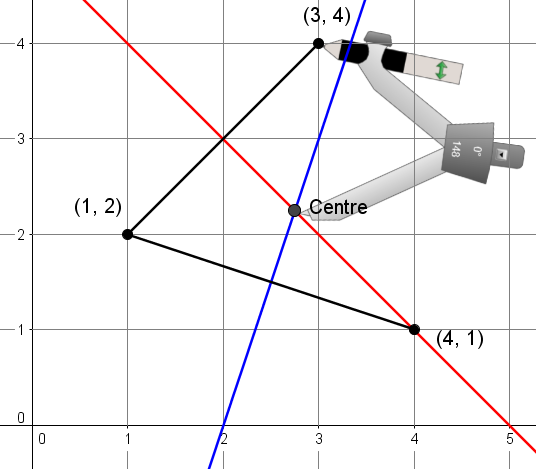
3. Placer la pointe sèche du compas sur le point d'intersection des médiatrices et placer la pointe à mine du compas sur un des 3 points.
|
4. Tracer le cercle.
|
En géométrie, un cercle inscrit à un polygone est un cercle qui est tangent à tous les côtés de ce polygone.
La méthode suivante permet de construire un cercle inscrit à un triangle |ABC|. Afin de tracer un cercle inscrit à un polygone régulier, il suffit de tracer les bissectrices de chacun des angles et de suivre les étapes 4 et 5 décrites ci-dessous.
-
Construire la bissectrice de l'angle A.
-
Construire la bissectrice de l'angle B.
-
Construire la bissectrice de l'angle C.
-
Identifier un rayon qui est perpendiculaire à l'un des côtés du triangle.
-
Utiliser ce rayon afin de tracer le cercle à l'aide du compas.
Pour être en mesure de tracer ce type de cercle, il faut être à l'aire avec la construction d'une médiatrice et d'une bissectrice avec un compas.
Trace un cercle inscrit dans le triangle ABC suivant.
|
1. Construire la bissectrice de l'angle A.
|
2. Construire la bissectrice de l'angle B.
|
|
3. Construire la bissectrice de l'angle C.
|
4. Identifier un rayon qui est perpendiculaire à l'un des côtés du triangle.
|
|
5. Utiliser ce rayon afin de tracer le cercle à l'aide du compas.
|
|
En géométrie, un cercle circonscrit à un polygone est un cercle qui passe par tous les sommets de ce polygone.
La méthode suivante permet de contruire un cercle circonscrit à un triangle |\small ABC|. Afin de tracer un cercle circonscrit à un polygone régulier, il suffit de tracer les médiatrices de chacun des côtés et de suivre les étapes 4 et 5 décrites ci-dessous.
-
Construire la médiatrice du segment AB.
-
Construire la médiatrice du segment AC.
-
Construire la médiatrice du segment BC.
-
Placer la pointe sèche du compas sur le centre du cercle (point d'intersection des trois médiatrices) et la pointe à mine sur un des sommets du polygone pour finalement tracer le cercle.
Pour y arriver, on doit être en mesure de construire une médiatrice avec un compas.
|
1. Construire la médiatrice du segment AB.
|
2. Construire la médiatrice du segment AC.
|
|
3. Construire la médiatrice du segment BC.
|
4. Placer la pointe sèche du compas sur le centre du cercle (point d'intersection des trois médiatrices) et la pointe à mine sur un des sommets du polygone pour finalement tracer le cercle.
|