Il n'existe pas de procédure qui permette à tout coup de démontrer des énoncés à l'aide des vecteurs.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Cependant, certaines stratégies peuvent s'avérer efficaces et permettre la démonstration de tels énoncés.</p>
<ol>
<li>Monter un plan de démonstration (dans sa tête ou par écrit) avant de se lancer dans les calculs.</li>
<li>Travailler de façon structurée. Des tableaux comme ceux utilisés dans les exemples présentés plus bas permettent souvent d'effectuer une démonstration plus claire.</li>
<li>Mettre à profit la relation de Chasles.</li>
<li>Utiliser les <a href="/fr/eleves/bv/mathematiques/les-proprietes-des-operations-sur-les-vecteurs-m1302">propriétés des vecteurs et des opérations vectorielles</a>.</li>
</ol>
</body></html>
| Affirmations | Justifications |
| |\mid \mid \overrightarrow{u}\mid \mid =\sqrt{a^{2}+b^{2}}| | Par définition |
| |-\overrightarrow{u}=(-a,-b)| | Vecteur opposé |
| |\mid \mid - \overrightarrow{u}\mid \mid =\sqrt{(-a)^{2}+(-b)^{2}}| | Par définition |
| |\mid \mid -\overrightarrow{u}\mid \mid =\sqrt{a^{2}+b^{2}}| | Par calculs |
| Les côtés droits des affirmations 1 et 4 sont identiques. | Constatation |
| |\mid \mid \overrightarrow{u}\mid \mid =\mid \mid -\overrightarrow{u}\mid \mid | | Par transitivité |
Posons que |\overrightarrow{u}=(r,s)|.
| Affirmations | Justifications |
| |\overrightarrow{u} \cdot \overrightarrow{u}=ac+bd| | Définition du produit scalaire |
| |\overrightarrow{u} \cdot \overrightarrow{u} =r^{2}+s^{2}| | Avec les bonnes composantes |
| |\mid \mid \overrightarrow{u}\mid \mid ^{2}=(\sqrt{a^{2}+b^{2}})^{2}| | Par définition |
| |\mid \mid \overrightarrow{u}\mid \mid ^{2}=(\sqrt{r^{2}+s^{2}})^{2}| | Avec les bonnes composantes |
| |\mid \mid \overrightarrow{u}\mid \mid ^{2}=r^{2}+s^{2}| | Par calculs |
| Les côtés droits des affirmations 3 et 6 sont identiques. | Par constatation |
| |\overrightarrow{u} \cdot \overrightarrow{u}=\mid \mid \overrightarrow{u}\mid \mid ^{2}| | Par transitivité |
Hypothèse : |ABCD| est un losange.
Conclusion : |\overrightarrow{AC}\perp\overrightarrow{BD}|
Il faut donc démontrer que |\overrightarrow{AC}\cdot\overrightarrow{BD}=0| (produit scalaire).
| Affirmations | Justifications |
| |\overrightarrow{AC}\cdot\overrightarrow{BD}=(\overrightarrow{AB}+\overrightarrow{BC})\cdot(\overrightarrow{BA}+\overrightarrow{AD})| | Par la relation de Chasles |
| |\overrightarrow{AC}\cdot\overrightarrow{BD}=(\overrightarrow{AB}+\overrightarrow{AD})\cdot(\overrightarrow{BA}+\overrightarrow{AD})| | Ce sont les côtés congrus d'un losange |
| |\overrightarrow{AC}\cdot\overrightarrow{BD}=(\overrightarrow{AD}+\overrightarrow{AB})\cdot(\overrightarrow{AD}+\overrightarrow{BA})| | Par commutativité |
| |\overrightarrow{AC}\cdot\overrightarrow{BD}=(\overrightarrow{AD}+\overrightarrow{AB})\cdot(\overrightarrow{AD}-\overrightarrow{AB})| | Vecteur opposé |
| |\overrightarrow{AC}\cdot\overrightarrow{BD}=\overrightarrow{AD}^2-\overrightarrow{AB}^2| | Différences de carrés |
| |\overrightarrow{AC}\cdot\overrightarrow{BD}=\mid \mid \overrightarrow{AD}\mid \mid ^{2}-\mid \mid \overrightarrow{AB}\mid \mid ^{2}| | |\overrightarrow{u}^{2}=\mid \mid \overrightarrow{u}\mid \mid ^{2}| |
| |\overrightarrow{AC}\cdot\overrightarrow{BD}=\mid \mid \overrightarrow{AB}\mid \mid ^{2}-\mid \mid \overrightarrow{AB}\mid \mid ^{2}| | Côtés congrus d'un losange |
| |\overrightarrow{AC}\cdot\overrightarrow{BD}=0| | Par soustraction |
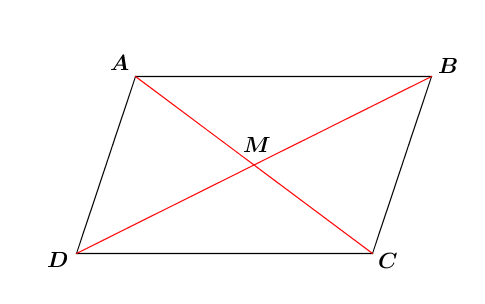
Hypothèses : |ABCD| est un parallélogramme et |M| est le point milieu de la diagonale |AC|.
Conclusion : |M| est le point milieu de la diagonale |DB|. Ainsi, il faut démontrer que |\overrightarrow{MB}=\overrightarrow{DM}|.
| Affirmations | Justifications |
| |\overrightarrow{DM}=\overrightarrow{DA}+\overrightarrow{AM}| | Relation de Chasles |
| |\overrightarrow{DM}=\overrightarrow{CB}+\overrightarrow{AM}| | Côtés opposés d'un parallélogramme |
| |\overrightarrow{DM}=\overrightarrow{CB}+\overrightarrow{MC}| | Par hypothèse |
| |\overrightarrow{DM}=\overrightarrow{MC}+\overrightarrow{CB}| | Commutativité de l'addition |
| |\overrightarrow{DM}=\overrightarrow{MB}| | Relation de Chasles |

Hypothèses : |ABC| est un triangle et |\overrightarrow{AM}=\overrightarrow{MB}| puis |\overrightarrow{BN}=\overrightarrow{NC}|.
Conclusion : |\displaystyle \overrightarrow{MN}=\frac{1}{2} \overrightarrow{AC}|
| Affirmations | Justifications |
| |\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}| | Relation de Chasles |
| |\overrightarrow{AC}=(\overrightarrow{AM}+\overrightarrow{MB})+(\overrightarrow{BN}+\overrightarrow{NC})| | Relation de Chasles |
| |\overrightarrow{AC}=\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{BN}+\overrightarrow{BN}| | Par hypothèse |
| |\overrightarrow{AC}=2\overrightarrow{MB}+2\overrightarrow{BN}| | Addition de vecteurs |
| |\overrightarrow{AC}=2(\overrightarrow{MB}+\overrightarrow{BN})| | Mise en évidence |
| |\overrightarrow{AC}=2\overrightarrow{MN}| | Relation de Chasles |
| |\displaystyle \frac{1}{2} \overrightarrow{AC} = \overrightarrow{MN}| | Division par 2 |
Pour valider ta compréhension à propos des démonstrations de façon interactive, consulte la MiniRécup suivante :

Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
