Pour soustraire un polynôme à un autre, il faut additionner l'opposé de chacun des termes semblables du second polynôme à ceux du premier et réduire l'expression algébrique obtenue. On obtient alors un nouveau polynôme correspondant à la somme recherchée.
On peut donc définir trois étapes à suivre pour soustraire des polynômes :
-
Regrouper les termes semblables.
-
Soustraire les termes constants.
-
Soustraire les coefficients des termes algébriques semblables.
On peut utiliser le calcul algébrique ou encore la méthode des tuiles algébriques pour effectuer l'addition d'expressions algébriques. Aussi, des vidéos sont disponibles sur ce sujet.
On retient que lors de la soustraction :
-
Seuls les termes semblables peuvent être simplifiés.
-
Ce sont les coefficients de chacun des termes semblables qui sont soustraits.
Il est rare qu'une équation soit formée uniquement par des soustractions. Il faudra, dans ce cas, respecter la priorité des opérations lors de la réduction de l'expression algébrique.
La soustraction de deux polynômes est obtenue en soustrayant les termes semblables des deux polynômes. Le résultat obtenu sera sous forme de polynôme.
Prenons l'expression algébrique suivante :||(2x^3+3x + 2)-(x^3+2x-4)|| Les parenthèses distinguent les deux polynômes que l'on doit soustraire. Afin de les enlever, le négatif devant la deuxième parenthèse doit être distribué à chacun des termes à l'intérieur de la parenthèse.
On obtient alors l'expression suivante : ||2x^3+3x+2\color{red}{-}x^3\color{red}{-}2x\color{red}{+}4|| On peut ensuite réduire l'expression. Pour ce faire, on suit les étapes suivantes :
-
Regrouper les termes semblables (les mêmes lettres affectées des mêmes exposants).||\color{green}{2x^3- x^3}+\color{red}{3x - 2x}+\color{blue}{2 + 4}||
-
Soustraire les termes constants.||\color{green}{2x^3- x^3}+\color{red}{3x - 2x}+\color{blue}{6}||
-
Soustraire les coefficients des termes algébriques semblables.||\color{green}{x^3}+\color{red}{x}+\color{blue}{6}||
La réponse est donc : |x^3+x+6.|
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Selon la loi de la <a href="/fr/eleves/bv/mathematiques/les-proprietes-des-operations-m1060#a3">distributivité</a>, un négatif devant une parenthèse se distribue à chacun des termes situés à l'intérieur de la parenthèse.</p>
</body></html>
Prenons l'expression algébrique suivante : ||(5x^2-11xy+6x-13)-(-2x^2+y^2-8xy+12)||
Les parenthèses distinguent les deux polynômes que l'on doit soustraire. Afin de les enlever, le négatif devant la deuxième parenthèse doit être distribué à chacun des termes à l'intérieur de la parenthèse.
On obtient alors l'expression suivante : ||5x^2-11xy+6x-13+2x^2-y^2+8xy-12||On peut ensuite réduire l'expression. Pour ce faire, on suit les étapes suivantes :
-
Regrouper les termes semblables (les mêmes lettres affectées des mêmes exposants).||\color{green}{5x^2+2x^2}\color{red}{-11xy+8xy}+6x-y^2\color{blue}{-13-12}||
-
Soustraire les termes constants.||\color{green}{5x^2+2x^2}\color{red}{-11xy+8xy}+6x-y^2\color{blue}{-25}||
-
Soustraire les coefficients des termes algébriques semblables.||\color{green}{7x^2}\color{red}{-3xy}+6xy-y^2\color{blue}{-25}||
La réponse est donc : |7x^2-3xy+6x-y^2-25.|
On peut vérifier si l'expression de départ est équivalente à l'expression réduite, on peut remplacer chaque variable par une valeur choisie et calculer la valeur de chaque expression. Si les expressions obtenues sont de même valeur, cela indique qu'elles sont équivalentes.
Si on vérifie le premier exemple ci-dessus: ||(2x^3+3x+2)-(x^3+2x-4)=x^3+x+6|| On choisit une valeur pour les variables. Par exemple, si |x=2|:||\begin{align}2(\color{red}{2})^3+3(\color{red}{2})+2-\color{red}{2}^3-2(\color{red}{2})+4&=(\color{red}{2})^3+\color{red}{2}+6\\ \\
16+6+2-8-4+4&=8+2+6\\ \\
16&=16\end{align}||
Les deux expressions sont donc équivalentes.
Pour aider à mieux visualiser la soustraction de polynômes, on peut la représenter à l’aide des tuiles algébriques. Lorsqu’on utilise les tuiles algébriques, il faut représenter tout d’abord chaque expression algébrique par un assemblage de tuiles. On rassemble par la suite les tuiles identiques et on fait la soustraction de ces tuiles identiques.
Soit les deux polynômes suivants avec leur représentation en tuiles algébriques :
|2x^3+3x+2|
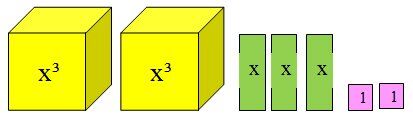
|x^3+2x-4|
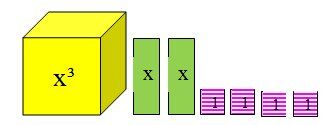
On remarque qu'une valeur positive est représentée par une tuile de couleur pleine alors qu'une valeur négative est plutôt représentée par une tuile hachurée.
La soustraction de ces deux polynômes sera représentée de la façon suivante avec les tuiles algébriques.
|(2x^3+3x+2)-(x^3+2x-4)|
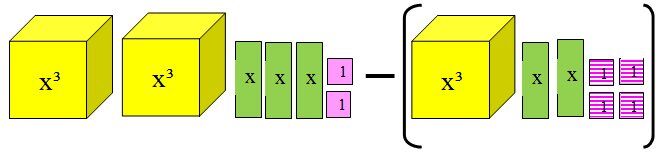
En distribuant le négatif au deuxième polynôme, les valeurs des termes changent de signes.
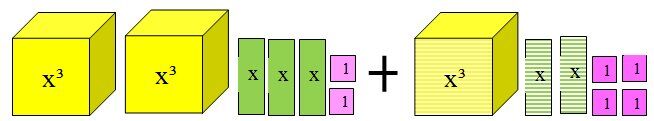
On regroupe maintenant les termes semblables comme lors d’une addition.
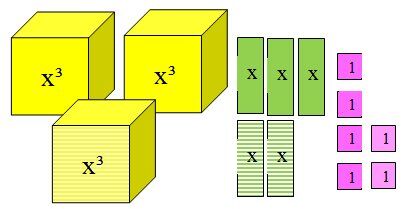
On fait l’addition des tuiles. Une tuile de couleur pleine et une tuile hachurée s’annulent entre elles.
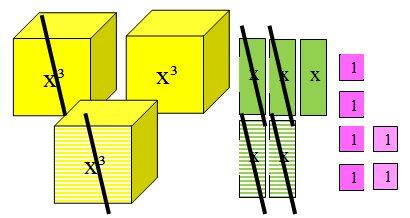
On obtient :
|x^3+x+6|