L'addition de vecteurs par la méthode graphique permet de trouver le vecteur résultant de la combinaison de deux ou plusieurs vecteurs.
Afin d'additionner correctement deux vecteurs, il est important de tenir compte de leur grandeur et de leur orientation. Si on déplace précisément un vecteur sans en modifier sa grandeur ou son orientation, il demeure inchangé. C'est donc cette propriété qui est utilisée dans l'addition de vecteur par la méthode graphique.
Selon les manuels et la méthode d'enseignement, cette technique peut être nommée méthode du triangle (s'il n'y a que deux vecteurs) ou méthode du polygone (s'il y a trois vecteurs ou plus). L'expression méthode graphique utilisée dans cette fiche inclut ces deux méthodes.
L'addition de vecteurs se fait toujours en suivant une procédure simple.
- Représenter un système de référence afin de déterminer la position de l'origine.
- Placer le vecteur de façon à ce que l'origine du vecteur soit placée à l'origine du plan cartésien.
- Placer le deuxième vecteur (et les suivants) de façon à ce que l'origine du deuxième vecteur soit située à l'extrémité du premier vecteur.
- Tracer le vecteur résultant, qui correspond au vecteur ayant pour origine le point d'origine du plan cartésien et comme extrémité la pointe de la flèche du dernier vecteur représenté.
- Mesurer la grandeur du vecteur résultant et déterminer son orientation.
Addition de deux vecteurs
Quelle est la somme des vecteurs représentés ci-dessous ?
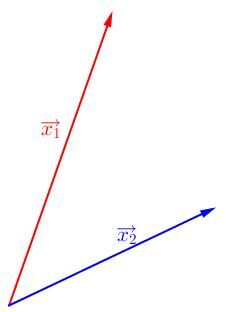
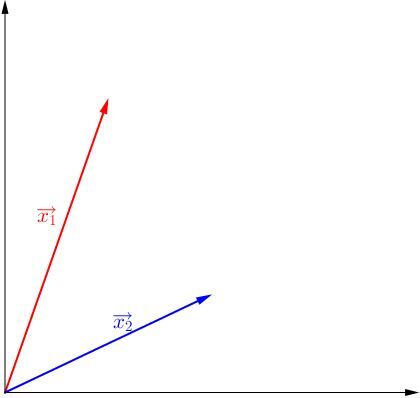
Il faut tout d'abord placer un système de référence.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
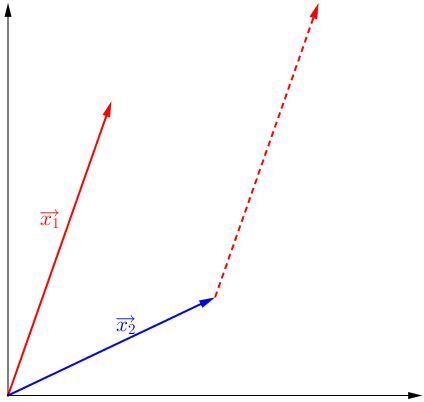
<html><body><p>Ensuite, il faut déplacer les deux vecteurs un à la suite de l'autre. Puisque l'addition est <a href="/fr/eleves/bv/mathematiques/les-proprietes-des-operations-m1060#commutativite">commutative</a>, on peut déplacer le vecteur rouge à l'extrémité du vecteur bleu, ou le vecteur bleu à l'extrémité du vecteur rouge, et le résultat sera le même.</p>
</body></html>
Il faut ensuite tracer le vecteur résultant en partant de l'origine du système de référence jusqu'à la fin du dernier vecteur.
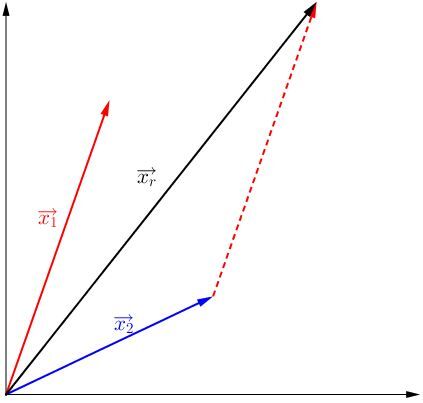
Pour déterminer la grandeur du vecteur résultant, il faut mesurer le vecteur avec une règle.
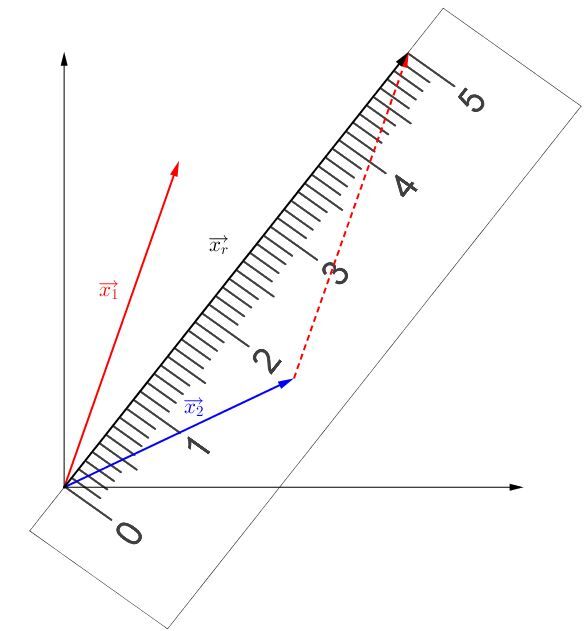
Pour connaître son orientation, il faut prendre son rapporteur d'angles.
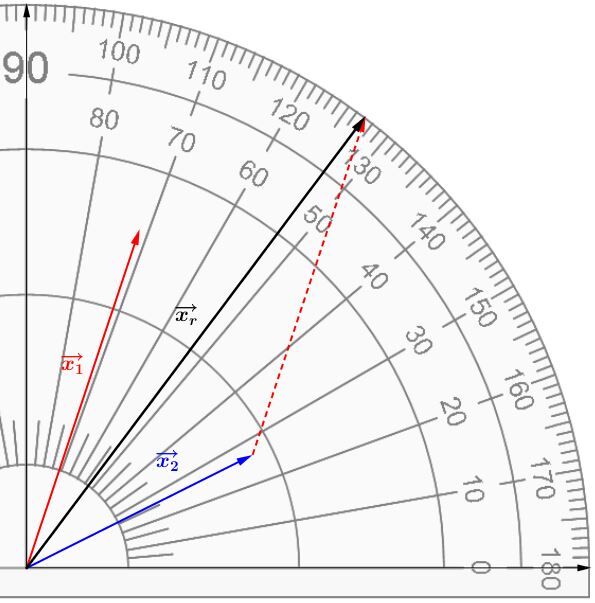
Le vecteur résultant de l'addition des deux vecteurs a une grandeur de |\text {5 u}| et une orientation de |53^{\circ}|.
Addition de trois ou plusieurs vecteurs
Si plusieurs vecteurs doivent être additionnés ensemble la même technique est utilisée pour trouver le vecteur résultant.
