<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span class="ms-rteStyle-bv-tableaudefinition">La <strong>relation entre la vitesse et le temps dans le MRUA</strong> est décrite par une relation linéaire où <a href="/fr/eleves/bv/physique/la-vitesse-p1081">la vitesse</a> augmente d'un taux constant pour la durée totale du mouvement.</span></p>
</body></html>
Pour observer cette relation, il est possible de représenter graphiquement des valeurs de la vitesse d'un objet en fonction du temps.
On considère le mouvement d'une voiture qui se met en mouvement après avoir fait un arrêt obligatoire. On note la vitesse de cette voiture à différents moments.
Vitesse d'une voiture en fonction du temps
| Temps |\small \text {(s)}| | Vitesse |\small \text {(m/s)}| |
| 0 | 0 |
| 10 | 2,5 |
| 20 | 5,0 |
| 30 | 7,5 |
| 40 | 10,0 |
On peut représenter la vitesse de la voiture en fonction du temps dans le graphique ci-dessous.
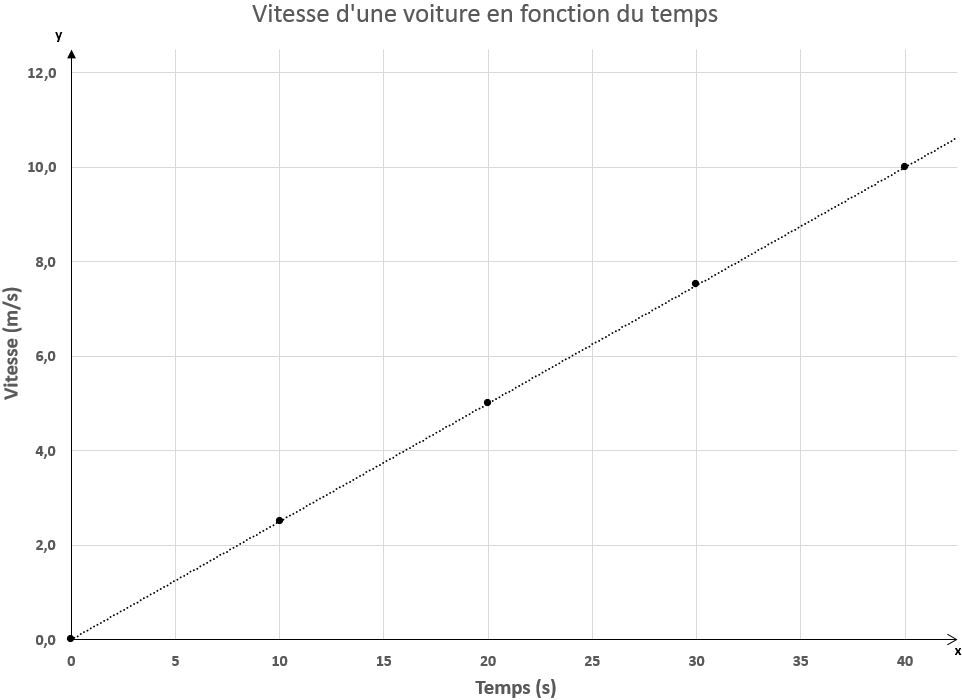
La relation obtenue est une fonction linéaire, ce qui signifie que la vitesse augmentera de manière constante.
On peut également considérer la situation inverse, soit une voiture qui se freine afin de s'arrêter à un arrêt obligatoire. On note la vitesse de cette voiture à différents moments.
Vitesse d'une voiture en fonction du temps
| Temps |\small \text {(s)}| | Vitesse |\small \text {(m/s)}| |
| 0 | 12,5 |
| 10 | 10,0 |
| 20 | 7,5 |
| 30 | 5,0 |
| 40 | 2,5 |
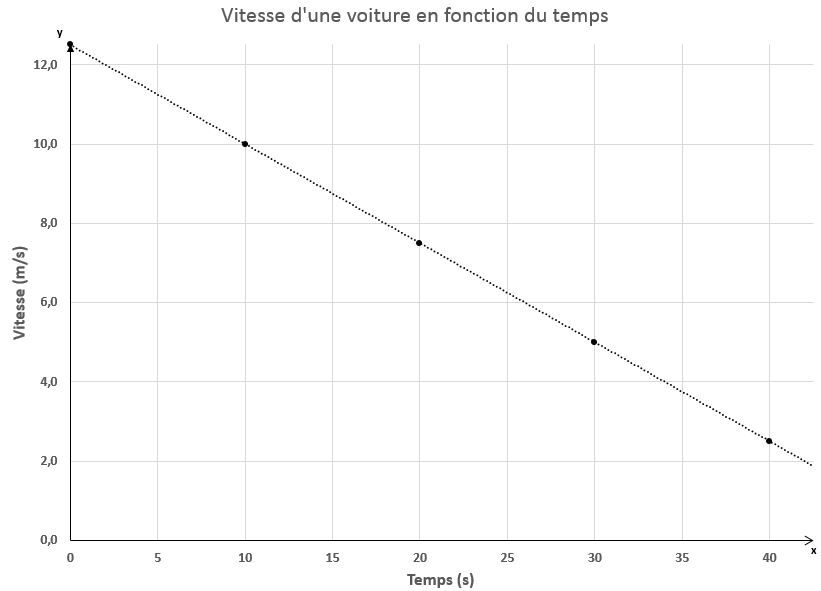
On peut représenter la vitesse de la voiture en fonction du temps dans le graphique ci-dessous.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span><span>La relation obtenue est également une fonction linéaire: toutefois, celle-ci étant négative, ce qui signifie que la vitesse diminuera de manière constante.</span></span></p>
<p>Si on calculait la pente de ces graphiques, la valeur obtenue serait égale à celle de l'<a href="/fr/eleves/bv/physique/l-acceleration-p1082">accélération</a>. Puisque le graphique obtenu est une droite, on déduit donc que l'accélération est constante.</p>
</body></html>
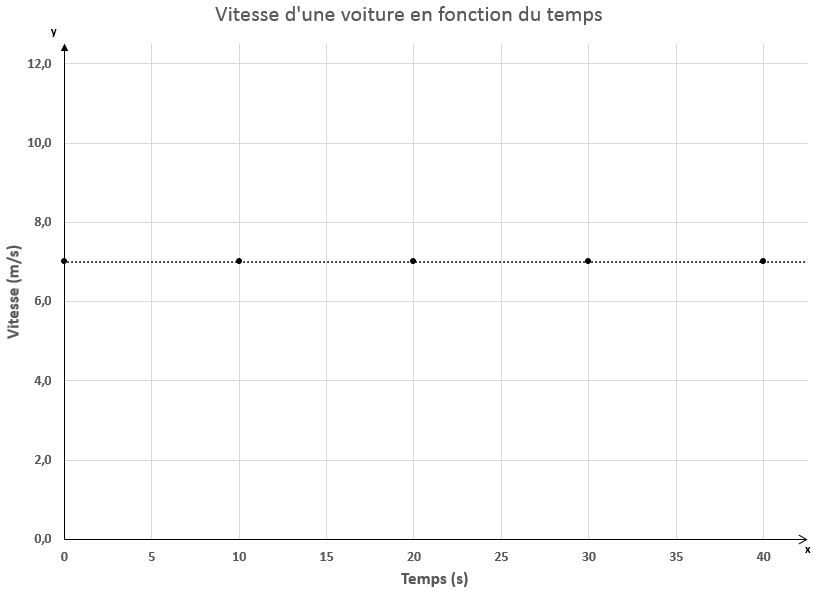
Si la droite obtenue avait été dessinée à l'horizontale, l'accélération aurait été nulle et la vitesse constante, comme dans un MRU.
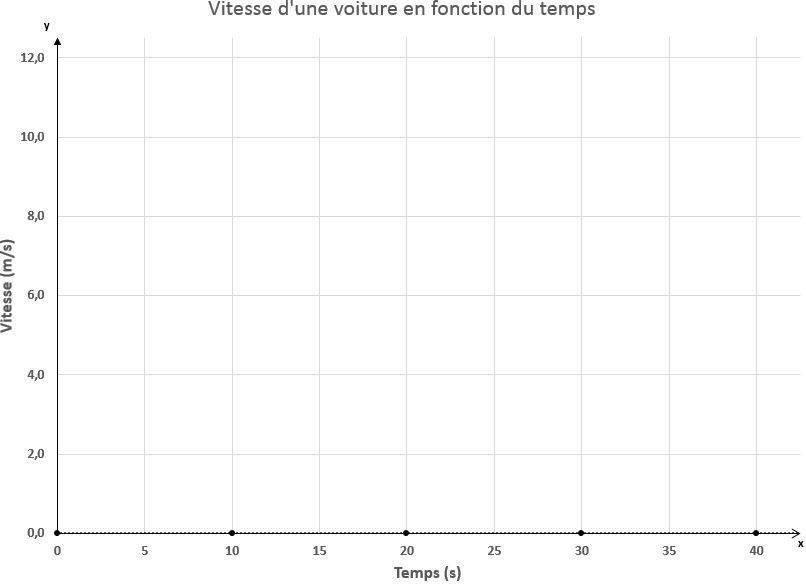
De plus, une droite horizontale superposée à l'axe des abscisses ne représente pas un MRUA, puisque l'objet en mouvement est immobile.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Pour déterminer la variation de position de la voiture durant un intervalle de temps, l'aire sous la courbe permettrait d'obtenir simplement la distance parcourue durant un tel intervalle. Cette technique s'applique dans n'importe quel graphique de <a href="/fr/eleves/bv/physique/la-vitesse-p1081">vitesse</a>.</p>
</body></html>
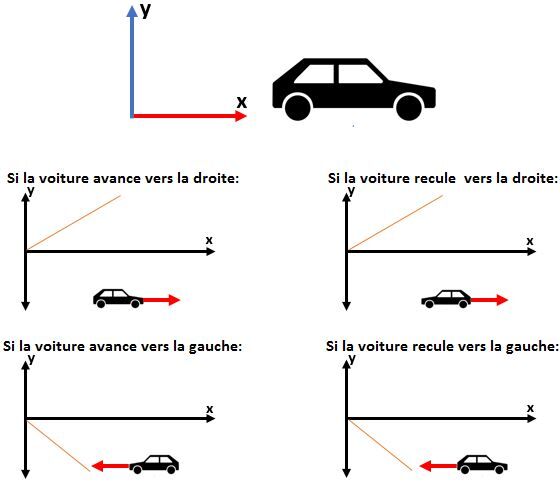
Pour savoir si la vitesse est positive ou négative, il est important de vérifier le sens du mouvement et non le type de mouvement. Par exemple, une voiture qui recule dans la direction indiquée par le système de référence aura une vitesse positive.
Pour valider ta compréhension à propos du MRUA de façon interactive, consulte la MiniRécup suivante :

La relation entre la vitesse et le temps dans le MRUA se distingue de la relation entre la vitesse et le temps dans le MRU.