La vitesse est le rapport entre la variation de la position d'un mobile et le temps nécessaire pour faire ce changement de position.
Des mesures de vitesse sont prises quotidiennement, entre autres, lors de déplacements en voiture ou en autobus. Dans ces cas, la vitesse est mesurée en kilomètres par heure |\small \text {(km/h)}|. Toutefois, dans les formules utilisées en physique, l'unité de mesure privilégiée est le mètre par seconde |\small \text {(m/s)}|.
L'équation générale utilisée pour calculer la vitesse est:
|v=\displaystyle \frac{\triangle x}{\triangle t}|
où
|v| représente la vitesse du mobile |\small \text {(en m/s)}|
|\triangle x| représente la variation de position du mobile |\left( x_{f} - x_{i} \right)| |\small \text {(en m)}|
|\triangle t| représente la variation de temps |\left( t_{f} - t_{i} \right)| |\small \text {(en s)}|
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>La formule présentée dans l'encadré ci-dessus est similaire au calcul de la pente d'une droite dans un graphique. En effet, en traçant le graphique de la position d'un mobile en fonction du temps, le calcul de la pente de ce graphique permet de déterminer la vitesse du mobile.</p>
<p>D'un point de vue graphique, trois types de relation peuvent être obtenus:</p>
<table cellspacing="0" class="ms-rteTable-default">
<tbody>
<tr class="ms-rteTableEvenRow-default">
<td class="ms-rteTableEvenCol-default text-align-left" style="width:50%;">Si le graphique de la vitesse en fonction du temps donne une relation nulle, l'objet se déplace à vitesse constante. L'objet se déplace donc dans un <a href="/fr/eleves/bv/physique/le-mouvement-rectiligne-uniforme-mru-p1004">mouvement rectiligne uniforme (MRU)</a>.</td>
<td class="ms-rteTableOddCol-default text-align-left" style="width:50%;">
<p><span id="DeltaPlaceHolderMain"><img alt="graphique" data-entity-type="file" data-entity-uuid="86727c15-0902-48ee-99bf-884d3af27266" src="/sites/default/files/inline-images/p1081i1.jpg"></span></p>
</td>
</tr>
<tr class="ms-rteTableOddRow-default">
<td class="ms-rteTableEvenCol-default text-align-left" rowspan="1">Si le graphique de la vitesse en fonction du temps donne une relation linéaire, l'objet accélère (ou décélère). L'objet se déplace donc en faisant un <a href="/fr/eleves/bv/physique/le-mouvement-rectiligne-uniformement-accelere-p1006">mouvement rectiligne uniformément accéléré (MRUA)</a>.</td>
<td class="ms-rteTableOddCol-default text-align-left" rowspan="1">
<p><img alt="graphique" data-entity-type="file" data-entity-uuid="a04d7752-ba83-491a-8978-9a75f4e7e739" src="/sites/default/files/inline-images/p1081i2.jpg"></p>
</td>
</tr>
<tr class="ms-rteTableEvenRow-default">
<td class="ms-rteTableEvenCol-default text-align-left"><span id="DeltaPlaceHolderMain">Si le graphique de la vitesse en fonction du temps donne une relation nulle superposée à l'axe des abscisses, l'objet est immobile.</span></td>
<td class="ms-rteTableOddCol-default text-align-left"><img alt="graphique" data-entity-type="file" data-entity-uuid="cc90d196-d9dc-446a-99d2-5623de0ed13f" src="/sites/default/files/inline-images/p1081i8.jpg"></td>
</tr>
</tbody>
</table>
</body></html>
Il existe deux types de vitesse qui peuvent être déterminés à partir d'un graphique:
Pour convertir des mètres par seconde en kilomètres par heure, il faut suivre la procédure suivante:
|\displaystyle \frac{\text {m}}{\text {s}} \times \frac {1 \text { km}}{1000 \text { m}} \times \frac {3600 \text { s}}{\text {h}}|
De manière plus simple, il suffit de faire:
|\displaystyle \frac{\text {m}}{\text {s}} \times 3,6 = \frac{\text {km}}{\text {h}}|
Il est également possible de convertir des kilomètres par heure en mètres par seconde.
|\displaystyle \frac{\text {km}}{\text {h}} \times \frac {1000 \text { m}}{\text { km}} \times \frac {1 \text { h}}{3600 \text { s}}|
De manière plus simple, il suffit de faire:
|\displaystyle \frac{\text {km}}{\text {h}} \div 3,6 = \frac{\text {m}}{\text {s}}|
La vitesse moyenne d'un mobile est le rapport entre son déplacement et le temps écoulé.
La vitesse moyenne n'est pas nécessairement uniforme entre le début et la fin du déplacement : elle représente ce que devrait être la vitesse entre le point de départ et le point d'arrivée si la vitesse était la même tout le long du parcours.
Une voiture arrêtée à un panneau de signalisation accélère après avoir fait son arrêt obligatoire. On représente dans un graphique sa position en fonction du temps. Quelle est la vitesse moyenne de la voiture durant les cinq premières secondes de son déplacement?
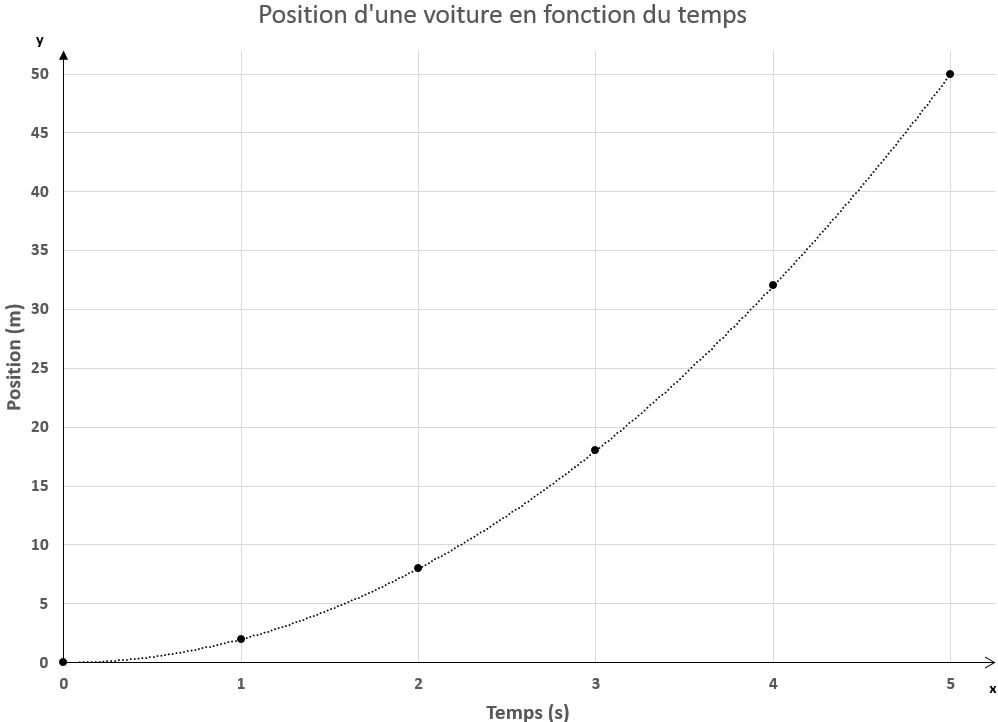
Pour déterminer la vitesse, il faut déterminer la variation de position et la variation de temps. La variation de temps est connue, puisque la voiture s'est déplacée durant cinq secondes. En observant le graphique, le dernier point indique qu'après cinq secondes, la voiture a parcouru |\text {50 m}|. En utilisant la formule de la vitesse, on obtient donc :
||\begin{align}v = \displaystyle \frac {\triangle x}{\triangle t} \quad \Rightarrow \quad
v &= \displaystyle \frac {50 \: \text{m} - 0 \: \text{m}}{5 \: \text{s} - 0 \: \text{s}} \\
&= 10 \: \text{m/s} \end{align}||
La voiture a donc roulé avec une vitesse moyenne de |10 \: \text {m/s}| durant les cinq premières secondes de son déplacement.
Dans l'exemple ci-dessus, la vitesse moyenne de la voiture était de |\small 10 \: \text {m/s}|. Toutefois, il est important de noter que la voiture n'a pas toujours roulé à |\small 10 \: \text {m/s}|: au départ, puisque la voiture était arrêtée, sa vitesse était nulle. Ceci signifie que la vitesse de la voiture après cinq secondes était plus grande que |\small 10 \: \text {m/s}| afin que la moyenne de la vitesse puisse donner la valeur calculée.
Si on veut déterminer la vitesse à un moment précis, il faut utiliser un autre calcul de vitesse, soit celui de la vitesse instantanée.
La vitesse instantanée est la vitesse à un instant précis du déplacement d'un mobile.
En regardant l'indicateur de vitesse d'une voiture, il est possible de déterminer la vitesse instantanée de cette voiture. Cette mesure sert donc uniquement à déterminer à quelle vitesse la voiture roule au moment où la vitesse est observée. Il est impossible de savoir quelle sera la vitesse de la voiture pour un grand déplacement.
Le calcul d'une vitesse instantanée se fait en traçant la pente d'un graphique de la position en fonction du temps.
Si le graphique de la position en fonction du temps est une relation linéaire, le calcul de la vitesse instantanée se fait en déterminant la pente de ce graphique.
Détermine la vitesse instantanée à la troisième seconde du mouvement de la voiture
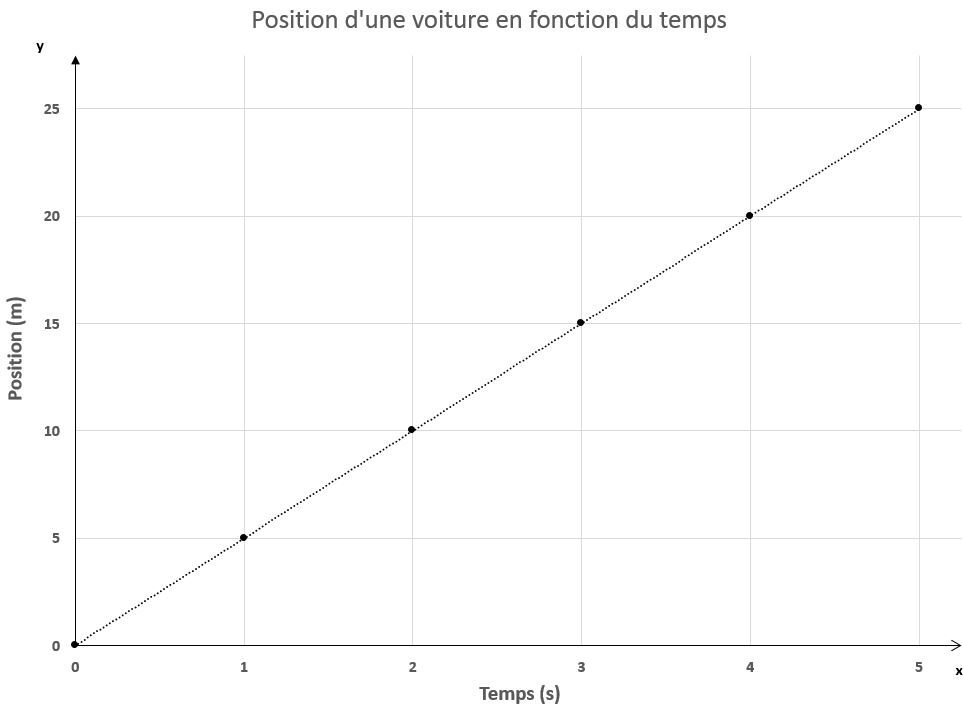
En dessinant la pente de ce graphique, celle-ci se superpose à la droite utilisée pour calculer la vitesse moyenne. Ainsi, lorsqu'un graphique de position en fonction du temps donne une relation linéaire, la vitesse moyenne et la vitesse instantanée sont identiques.
Pour calculer la vitesse instantanée:
||\begin{align}v = \displaystyle \frac {\triangle x}{\triangle t} \quad \Rightarrow \quad
v &= \displaystyle \frac {15 \: \text{m} - 0 \: \text{m}}{3 \: \text{s} - 0 \: \text{s}} \\
&= 5 \: \text{m/s} \end{align}||
Dans un graphique représentant la position en fonction du temps, une ligne courbe représente une accélération ou un changement de vitesse. Il est possible de calculer une vitesse instantanée à l’aide de la tangente de la courbe à un point donné. Une tangente est une droite passant par un seul point de la courbe.
Détermine la vitesse instantanée à la troisième seconde du mouvement de cette voiture.
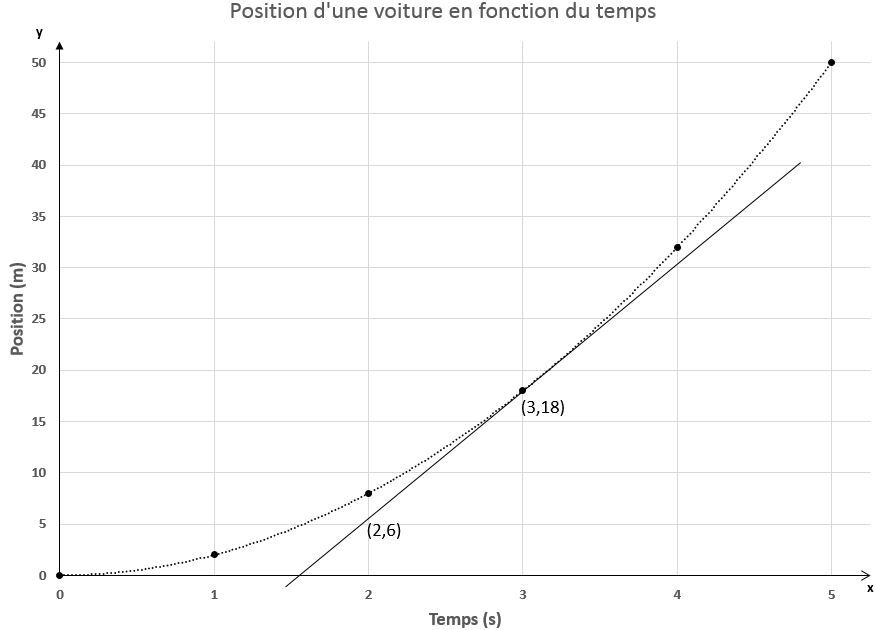
Pour déterminer la vitesse instantanée, il faut dessiner la tangente de la courbe au point désiré, soit à trois secondes. Par la suite, il faut identifier deux points sur cette droite et calculer la vitesse instantanée en utilisant la formule de la vitesse. Par exemple, prenons les points |( (2,6) et (3,18) )| sur la tangente dans le graphique ci-dessus.
||\begin{align}v = \displaystyle \frac {\triangle x}{\triangle t} \quad \Rightarrow \quad
v &= \displaystyle \frac {18 \: \text{m} - 6 \: \text{m}}{3 \: \text{s} - 2 \: \text{s}} \\
&= \displaystyle \frac {12 \: \text{m}}{1 \: \text{s}}\\
&= 12 \: \text{m/s} \end{align}||
La vitesse moyenne, déterminée auparavant, pour cette voiture lors de ce déplacement était de |\small \text {10 m/s}|. À la suite du calcul de la vitesse instantanée, il est possible de noter que dès la troisième seconde, la vitesse instantanée est en réalité supérieure à cette vitesse moyenne.
Le graphique de la vitesse en fonction du temps nous informe de la vitesse d’un mobile à tout moment. On ne peut pas savoir où se trouve l’objet par un simple regard sur le graphique: toutefois, on peut déterminer sa vitesse et l'orientation du mouvement.
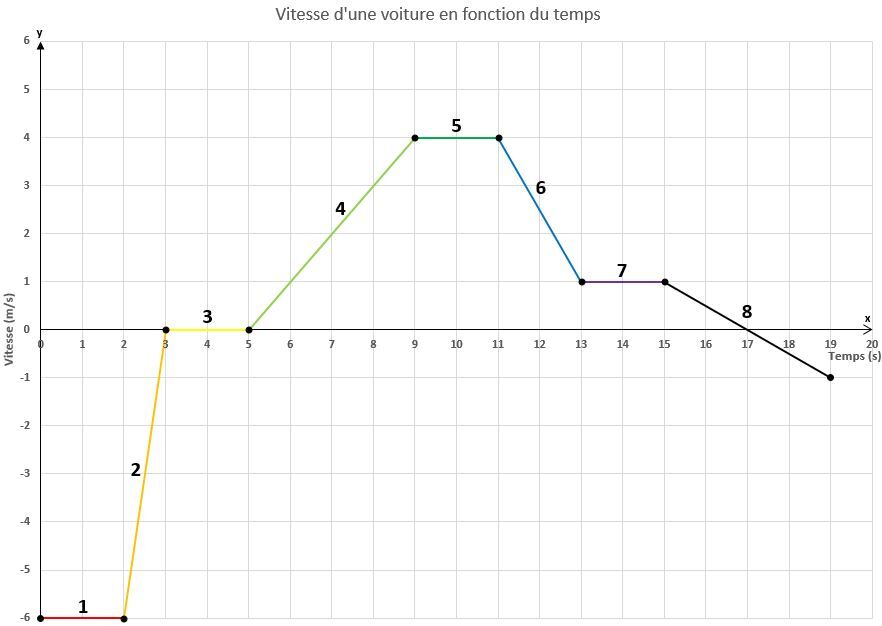
- Dans le premier segment, l'objet se déplace à vitesse constante. La vitesse négative signifie que l'objet se déplace dans le sens contraire aux références fournies au départ. Par exemple, si un objet se déplaçant vers le haut a une vitesse positive, l'objet ayant une vitesse semblable à celle du segment 1 se déplacerait vers le bas.
- La vitesse de l'objet diminue de manière constante. L'objet décélère donc durant une seconde. En calculant l'aire sous la courbe, il est possible de déduire que l'objet a parcouru |\small \text {3 m}|.
- Entre la troisième et la cinquième seconde, la vitesse est constante. Toutefois, la droite est superposée à l'axe des abscisses. Ceci signifie que l'objet ne change pas de position durant ces deux secondes: il est donc immobile.
- L'objet accélère à nouveau durant le quatrième segment. Alors que sa vitesse était nulle au départ, il atteint une vitesse de |\small \text {4 m/s}| quatre secondes plus tard, ce qui donne une accélération de |\small \text {1 m/s}^2|. En comparant cette droite avec celle du segment 2, il est possible de noter que l'accélération du segment 4 est plus petite que l'accélération du segment 2, car l'inclinaison de la pente est plus faible. Or, plus l’inclinaison est prononcée, plus l’accélération est grande.
- Bien que la vitesse soit constante durant le cinquième segment, elle n'est pas nulle. Durant ces deux secondes, l'objet conservera une vitesse constante de |\small \text {4 m/s}|.
- Durant le sixième segment, la vitesse de l'objet diminue de manière constante. Il ralentira, sans jamais s'arrêter, durant une période de deux secondes.
- L'objet conserve la vitesse qu'il avait à la fin du segment précédent. Il n'est pas immobile, car la droite de la vitesse n'est pas superposée à l'axe horizontal.
- Finalement, durant ce dernier segment, la vitesse de l'objet diminue. L'objet subit donc une accélération négative. En effet, la pente du graphique est négative. Entre la 15e et la 17e seconde, la valeur de la vitesse est toujours positive (au-dessus de l'axe des |x|), ce qui veut dire que l'objet se dirige vers le haut, mais elle diminue jusqu'à ce qu'elle atteigne |0\ \text{m/s}.| Entre la 17e et la 19e seconde, la valeur de la vitesse est négative (sous l'axe des |x|), ce qui veut dire que l'objet a changé de direction et se dirige vers le bas. Sa vitesse devient de plus en plus négative, ce qui veut dire que l'objet se dirige vers le bas avec une plus grande vitesse.
Dans un graphique de vitesse en fonction du temps, l’aire sous la courbe indique la distance que l'objet a parcourue à l’intérieur d'un intervalle de temps.
Calcule la variation de position entre la 11e et la 13e seconde.
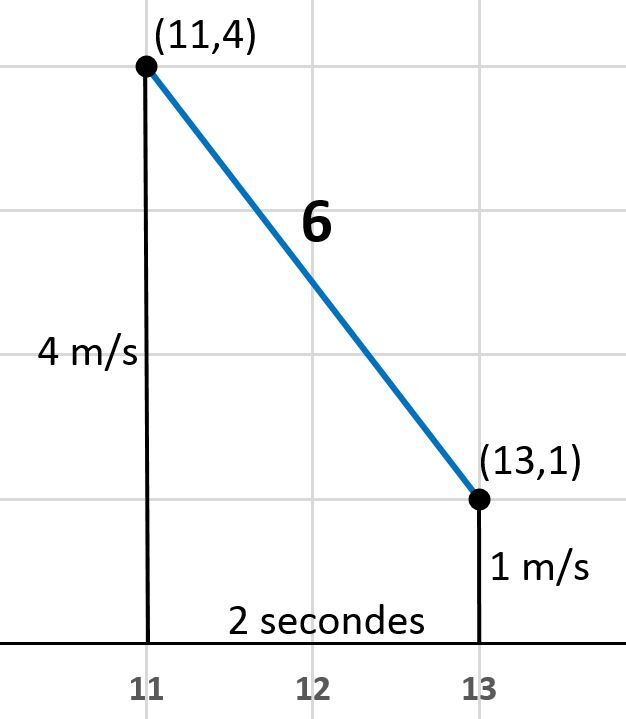
L'aire sous la courbe entre la 11e et la 13e seconde a la forme d’un trapèze. Il faut donc utiliser la formule de l’aire d’un trapèze pour déterminer l’aire sous la courbe.
||\begin{align}A = \displaystyle \frac{(B + b)\times h}{2}
\quad \Rightarrow \quad
A &= \displaystyle \frac{(4 \: \text{m/s}+ 1 \: \text{m/s})\times 2 \: \text{s}}{2} \\
&= 5 \: \text{m} \end{align}||
La variation de position de l’objet entre la onzième et la treizième seconde est de |\text {5 m}|.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Lorsque l’aire sous la courbe représente une zone sous l’axe des x, on calculera un déplacement négatif. Cette valeur négative est logique, puisque sous l’axe des x, la vitesse est négative. On se déplacera du côté négatif si la vitesse est négative. Il est donc très important d'établir <a href="/fr/eleves/bv/physique/le-systeme-de-reference-p1001">un système de référence</a> clair au début d'un problème.</p>
</body></html>