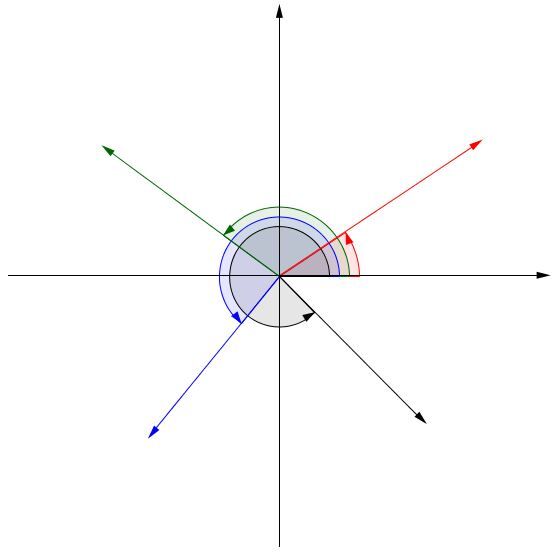
Afin d'additionner deux vecteurs, il est possible d'en additionner les composantes. En effet, un vecteur peut se décomposer en deux composantes, soit une composante horizontale parallèle à l'axe des abscisses et une composante verticale parallèle à l'axe des ordonnées.
Lorsque la grandeur et l'orientation du vecteur sont connues, il est possible de déterminer les composantes de ce vecteur en utilisant les relations trigonométriques.
Pour déterminer les composantes d'un vecteur, on utilise les règles suivantes:
||x=r\times \cos \theta||||y=r\times \sin \theta||
|r| représente la grandeur du vecteur
|\theta| représente l'orientation du vecteur
Un vecteur mesure |\small \text {3 u}| et il est orienté à |\small 30^{\circ}|. Quelles sont les composantes de ce vecteur ?
||\begin{align} x=r\times \cos \theta \quad \Rightarrow \quad
x &= 3\times \cos 30^{\circ} \\
&= 2,60 \: \text {u} \end{align}||
||\begin{align} y=r\times \sin \theta \quad \Rightarrow \quad
y &= 3\times \sin 30^{\circ} \\
&= 1,50 \: \text {u} \end{align}||
Les composantes de ce vecteur sont donc |2,60 \: \text {u}| sur l'axe des abscisses (ou axe des x), et |1,50 \: \text {u}| sur l'axe des ordonnées (axe des y).
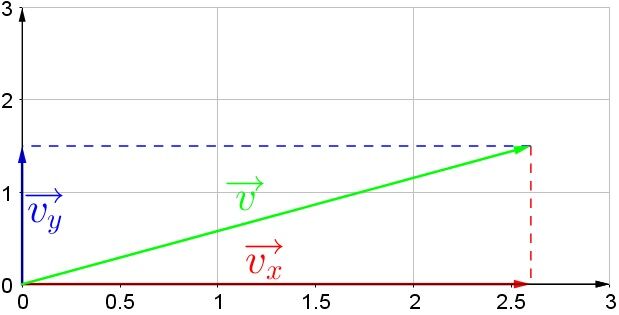
Si un vecteur est illustré dans un plan cartésien, il faut reporter les dimensions du vecteur sur chacun des axes afin d'en trouver les composantes.
Quelle est la grandeur et l'orientation du vecteur illustré ci-dessus ?
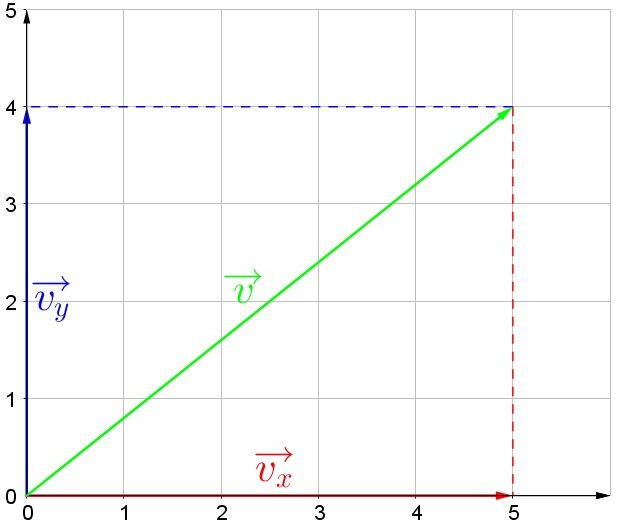
En reportant le vecteur sur les axes (en pointillés rouge et bleu), le vecteur a une composante horizontale de |5 \: \text {u}| et une composante verticale de |4 \: \text {u}|.
Pour valider ta compréhension à propos de la décomposition de vecteurs de façon interactive, consulte la MiniRécup suivante :

Lorsque les composantes d'un vecteur sont connues, il est possible de déterminer la grandeur en utilisant la relation de Pythagore. Pour déterminer l'angle, les rapports trigonométriques peuvent être utilisés.
Pour passer des composantes horizontales |(x, y)| en un vecteur ayant une grandeur |(r)| et une orientation |(\theta)|, on utilise les règles suivantes:
|| r = \sqrt{x^2 + y^2}|||| \theta=\tan^{-1}\left(\begin{array}{c}\displaystyle \frac{y}{x} \end{array}\right)||
Quelle est la grandeur et l'orientation du vecteur illustré ci-dessus ?
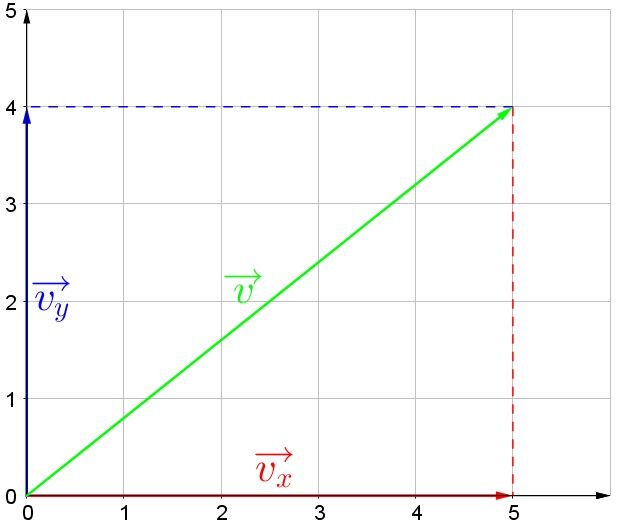
|| \begin{align} r = \sqrt{\color{red} {x}^2 + \color{blue} {y}^2} \quad \Rightarrow \quad r &= \sqrt{\color{red} {5^2} + \color{blue} {4^2}} \\ &= \sqrt{41}\\ & \approx 6,40 \: \text{u} \end{align}||
||\begin{align} \theta=\tan^{-1} \left( \frac{\color{blue} {y}}{\color{red} {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} = \left( \frac{\color{blue} {4}}{\color{red} {5}} \right)\\ &= \tan^{-1}\left(0,8\right)\\ & \approx 38,7^{\circ}\end{align}||
Le vecteur résultant a une grandeur de |\text {6,40 u}| et il est situé à |38,7^{\circ}| par rapport à l'axe des abscisses.
Pour déterminer la valeur de l’angle |\theta|, il faut déterminer la valeur de l’angle entre l’axe des abscisses positif (axe des x positif), qui est le point de départ, et le vecteur déterminé à l’étape précédente.