Collision theory states that the rate of a chemical reaction depends on the number of collisions between the reactant particles, their orientation and the kinetic energy level.
Collision theory is based on three principles. In order for a chemical reaction to occur:
-
Particles of reactants must collide with each other.
-
Particles of reactants must collide in a specific orientation.
-
Particles of reactants must have a kinetic energy |(E_k)| equal to or above the activation energy |(E_a)| required to form an activated complex.
Collisions between particles of reactants in optimal orientation and with sufficient energy are considered to be successful and are often called effective, fruitful or inelastic.
The rate of a chemical reaction is directly proportional to the number of inelastic collisions.
The collisions between particles of reactants are required in order for a chemical reaction to occur. The more collisions there are in general, the more inelastic collisions will occur. The number of inelastic collisions depends on:
-
the nature and state of the reactants
-
the concentration
-
the surface area between the reactants
-
the temperature
-
the presence of a catalyst
When particles collide at the wrong angle, they bounce away from each other without any changes to their bonds. When particles collide at an optimal angle, an activated complex can form and a chemical reaction is possible.
Consider the following analogy: chopping wood with an ax requires the ax to be oriented in a specific way. If a log is hit by the flat side of the ax, it cannot split.
The following images show collisions between the same reactant particles in different orientations.
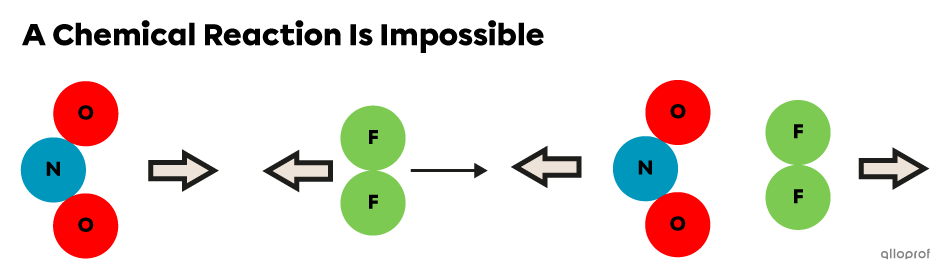
The orientation of reactants (|\text{NO}_2| and |\text{F}_2|) is not optimal, so they collide and bounce back without changes to their structure.
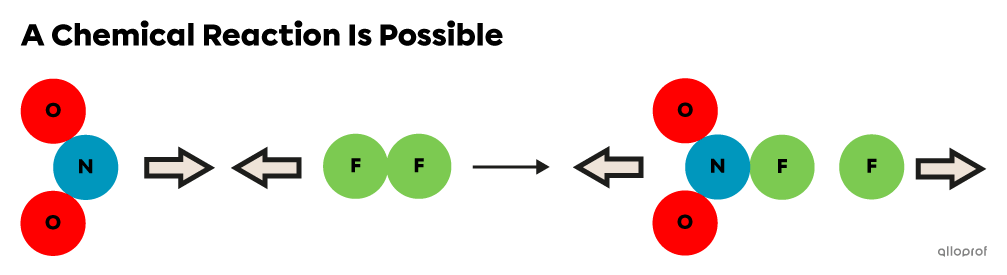
The orientation of the reactants (|\text{NO}_2| and |\text{F}_2|) is optimal, so when they collide, products can form.
In order for a chemical reaction to occur, an input of energy is necessary to break the chemical bonds between the atoms of the reactants. The kinetic energy of colliding particles serves as this energy input.
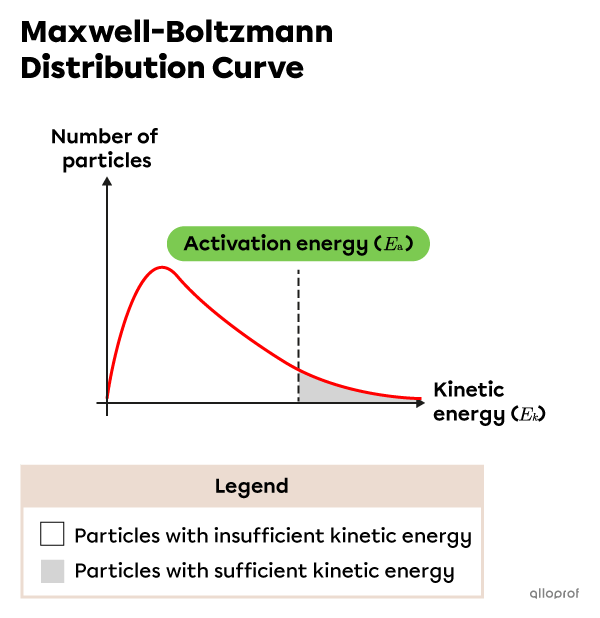
According to the Maxwell-Boltzmann distribution curve, particles of a substance have different speeds at a given temperature. Since kinetic energy |E_k| is proportional to the square of a particle’s speed, this curve can be used to show the distribution of particles’ |E_k.|
As shown in the following distribution curve, many particles do not have enough |E_k| to match the |E_a.| Collisions between these particles do not lead to chemical reactions. Only the particles in the shaded region have enough |E_k| to form an activated complex and undergo a chemical reaction.
Particles with insufficient |E_k| bounce away from each other, even if they are correctly oriented. Their |E_k| is conserved after a collision, so it is referred to as an elastic collision. Optimally oriented particles with sufficient |E_k| undergo inelastic collisions and form an activated complex. Due to energy transformations, the |E_k| of the products is different from reactants.
Following the wood chopping analogy, if an ax is placed on the log gently at low speed, the log will not split, even if the ax is oriented properly. It has to be hit by the wedge at high speed for a successful split.
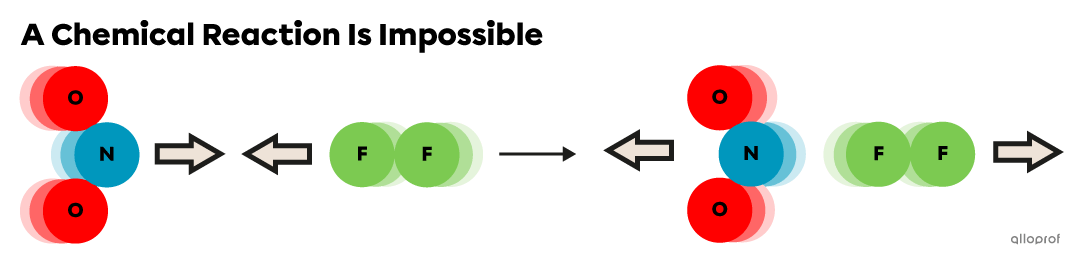
When the |E_k| of the reactants |(\text{NO}_2| and |\text{F}_2)| is below the |E_a| required for this reaction, they undergo elastic collisions: they bounce away and conserve their |{E}_k.|
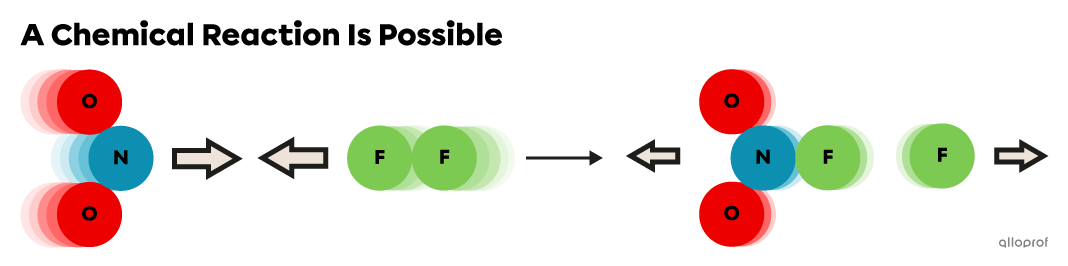
When the |{E}_k| of the reactants (|\text{NO}_2| and |\text{F}_2|) is equal to or above the |{E}_a| required for this reaction, they undergo inelastic collisions and products form.
Collision theory explains complex reactions by analyzing the elementary reactions in the reaction mechanism.
-
A reaction mechanism is a series of elementary reactions through which reactants are transformed into products.
-
An elementary reaction is a single step during a chemical reaction.
-
A simple reaction consists of one elementary reaction.
-
A complex reaction, or a multistep reaction, consists of two or more elementary reactions and involves the formation of at least one reaction intermediate.
-
A reaction intermediate, or simply intermediate, is a substance that forms at the end of an elementary reaction of a reaction mechanism but is not part of the overall reaction.
-
An overall reaction is the chemical equation representing only the reactants and the products formed by the end of a complex chemical reaction.
Simple reactions occur in one step. In other words, a single inelastic collision between the particles of reactants leads to the formation of a single activated complex, followed by the products.
In a simple reaction, when the reactant particles undergo a successful collision, a single activated complex forms. This complex has the highest enthalpy during the chemical reaction.
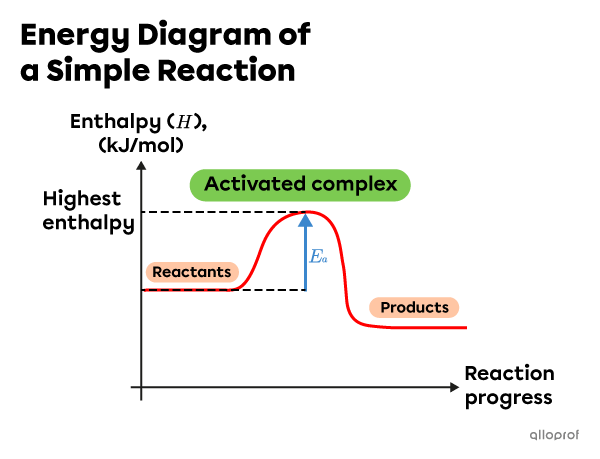
Note: In this energy diagram, the enthalpy of the products is lower than the enthalpy of the reactants. This is an exothermic reaction.
Often, three or more particles must collide to eventually form the products. It is extremely unlikely that all particles can collide simultaneously in optimal orientation and with sufficient kinetic energy. Instead, the reaction mechanism of a complex reaction takes place through multiple elementary reactions where only two particles collide at a time. This is why complex reactions are often called multistep reactions.
In a reaction mechanism of a complex reaction, each elementary reaction has its own |E_a,| activated complex, enthalpy change and reaction rate.
A temporary substance, called a reaction intermediate or a transition state, forms at the end of each elementary reaction. The intermediate is then consumed in the next elementary reaction and does not appear in the overall reaction.
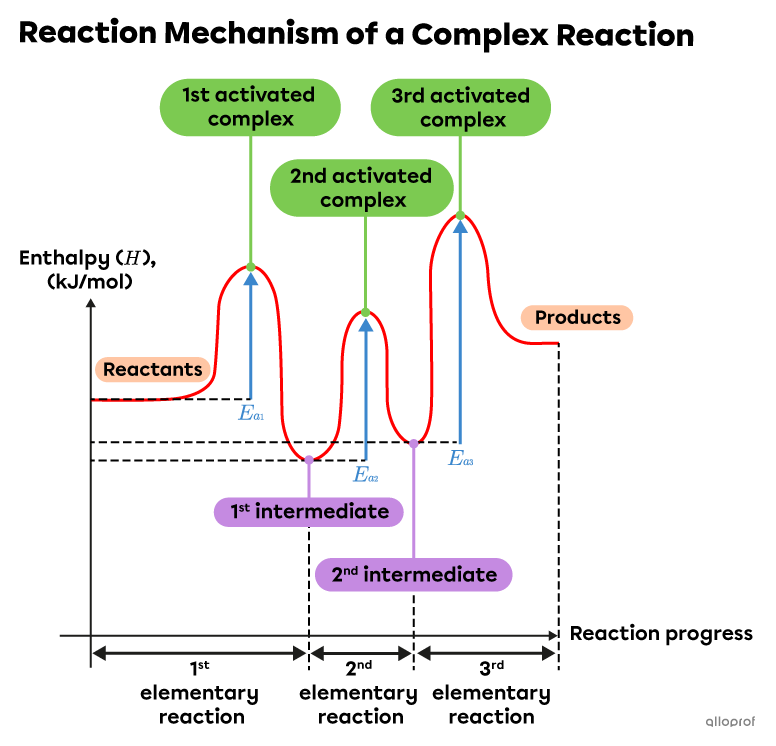
The reaction mechanism of this multistep reaction includes three elementary reactions, as indicated by the formation of three activated complexes and two intermediates. Each complex has its own activation energy.
Note: In this case, the enthalpy of the products is higher than the enthalpy of the reactants. This is an endothermic reaction.
In complex reactions, the rate of the overall reaction depends on the rate of its slowest elementary reaction. Therefore, the slowest elementary reaction in a reaction mechanism is known as the rate-determining step. On an energy diagram, this step can be recognized by the highest activation energy |(E_a).|The overall reaction rate cannot progress faster than the rate-determining step.
Some textbooks define the rate-determining step as the step during which the activated complex has the highest enthalpy. However, the rate-determining step is actually the step with the highest activation energy |(E_a).|
Consider the following reaction mechanism.
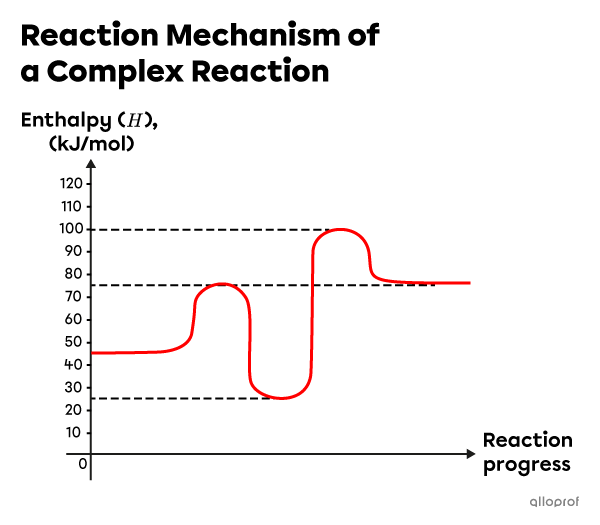
-
Determine the number of elementary reactions required for the reactants to transform into products.
-
Determine the enthalpy of the reaction intermediate(s).
-
Determine the activation energy of each step of the reaction mechanism.
-
Identify the rate-determining step.
Let’s identify the missing information on the reaction mechanism graph and use it to answer the questions. It can be useful to label the following :
-
Reactants
-
Products
-
Activated complex(es)
-
Intermediate(s)
-
Elementary reactions
-
Activation energy |(E_a)| of each elementary reaction
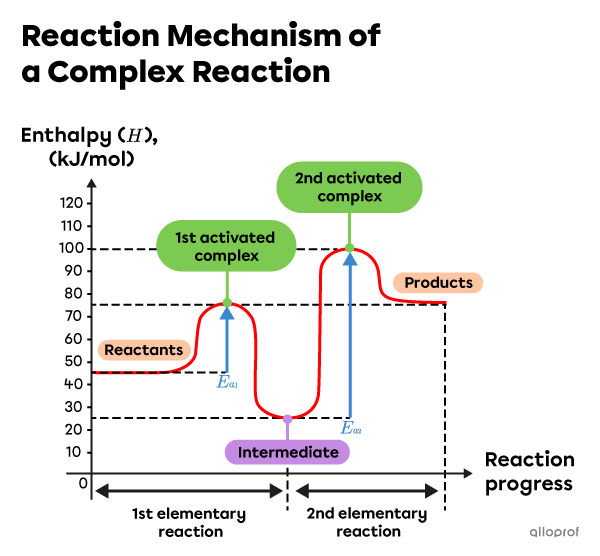
- There are two elementary reactions in this reaction mechanism as indicated by the presence of 2 activated complexes.
- The enthalpy of the reaction intermediate is |25\ \text{kJ}.|
- The activation energy of the first elementary reaction is |30\ \text{kJ}.| It is calculated as follows:
||\begin{align}E_{a_1} &= H_{1st\ activated\ complex} - H_{Reactants}\\
E_{a_1} &= 75\ \text{kJ} - 45\ \text{kJ} \\
E_{a_1} &= 30\ \text{kJ}\end{align}||
The activation energy of the second elementary reaction is |75\ \text{kJ}.| It is calculated as follows:
||\begin{align}E_{a_2} &= H_{2nd\ activated\ complex} - H_{Intermediate}\\
E_{a_2} &= 100\ \text{kJ} - 25\ \text{kJ} \\
E_{a_2} &= 75\ \text{kJ}\end{align}|| - The rate-determining step is the elementary reaction with the highest activation energy. In this reaction mechanism, the second elementary reaction is the determining step: |E_{a_2} = 75\ \text{kJ}.|
The complex reaction between nitrogen dioxide |(\text{NO}_2)| and fluorine |(\text{F}_2)| requires 2 elementary reactions.
Step 1: |\text{NO}_{2\text{(g)}}\ + \text{F}_{2\text{(g)}} \rightarrow\ \text{NO}_2\text{F}_{\text{(g)}} + \text{F}_{\text{(g)}}|
This step progresses slowly.
Step 2: |\text{F}_{\text{(g)}} + \text{NO}_{2\text{(g)}} → \text{NO}_2\text{F}_{\text{(g)}}|
This step progresses quickly.
Overall reaction: |2\ \text{NO}_{2\text{(g)}} + \text{F}_{2\text{(g)}} → 2\ \text{NO}_2\text{F}_{\text{(g)}}|
a) Identify the reaction intermediate.
b) Identify the rate-determining step of this reaction mechanism.
a) The reaction intermediate is the substance that temporarily forms at the end of one elementary reaction and is used up during the next. Here, the intermediate is |\text{F}_{\text{(g)}}.|
b) The rate-determining step is the slowest step of the reaction mechanism. Here, the rate-determining step is Step 1.