To add one polynomial to another, add together the like terms from the first and second polynomial. Then, simplify the algebraic expression obtained. The result is a new polynomial equivalent to the desired sum.
There are three steps to follow when adding polynomials.
-
Group like terms.
-
Add the constant terms.
-
Add the coefficients of the like terms.
Algebraic simplification or algebra tiles can be used to add algebraic expressions.
Note that in the addition:
-
only like terms can be simplified;
-
only the coefficients of each like term are added together.
It is rare for an equation to only have additions. If there are more than one type of operation, make sure to follow the order of operations while simplifying the algebraic expression.
The sum of two polynomials is obtained by adding the like terms of the two polynomials. The sum itself will also be a polynomial.
Consider the following algebraic expression. ||(x^3+x^2+2x+1)+(x^2+xy+3x+y+3)||
The brackets separate the two polynomials that must be added. They can be removed since the addition symbol does not change the signs of the second polynomial’s coefficients.
-
Group the like terms (the same letters, with the same exponents). ||x^3+\color{green}{x^2}+\color{green}{x^2}+xy+\color{red}{2x}+\color{red}{3x}+y+\color{blue}{1+3}||
-
Add the constant terms. ||x^3+\color{green}{x^2}+\color{green}{x^2}+xy+\color{red}{2x}+\color{red}{3x}+y+\color{blue}{1+3}||
-
Add the coefficients of the like terms. ||x^3+\color{green}{2x^2}+xy+\color{red}{5x}+y+\color{blue}{4}||
The result is |x^3+2x^2+xy+5x+y+4.|
Consider the following algebraic expression. ||(2x^3+x^2-2x+2)+(x^3-3x^2+4x-5)||
The brackets separate the two polynomials that must be added. They can be removed since the addition symbol does not change the signs of the second polynomial’s coefficients.
-
Group the like terms (the same letters, with the same exponents). ||\color{green}{2x^3}+\color{green}{x^3}+\color{red}{x^2}+\color{red}{(-3x^2)}+\color{blue}{(-2x)}+\color{blue}{4x}+2-5||
-
Add the constant terms. ||\color{green}{2x^3}+\color{green}{x^3}+\color{red}{x^2}+\color{red}{(-3x^2)}+\color{blue}{(-2x)}+\color{blue}{4x}-3||
-
Add the coefficients of the like terms. ||\color{green}{3x^3}+\color{red}{(-2x^2)}+\color{blue}{2x}-3||
The result is |3x^3-2x^2+2x-3.|
It is possible to check if the initial expression is equivalent to the simplified expression. Substitute a chosen value into each variable and calculate the value of each expression. If the expressions have the same value, they are equivalent.
To check if the second example above is correct (|2x^3+x^2-2x+2+x^3-3x^2+4x-5=3x^3-2x^2+2x-3|), choose a value for the variables. For example, if |x = 2|: ||\begin{align}2(\color{red}{2})^3+\color{red}{2}^2-2(\color{red}{2})+2+\color{red}{2}^3-3(\color{red}{2})^2+4(\color{red}{2})-5&=3(\color{red}{2})^3-2(\color{red}{2})^2+2(\color{red}{2})-3\\ \\
16+4-4+2+8-12+8-5&=24-8+4-3\\ \\
17&=17\end{align}|| Therefore, the two expressions are equivalent.
To help better visualize the addition of polynomials, they can be represented using algebra tiles. To use algebra tiles, first represent each of the algebraic expressions with a group of tiles. Group the identical tiles together and then add them.
Consider the following two polynomials represented by algebra tiles.
|x^3+x^2+2x+1|
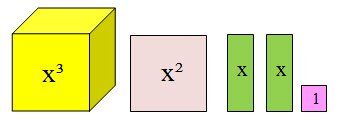
|x^2+xy+3x+y+3|
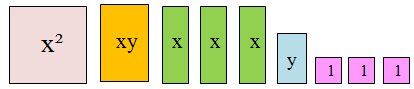
This is what adding these two polynomials looks like using algebra tiles.
|(x^3+x^2+2x+1)+(x^2+xy+3x+y+3)|
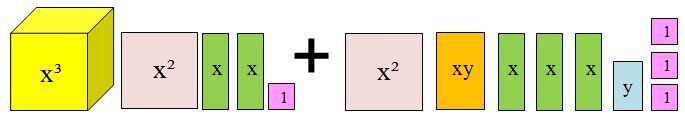
Identical tiles must be grouped together.

Add the tiles.
|x^3+2x^2+xy+5x+y+4|