Algebra is a branch of mathematics that generalizes the rules of arithmetic calculations through the use of variables.
-
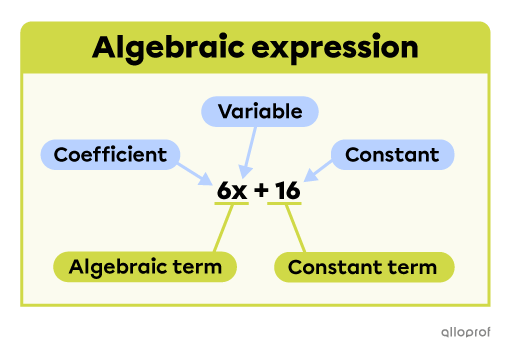
An algebraic expression is a series of algebraic and constant terms linked together by addition |(+)| and subtraction |(-).|
-
A term is an element of an algebraic expression that is composed of a number and/or variables.
-
A variable is a letter that may represent different values.
-
A coefficient is a number that is multiplied by one or more variables.
-
A constant is a number that is not multiplied by a variable.
A term can assume many forms.
| No visible coefficient | Visible coefficient | |
|---|---|---|
| No variable |
|25| |
|
| 1 variable |
|x| |
|5x| |
| Several variables |
|xy| |
|5xy| |
| 1 or more variables with exponents |
|x^2y| |
|5x^2y| |
Algebra has its own writing conventions.
Writing different elements together, one after the other, means that they are multiplied. For instance, |6c| means |6\times c| and |7a^2b| means |7\times a\times a \times b.|
Similarly, when a term has no visible coefficient, its coefficient is 1. In other words, |1b = 1\times b = b| since the number |1| is the neutral element of multiplication.
The same applies to exponents. When a variable has no visible exponent, the exponent is simply 1. So, |5x=5x^1| and |10xy^2=10x^1y^2.|
Furthermore, algebraic expressions can be composed of single or multiple terms.
-
If there is only one term, the algebraic expression is a monomial.
Examples: |x,| |8y,| |-4ab,| |\dfrac{9a^2b}{5},| |5a\times 3b,| |8a \div 3| -
If there are several terms, the algebraic expression is a polynomial.
Examples: |x-y,| |x^3+x^2+x+1,| |25x^2y^4-16,| |15ab + 3c \times 6,| |\dfrac{5a+3b}{2}|
It might appear that the algebraic expression |15ab + 3c \times 6| is composed of 3 terms, but in fact it only has 2. This is because distinct terms must be separated by |+| and |-| symbols. In other words, |3c \times 6| counts as just one term.
Similarly, the expression |8a \div 3| is indeed a monomial. It's best to rewrite this expression using fractional notation as follows:||8a\div 3=\dfrac{8a}{3} =\dfrac{8}{3}a||The coefficient of the monomial is |\dfrac{8}{3}.|
An algebraic expression is used to generalize calculations. It corresponds to a chain of operations in which certain quantities have been replaced by letters called variables.
So, given some quantity that can take on different values and a statement related to this quantity, we can translate the statement into an algebraic expression which depends on the quantity. This is called translating a statement into an algebraic expression.
From the statement “Your brother is |2| years older than you,” the following table of values can be constructed:
| Your age (years) |
Your brother’s age (years) |
|---|---|
| |3| | |3+2=5| |
| |8| | |8+2=10| |
| |12| | |12+2=14| |
| ... | ... |
Note that calculating your brother's age always follows this pattern:||\text{Your age}+2=\text{Your brother's age}||Therefore, if you replace “Your age” with the variable |a,| the algebraic expression representing your brother's age becomes |a+2.| ||a+2=\text{Your brother's age}||The 1st term is composed solely of the variable |a| and the 2nd term is a constant term, because your brother is always 2 years older than you, even if your age varies over the years.
When an algebraic expression is equal to a constant term or another algebraic expression, an equation is obtained.
-
Variable : |x|
-
Constant term: |23|
-
Algebraic expressions: |4x-5| and |2x+7|
-
Equations that express the equality between an algebraic expression and a constant term: |4x-5=23| and |23=2x+7|
-
Equations that express the equality between 2 algebraic expressions: |4x-5=2x+7|
In an algebraic expression, terms are considered to be like terms when they are composed of the same variables and assigned the same exponents.
-
The terms |4x| and |5x| are like terms, since they have the same variable |(x)| and are assigned the same exponent value, |1.|
-
The terms |3r^2s^3| and |6r^2s^3| are like terms, since they use the same variables |(r| and |s)| with the same exponents |(2| for the variable |r| and |3| for the variable |s).|
-
The terms |\dfrac{8}{3}ab| and |\dfrac{7ba}{4}| are like terms, even though the variables are not in the same order. According to the commutativity of multiplication, |a\times b = b\times a.| On the other hand, to respect algebraic writing conventions, the 2nd term should be written like so: |\dfrac{7}{4}ab.|
-
The terms |3xy| and |3xyz| are unlike terms because they do not have the same variables.
-
The terms |12r^2 s^3 t| and |2r^2 s^3 t^2| are unlike terms because the exponent of variable |t| is not the same in both terms.
-
The terms |2a^2b^3c^4| and |3b^2 c^3 a^4| are unlike terms. Although they have the same 3 variables: |a,| |b| and |c,| and the same 3 exponents: |2,| |3| and |4,| the correspondence between the variables and exponents is not the same.
As its name suggests, the value of a variable can vary depending on the situation, and it's this characteristic that must be exploited. A variable is assigned a value depending on the context in which it is used.
Replacing a variable with a number is called substitution.
Therefore, after substituting numbers for variables, an algebraic expression becomes a chain of operations. The only thing left to do is to calculate, while respecting the order of operations.
-
If |x = 2| in the algebraic expression |2x +3,| we replace the variable with this value.||\begin{align} 2\boldsymbol{\color{#3b87cd}x}+3 &=2(\boldsymbol{\color{#3b87cd}2})+3 \\ &= 4+3\\ &= 7 \end{align}||Therefore, when |x = 2,| the value of the algebraic expression is |7.|
-
If |a=-1.5| and |b=10| in the algebraic expression |3a-\dfrac{b}{5}+2,| 2 substitutions must be made. ||\begin{align}3\boldsymbol{\color{#3b87cd}a}-\dfrac{\boldsymbol{\color{#3a9a38}b}}{5}+2 &=3(\boldsymbol{\color{#3b87cd}{-1.5}})-\dfrac{\boldsymbol{\color{#3a9a38}{10}}}{5}+2\\[3pt] &= -4.5-2+2\\[3pt] &=-4.5\end{align}||Therefore, in this case, the value of the algebraic expression is |-4.5.|
-
If |w=5| in the expression |-w^2+w+20,| the |w| must be replaced by |5| wherever |w| appears.||\begin{align}-\boldsymbol{\color{#3b87cd}w}^2 + \boldsymbol{\color{#3b87cd}w}+20 &=-\boldsymbol{\color{#3b87cd}{5}}^2 + \boldsymbol{\color{#3b87cd}{5}}+20\\ &= -25+5+20\\ &=0\end{align}||
When writing an algebraic expression, it's important to respect certain writing conventions.
-
The coefficient of a term is always written in front of the variables. It's important to note, however, that a coefficient of |1| is not written in an expression.
-
If a term has several variables, it is best to place these variables in alphabetical order.
-
In a polynomial, the terms are arranged in descending order of their respective degrees. If 2 terms have the same degree, they are written in alphabetical order.
| Convention | Convention Not Respected | Convention Respected |
|---|---|---|
|
|b15c^2| does not respect the convention since it does not begin with the coefficient. |
Instead, write |
|
|3zx^2y| does not respect the convention, since the variables are not listed in alphabetical order. |
Instead, write |
|
|6+5x^2+4y^3| does not respect the convention since its terms are not in descending order of degree. |
Instead, write |
|
|4b-5a| does not respect the convention, since terms with the same degree are not in alphabetical order. |
Instead, write |