An angle (∠) is formed by two line segments or rays that meet or intersect.
There are different types of angles, such as right, acute, and obtuse angles.
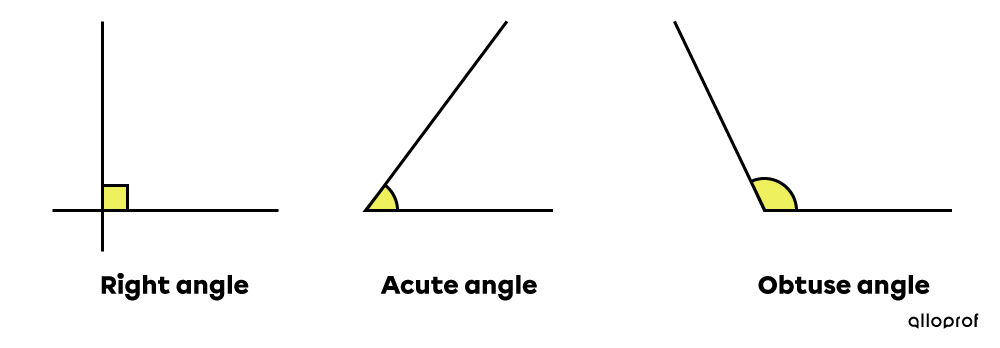
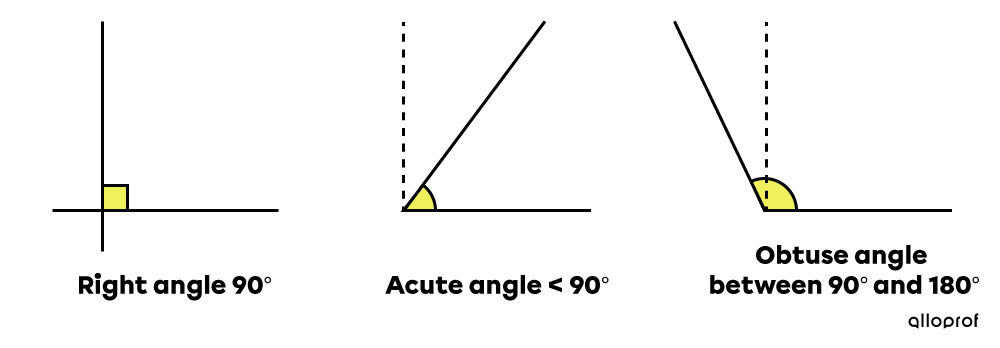
A right angle is an angle formed by two perpendicular rays or line segments.
Examples:
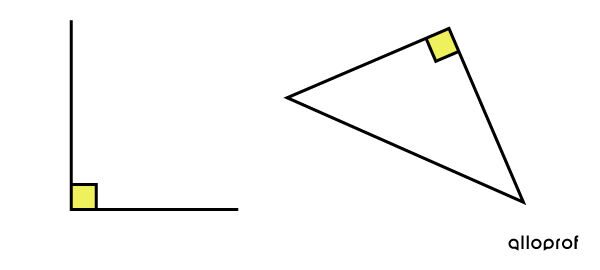
Right angles can be found in many everyday objects.
The corners of frames, doors, and windows form right angles.

To know if an angle is right, place the corner of a sheet of paper on top of it. Compare the line segments or rays that form the angle at the corner of the sheet.
The angle is right when the line segments or rays are aligned with the sides of the sheet.
Example:

An acute angle is an angle smaller than a right angle.
Examples:
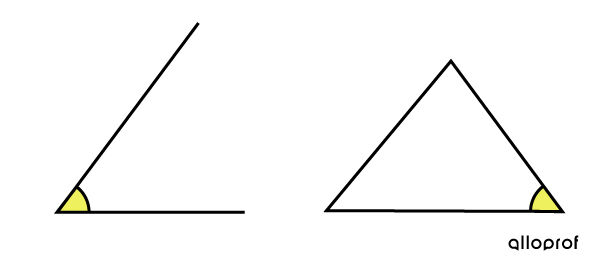
In comparison to a right angle, acute angles are visibly smaller.
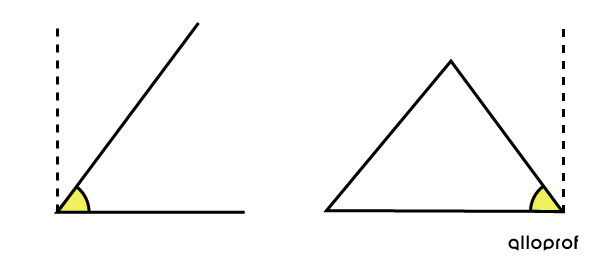
Acute angles can be seen in many everyday objects.
The tips of pencils or carrots and the tops of Christmas trees form acute angles.
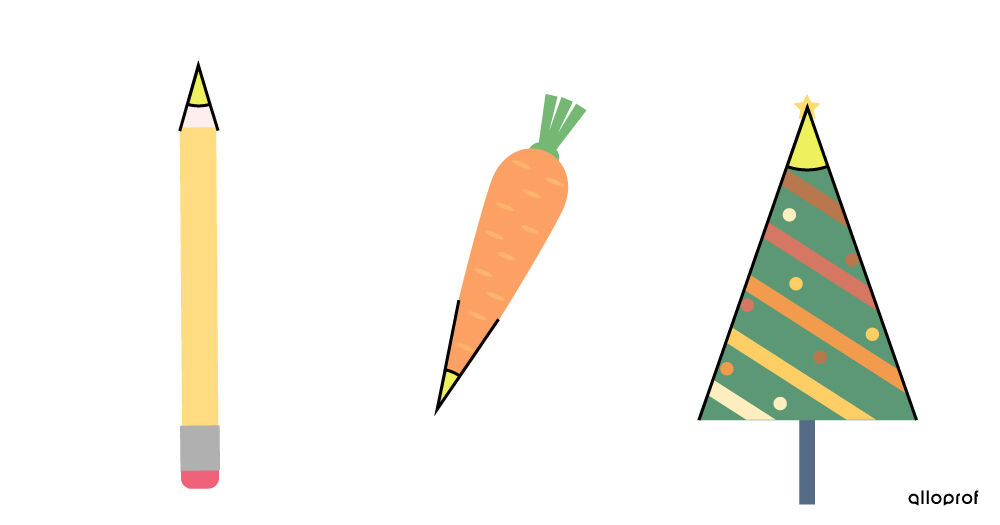
To know if an angle is acute, place the corner of a sheet of paper on top of it. Compare the line segments or rays that form the angle at the corner of the sheet.
The angle is acute when only one line segment or ray of the angle is aligned with one side of the sheet. The other line segment or ray is hidden by the sheet.
Example:

An obtuse angle is an angle greater than a right angle.
Examples:
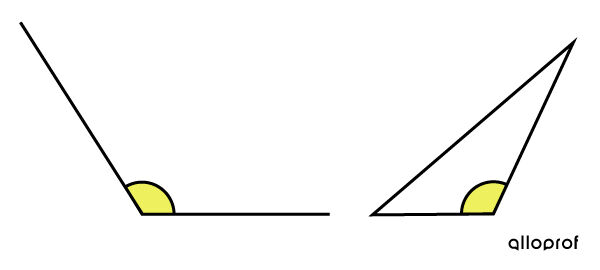
In comparison to a right angle, obtuse angles are visibly larger.
Obtuse angles can be seen in many everyday objects.
The roofs of houses, the backs and seats of lawn chairs, and the corners of stop signs all form obtuse angles.

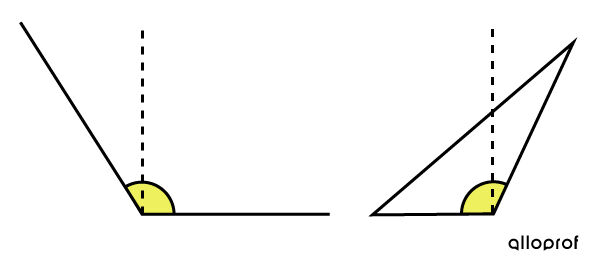
To know if an angle is obtuse, place the corner of a sheet of paper on top of it. Compare the line segments or rays that form the angle at the corner of a sheet.
The angle is obtuse when only one line segment or ray of the angle is aligned with one side of the sheet. The other line segment or ray protrudes from the sheet.
Example:

There are different types of angles, such as right, acute, and obtuse angles.
To learn how to measure angles, see the concept sheet Measuring Angles With a Protractor.
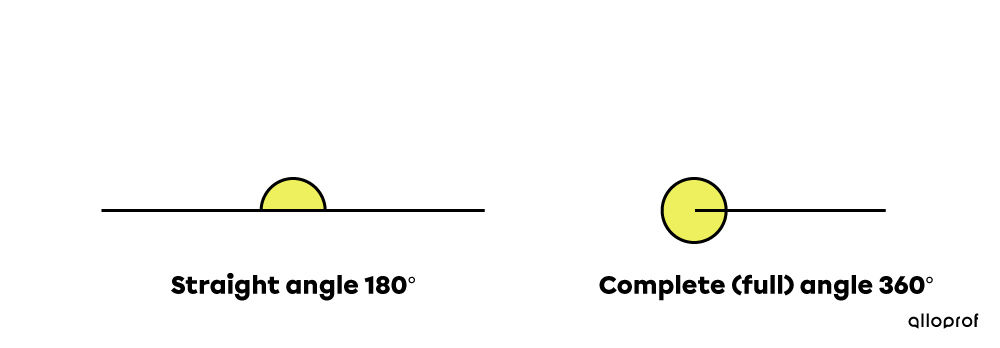
There are also straight angles and complete (full) angles.