In analytical geometry, basic concepts often originate from the points of intersection between lines, figures, and solids. Conics are no exception.
A conic or conical section is a curve obtained when a cone with two nappes is cut with a plane.
A conical surface with two nappes, also called a “double cone”, is created when a line called a generator revolves around an axis.
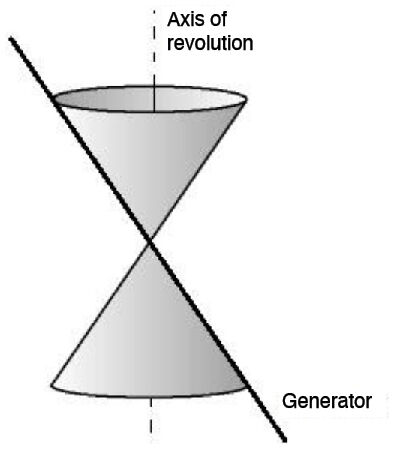
Depending on how the plane intersects the conical surface, we obtain different geometric loci (conics).
Each conic has several characteristics that are important to note. Some are specific to a single type of conic, while other properties are shared by all of them.
The radius of a circle, usually denoted |r,| is the length of the line connecting the centre of the circle to any point on the circle itself.
In the previous diagram, the radius of the circle is represented by the blue line. Notice that if the length of the radius changes, the dimensions of the circle change as well.
An axis of symmetry is an axis that separates any figure into two equal parts.
Circle
As the following animation demonstrates, there are an infinite number of axes of symmetry in a circle.
Ellipse
An ellipse only has 2 axes of symmetry.
Depending on the conic being analyzed, the definition of the vertex can vary.
Ellipse
The vertices of an ellipse are the 4 points located at its extremes.
Hyperbola
The vertices of a hyperbola are the points located at the extremes of each of the branches.
Parabola
The vertex of a parabola is its extreme point.
The Four Vertices of an Ellipse

The Two Vertices of a Hyperbola
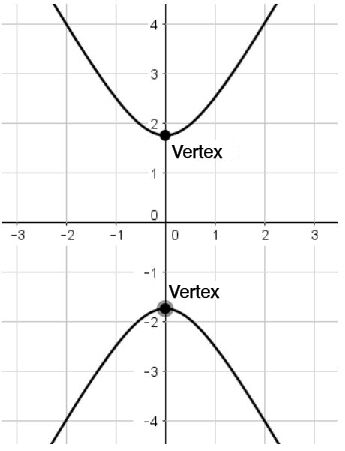
The Vertex of a Parabola
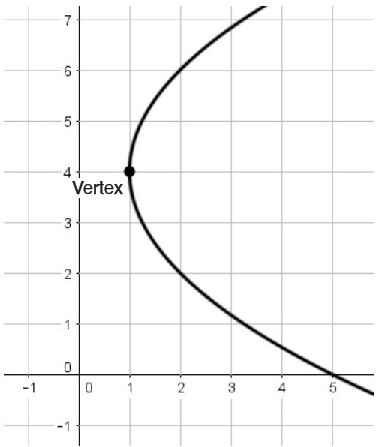
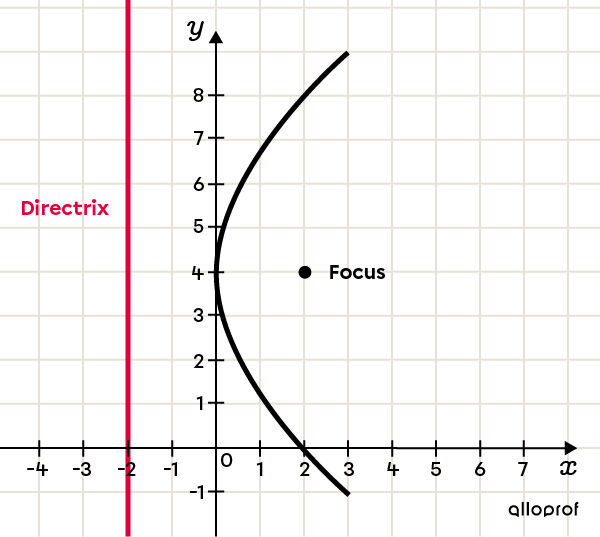
The directrix is a straight line used to define a geometric locus (a set of points satisfying some geometrical condition).
This straight line (coloured red in the graph) allows us to define the parabola, which is in fact the set of points situated at an equal distance from a fixed point (the focus) and from the directrix.
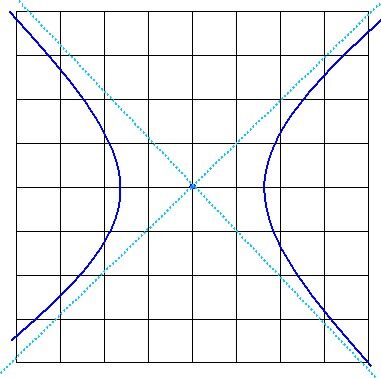
An asymptote is a line that a curve approaches more and more closely without ever reaching it. We would say the distance between a point on the curve and the asymptote tends towards |0|, or approaches |0| (without ever being |0|).
Of the conics considered in this concept sheet, only a hyperbola has asymptotes — 2 of them. In the diagram below, the hyperbola is depicted with a dark blue line, while the asymptotes are drawn in turquoise.
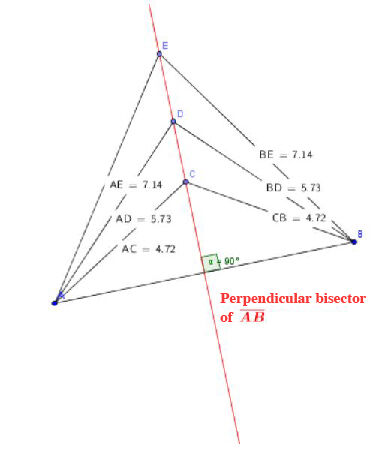
A geometric locus is a set of points in some geometric space that share a common geometric property.
The perpendicular bisector of a line is the locus of all the points located at an equal distance from the two ends of the line.
It is also possible to use curved lines and two — or three — dimensional planes to create different geometric loci. Conics are a good example of geometric loci.