En géométrie analytique, les concepts de base sont souvent créés à partir des points de rencontre entre des segments, des figures et des solides. Le cas des coniques ne fait pas exception.
Une section conique ou conique est une courbe que l'on obtient en coupant une surface conique à deux nappes par un plan.
La surface conique à deux nappes est créée par la révolution d'une génératrice autour d'un axe.
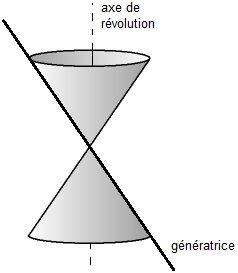
Selon la position du plan qui coupe une surface conique, on obtient un lieu géométrique différent.
Les différentes coniques présentent une multitude de caractéristiques qu'il est important de connaitre. Certaines sont particulières à une seule conique alors que d'autres sont communes à toutes.
Le rayon d'un cercle, généralement noté |r,| est le segment de droite reliant le centre du cercle à n'importe quel point sur le cercle lui-même.
Sur le schéma précédent, le rayon du cercle est représenté par le segment de droite bleu. On remarque également que si la longueur du rayon change, la dimension du cercle est affectée.
L'axe de symétrie est un axe qui sépare la figure en deux portions égales.
Cercle
Comme le démontre l'animation suivante, il existe une infinité d'axes de symétrie dans un cercle.
Ellipse
L'ellipse ne compte que 2 axes de symétrie.
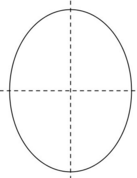
Tout dépendant de la conique qu'on analyse, la définition du sommet peut varier.
Ellipse
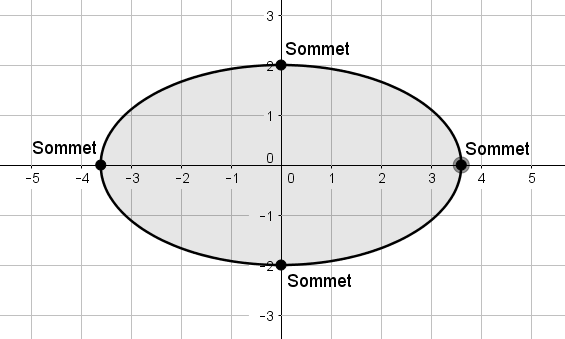
Les sommets d'une ellipse sont les 4 points situés à ses extrémités.
Hyperbole
Les sommets d'une hyperbole sont les points situés à l'extrémité de chacune des branches.
Parabole
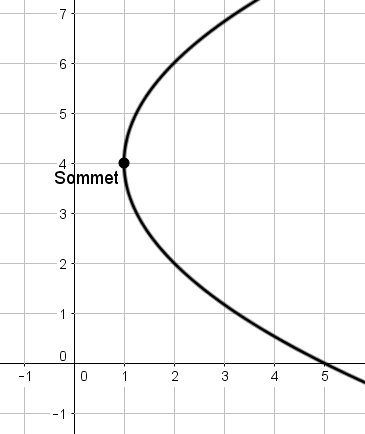
Le sommet d'une parabole est le point situé à son extrémité.
Les quatre sommets d'une ellipse
Les deux sommets d'une hyperbole
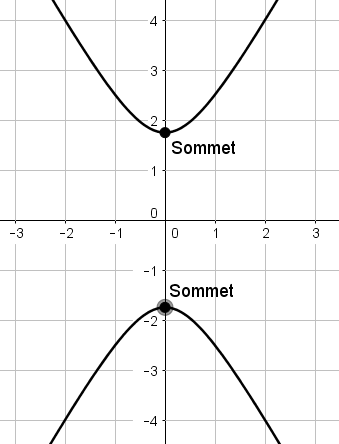
Le sommet d'une parabole
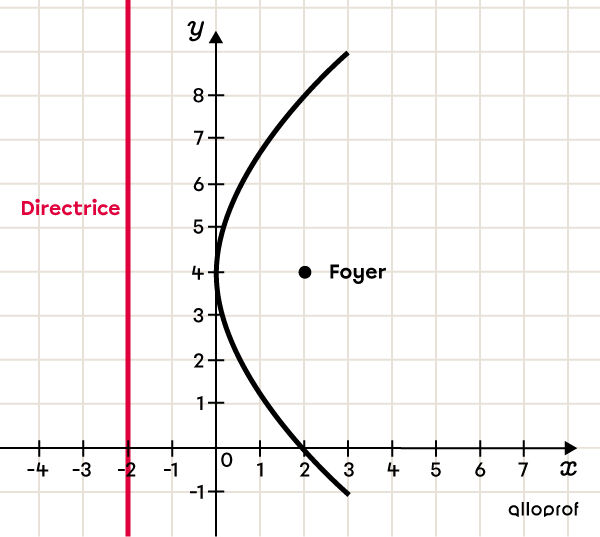
Le foyer est un point qui sert à définir une conique.
On utilise habituellement le concept de foyer lorsqu'on caractérise les coniques suivantes :
La directrice est une droite servant à définir un lieu géométrique.
Cette droite (en rouge sur la figure) permet de définir la parabole, qui est en fait le lieu des points situés à la même distance d'un point fixe (le foyer) et de la directrice.
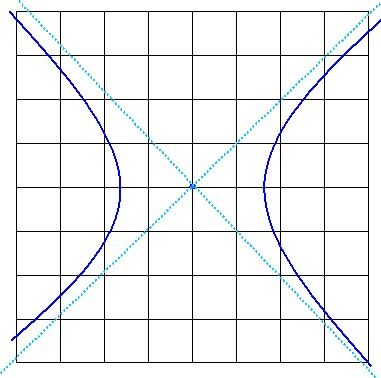
Une asymptote est une droite vers laquelle une courbe s'approche de plus en plus sans toutefois l'atteindre. On dit alors que la distance entre un point sur la courbe et l'asymptote tend vers 0 (sans jamais être 0).
Parmi les coniques étudiées dans cette fiche, seule l'hyperbole possède des asymptotes, qui sont au nombre de deux. Sur le schéma ci-dessous, l'hyperbole est représentée par la ligne bleu foncé alors que les asymptotes sont tracées en turquoise.
Un lieu géométrique est un ensemble de points d'un espace géométrique qui sont caractérisés par une propriété métrique commune.
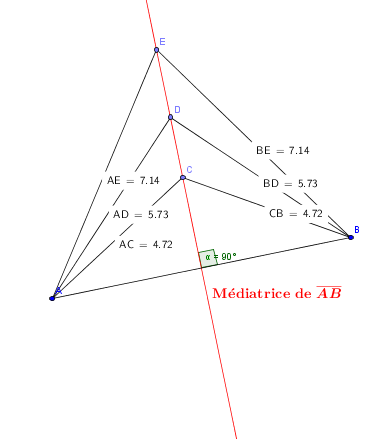
La médiatrice d'un segment est le lieu géométrique de tous les points qui sont situés à égale distance des deux extrémités de ce segment.
Il est également possible de travailler avec des lignes courbes et des plans à deux ou trois dimensions afin de créer différents lieux géométriques. Les coniques sont de bons exemples de lieux géométriques.