Constructing a trapezoid requires the use of geometry tools such as a ruler, set square, protractor, and/or compass. Furthermore, it is important to note the differences between standard, isosceles, and right trapezoids.
A trapezoid is a quadrilateral that has one pair of parallel sides named "small base" and "large base" due to their different lengths.
Considering the definition, a trapezoid can be constructed by simply drawing two parallel lines of different lengths to then form the quadrilateral, without taking into account the measurement of the other sides or angles. On the other hand, a trapezoid’s height measurement can also be important.
A trapezoid can be drawn using a ruler and a set square when the measurement of the bases and height are known. Follow these steps:
-
Using a ruler, draw a line segment that corresponds to the length of the large base.
-
Place the set square anywhere on the large base and draw a perpendicular line segment longer than the trapezoid’s height.
-
Using the ruler, mark the spot on the perpendicular line that corresponds to the trapezoid’s height.
-
Place the set square on that mark and draw a line that extends from it.
-
Use the ruler to make sure the line drawn in step 4 is the length of the small base.
-
Using the ruler, connect the ends of each base.
Consider on the following example:
Draw a trapezoid with a large base of |7\:\text{cm}|, a small base of |4\:\text{cm}| and a height of |3\:\text{cm}|.
|
|
|
|
|
|
A trapezoid can be constructed using a protractor and a ruler when the measurements of the sides and the value of at least two angles are known.
-
Using a ruler, draw a line segment that corresponds to the length of the large base.
-
Place the protractor at one end of the large base and draw an angle according to the specified measurement.
-
Using the ruler, extend the angle line so that it is the same length as the trapezoid’s oblique side.
-
Repeat steps 2 and 3 on the other end of the large base, making sure the angle and oblique line correspond to the specified measurements.
-
Using the ruler, connect the ends of the two oblique line segments.
Using the measurements given below, follow these steps to build the trapezoid.
Draw a trapezoid with bases measuring |5\:\text{cm}| and |2.5\:\text{cm}|, as well as oblique sides measuring |2.5\:\text{cm}| and |3\:\text{cm}|. Finally, the measurements of the acute angles formed by the oblique sides and the large base are |70^o| and |51^o|, respectively.
|
|
|
|
|
|
An isosceles trapezoid is a quadrilateral with a pair of congruent sides. It also has another pair of parallel opposite sides named the "small base" and "large base" due to their different lengths.
An isosceles trapezoid can be constructed using a ruler and a set square when the measurement of the bases and the height are known. Here is a step-by-step guide:
-
Using a ruler, draw a line segment that corresponds to the length of the large base.
-
Place the set square on one end of the large base and draw a perpendicular line segment longer than the trapezoid’s height.
-
Using the ruler, mark the spot on the perpendicular line that corresponds to the trapezoid’s height.
-
Repeat steps 2 and 3 on the other end of the large base.
-
Using the ruler, join the two marks that represent the trapezoid’s height.
-
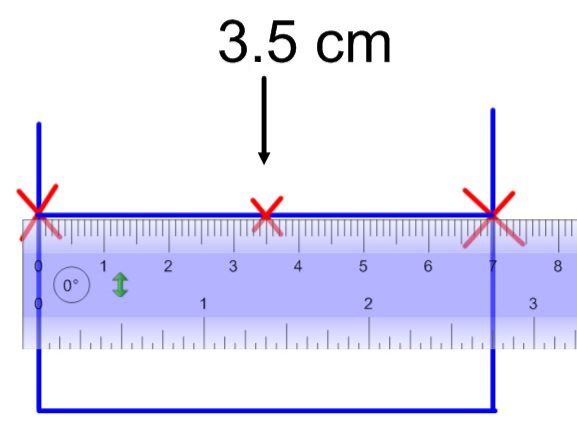
Using the ruler, locate and mark the midpoint of the line segment drawn in step 5.
-
Using the ruler, measure half the length of the small base. Mark this distance on either side of the midpoint found in step 6
-
Join the ends of the large base to the marks made in step 7.
Consider the following example.
Draw an isosceles trapezoid with a large base measuring |7\:\text{cm}|, a small base measuring |4\:\text{cm}|, and a height equal to |3\:\text{cm}|.
|
|
|
|
|
 |
|
|
An isosceles trapezoid can be constructed using a protractor and ruler when the measurements of the sides and the value of at least two angles are known. Follow these steps:
-
Using a ruler, draw a line segment that corresponds to the length of the large base.
-
Place the protractor at one end of the large base and draw the angle according to the specified measurement.
-
Using the ruler, extend the angle’s line to equal the length of the trapezoid’s oblique side.
-
Repeat steps 2 and 3 on the other end of the large base.
-
Using the ruler, connect the endpoints of the two oblique segments.
Follow these steps to construct an isosceles trapezoid with these given measurements.
Draw an isosceles trapezoid with a large base measuring |10\:\text{cm}|, oblique sides measuring |4\:\text{cm}|, and acute angles measuring |45^o|.
|
|
|
|
|
|
A right trapezoid has two consecutive right angles and a pair of opposing parallel sides named the "small base" and "large base" because of their different lengths.
A right trapezoid can be constructed using a ruler and set square when the measurement of the bases and the height are known.
-
Using a ruler, draw a line segment that corresponds to the length of the large base.
-
Place the set square at one end of the large base and draw a perpendicular line segment longer than the trapezoid’s height.
-
Using the ruler, mark the spot on the perpendicular line segment that corresponds to the trapezoid’s height.
-
Place the set square on the height of the trapezoid where the line of the small base will go.
-
Use the ruler to draw the line that is the length of the small base (4 cm).
-
Using the ruler, join the ends of each base.
Consider the following example:
Draw a rectangle trapezoid with the large base measuring |7\:\text{cm}|, the small base measuring |4\:\text{cm}|, and a height equal to |3\:\text{cm}|.
|
|
|
|
|
|
A right trapezoid can be constructed using a protractor and ruler when the measurements of the bases and the height are known.
-
Using a ruler, draw a line segment that corresponds to the length of the large.
-
Place the protractor at one end of the large base and draw the 90o angle.
-
Using the ruler, extend the angle’s line so that it is the length of the trapezoid’s height.
-
Repeat steps 2 and 3 on the other end of the height.
-
Using the ruler, join the endpoints of the two bases.
With the given measurements, follow these steps to construct a right trapezoid.
Draw a right trapezoid with bases measuring |6\:\text{cm}| and |4\:\text{cm}| and the height measuring |3\:\text{cm}|.
|
|
|
|
|
|