Quadrilaterals are closed polygons with 4 sides.
There are several classes of quadrilaterals. To classify them, analyze the measurements of the sides, the measurements of the angles, and the relative position of the sides.
Below is a diagram that illustrates the relationships between families of quadrilaterals.
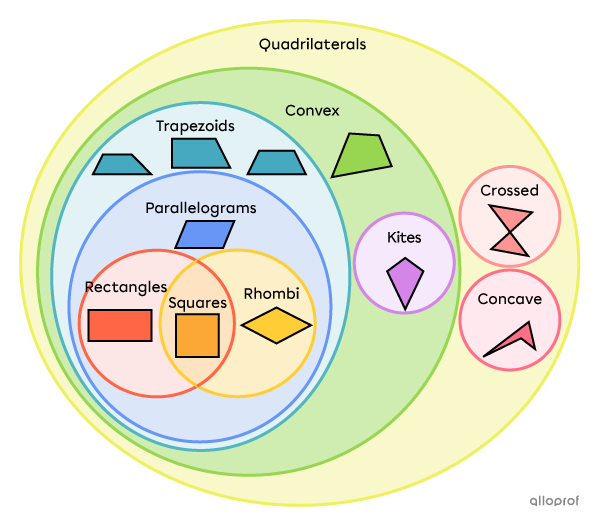
In the diagram we can distinguish between the 3 main classes of quadrilaterals: crossed, convex, and non-convex (or concave).
The convex quadrilaterals at the centre of the diagram have special characteristics.
A convex quadrilateral is a trapezoid if it has at least 1 pair of parallel sides.
A trapezoid with 2 pairs of parallel sides is a parallelogram.
A parallelogram with 4 congruent sides is a rhombus, while a parallelogram with 4 right angles is a rectangle.
Finally, a square is both a rectangle and a rhombus (with 4 congruent sides and 4 right angles).
The image below is a decision tree that helps classify quadrilaterals based upon their properties.

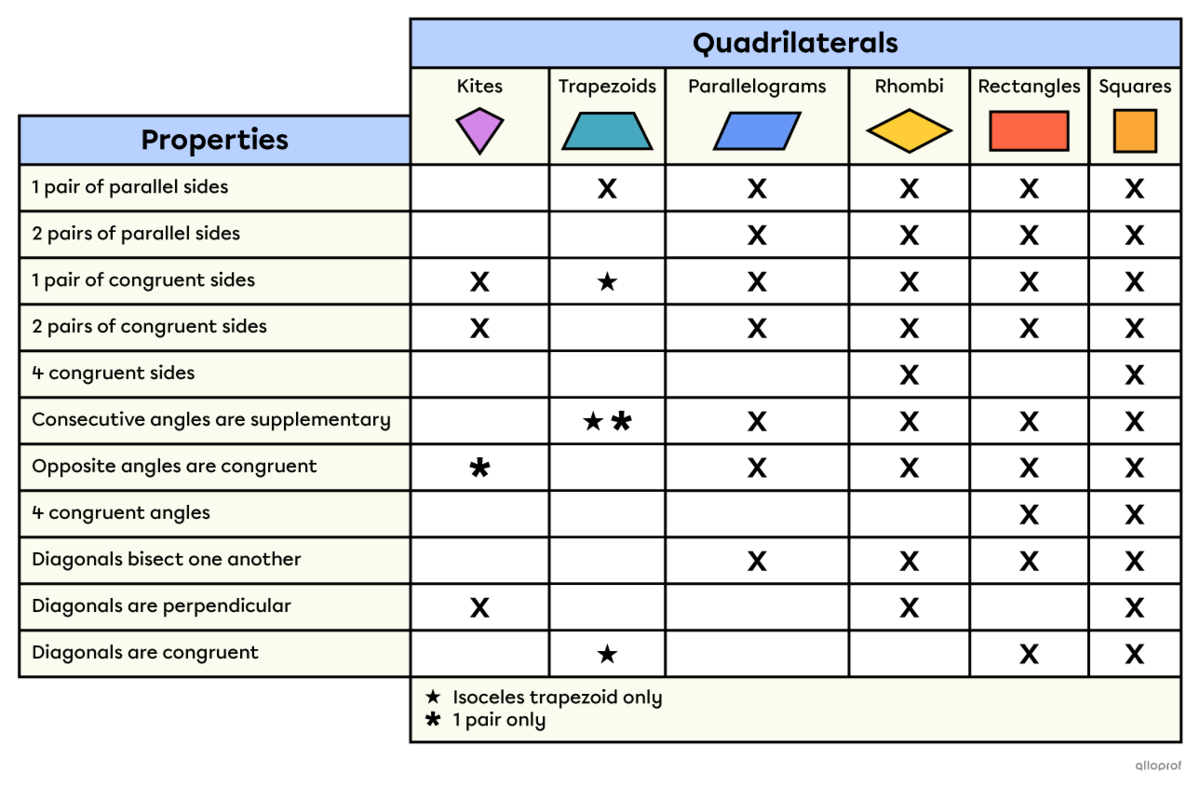
Below is a table that summarizes the various properties of quadrilaterals.
A kite is a convex quadrilateral with 2 pairs of adjacent congruent sides.
The kite has the following properties:
-
1 pair of opposite, congruent angles
-
diagonals that are perpendicular.
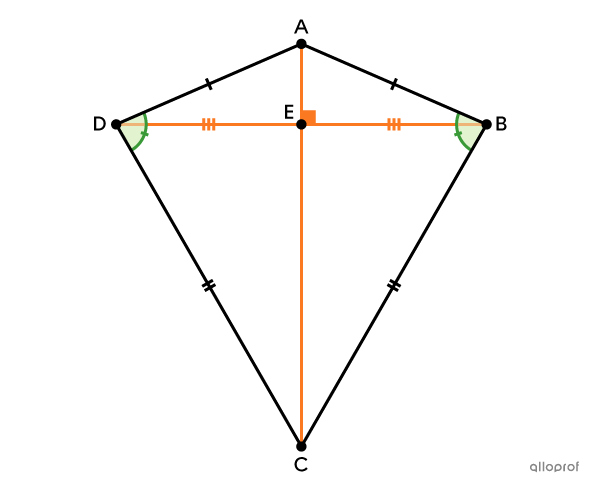
Definition
It has 2 pairs of adjacent congruent sides.||\begin{align}\overline{AB} &\cong \overline{AD}\\\overline{BC} &\cong \overline{CD}\end{align}||
Properties
It has 1 pair of opposite, congruent angles.||\angle{ABC}\cong\angle{ADC}||
Its diagonals are perpendicular.||\overline{AC}\perp\overline{BD}||
A trapezoid is a convex quadrilateral with at least 1 pair of parallel sides.
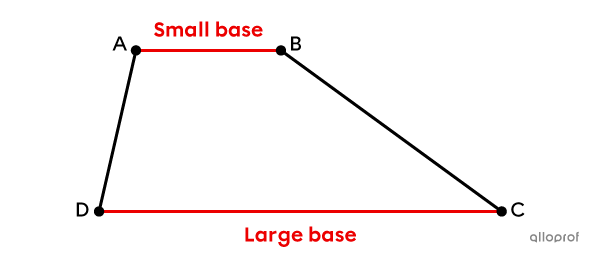
Definition
It has at least 1 pair of parallel sides.||\overline{AB} \parallel \overline{CD}||
A right trapezoid is a trapezoid with at least 2 right angles.
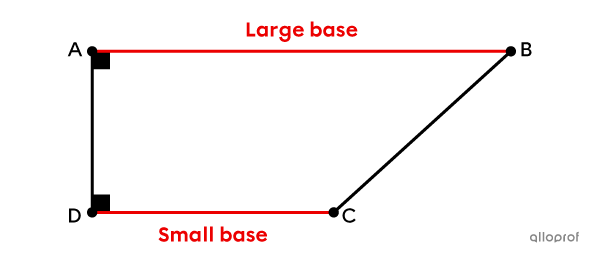
Definition
It has at least 1 pair of parallel sides.||\overline{AB} \parallel \overline{CD}||
It has 2 right angles.||\begin{align}\text{m}\angle{DAB}&=90^\circ\\ \text{m}\angle{ADC}&=90^\circ\end{align}||
An isosceles trapezoid is a trapezoid with non-parallel sides that are congruent.
The isosceles trapezoid has the following properties:
-
2 pairs of adjacent supplementary angles
-
2 pairs of adjacent congruent angles
-
diagonals that are congruent.
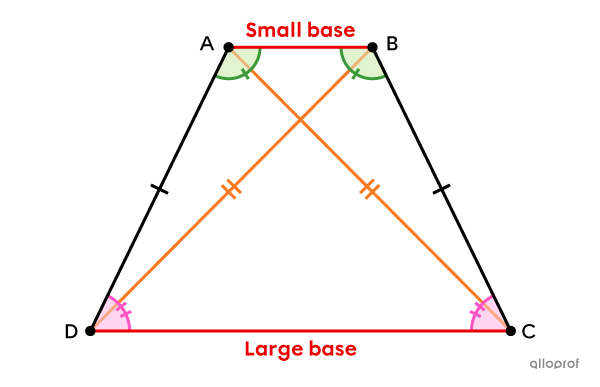
Definition
It has at least 1 pair of parallel sides.||\overline{AB} \parallel \overline{CD}||
Its non-parallel sides are congruent.||\overline{AD}\ \cong\ \overline{BC}||
Properties
It has 2 pairs of adjacent supplementary angles.||\begin{align}\text{m}\angle{BAD}+\text{m}\angle{ADC}&=180^\circ\\ \text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\end{align}||
It has 2 pairs of adjacent congruent angles.||\begin{align}\angle{BAD}&\cong\angle{ABC}\\ \angle{ADC}&\cong\angle{BCD}\end{align}||
Its diagonals are congruent.||\overline{AC}\cong\overline{BD}||
A parallelogram is a convex quadrilateral with 2 pairs of opposite sides that are parallel.
The parallelogram has the following properties:
-
opposite angles that are congruent
-
2 pairs of adjacent supplementary angles
-
opposite sides that are congruent
-
diagonals that bisect each other.
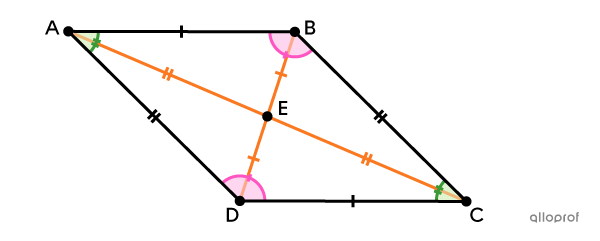
Definition
It has 2 pairs of opposite sides that are parallel.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
Properties
Its opposite angles are congruent.||\begin{align}\angle{ABC}&\cong\angle{ADC}\\ \angle{DAB}&\cong\angle{BCD}\end{align}||
It has 2 pairs of adjacent supplementary angles.||\begin{align}\text{m}\angle{BAD}+\text{m}\angle{ADC}&=180^\circ\\\text{m}\angle{BAD}+\text{m}\angle{ABC}&=180^\circ\\ \text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\\\text{m}\angle{ADC}+\text{m}\angle{BCD}&=180^\circ\end{align}||
Its opposite sides are congruent.||\begin{align}\overline{AB} &\cong \overline{CD}\\\overline{AD} &\cong \overline{BC}\end{align}||
Its diagonals bisect one another.||\begin{align}\overline{BE}&\cong \overline{DE}\\ \overline{AE}&\cong \overline{CE}\end{align}||
A rhombus is a convex quadrilateral with 4 congruent sides.
The rhombus has the following properties:
-
opposite angles that are congruent
-
adjacent angles that are supplementary
-
opposite sides that are parallel
-
diagonals that bisect one another and are perpendicular.
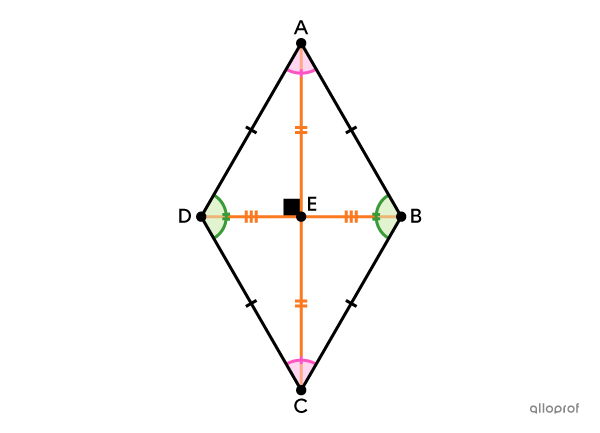
Definition
It has 4 congruent sides.||\overline{AB}\cong \overline{BC}\cong \overline{CD}\cong \overline{AD}||
Properties
Its opposite angles are congruent.||\begin{align}\angle{ABC}&\cong\angle{ADC}\\ \angle{DAB}&\cong\angle{DCB}\end{align}||
Its adjacent angles are supplementary.||\begin{align}\text{m}\angle{DAB}+\text{m}\angle{ABC}&=180^\circ\\
\text{m}\angle{ABC}+\text{m}\angle{BCD}&=180^\circ\\
\text{m}\angle{BCD}+\text{m}\angle{CDA}&=180^\circ\\
\text{m}\angle{CDA}+\text{m}\angle{DAB}&=180^\circ\end{align}||
Its opposite sides are parallel.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel\overline{BC}\end{align}||
Its diagonals bisect one another.||\begin{align}\overline{DE}&\cong \overline{BE}\\ \overline{AE}&\cong \overline{CE}\end{align}||
Its diagonals are perpendicular.||\overline{AC}\perp\overline{BD}||
A rectangle is a convex quadrilateral with 4 right angles.
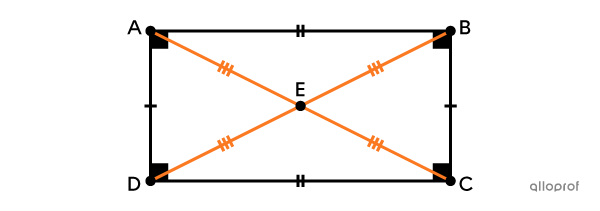
Definition
It has 4 angles that measure |90^\circ.|||\text{m}\angle{ABC}=\text{m}\angle{BCD}=\text{m}\angle{CDA}=\text{m}\angle{DAB}=90^\circ||
Properties
It has 2 pairs of opposite sides that are parallel.||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
It has 2 pairs of opposite sides that are congruent.||\begin{align}\overline{AB} &\cong \overline{CD}\\\overline{AD} &\cong \overline{BC}\end{align}||
Its diagonals are congruent.||\overline{AC}\cong\overline{DB}||
Its diagonals bisect each other.||\begin{align}\overline{AE}&\cong \overline{CE}\\ \overline{DE}&\cong \overline{BE}\end{align}||
A square is a quadrilateral with 4 right angles and 4 congruent sides.
The rectangle has the following properties:
-
opposite sides that are parallel
-
diagonals that are perpendicular, bisect each other, and are congruent.
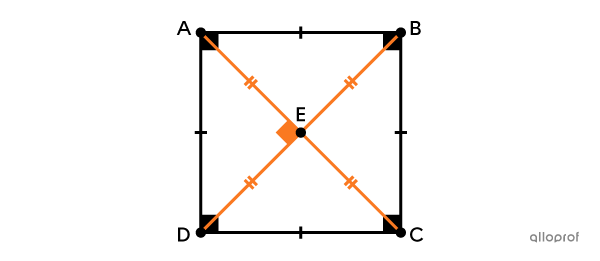
Definition
It has 4 right angles.||\text{m}\angle{ABC}=\text{m}\angle{BCD}=\text{m}\angle{CDA}=\text{m}\angle{DAB}=90^\circ||
It has 4 congruent sides.||\overline{AB} \cong \overline{BC}\cong \overline{CD} \cong \overline{AD}||
Properties
It has 2 pairs of parallel sides. ||\begin{align}\overline{AB} &\parallel \overline{CD}\\\overline{AD} &\parallel \overline{BC}\end{align}||
Its diagonals are perpendicular.||\overline{AC}\perp\overline{BD}||
Its diagonals bisect each other.||\begin{align}\overline{AE}&\cong \overline{CE}\\ \overline{BE}&\cong \overline{DE}\end{align}||
Its diagonals are congruent.||\overline{AC}\cong\overline{BD}||
