Since polyhedrons are a subcategory of solids, they have their own characteristics. More precisely, it is possible to define polyhedrons according to edges, vertices, and faces. In addition, it is possible to relate each of the concepts.
More precisely, this mathematical formula makes it possible to associate the number of edges, faces, and vertices of a polyhedron. It is named after the mathematician who created it: Leonhard Euler.
The formula applies only to polyhedrons and not curved solids (e.g., cylinder, cone, sphere, etc.) Their curved surfaces ensure that they are not affected by Euler's Theorem.
Since the formula is based on the quantitative character of vertices, edges, and faces, it can be summarized with the following formula:
||V + F - 2 = E||
where
|\begin{align} V &= \text{Number of vertices}\\
F &= \text{Number of faces}\\
E &= \text{Number of edges}\end{align}|
To determine each of the quantities, count them by analyzing the given polyhedron.
Use Euler's Formula to calculate the number of edges of the following right pentagonal pyramid.
According to Euler's Theorem: ||\begin{align} \color{blue}{V} + \color{red}{F} - 2 &= E\\
\color{blue}{6} + \color{red}{6} - 2 &= A\\
10 &= A\end{align}||
The pyramid has 10 edges.
Despite its simplistic appearance, the formula can be written in several different ways by applying some algebraic manipulations.
||\begin{align} V + F - 2 &= E \\
V + F &= E + 2\end{align}||
In this case, it is simply the |2| that changes sides in the equality.
||\begin{align} V + F - 2 &= E\\
V + F - 2 \color{red}{+ 2} &= E \color{red}{+ 2}\\
V + F &= E + 2\end{align}||
Even if the formula is only true for polyhedrons, there are several types of polyhedrons to consider. The formula can be used for both convex polyhedrons and non-convex polyhedrons.
Convex Polyhedrons
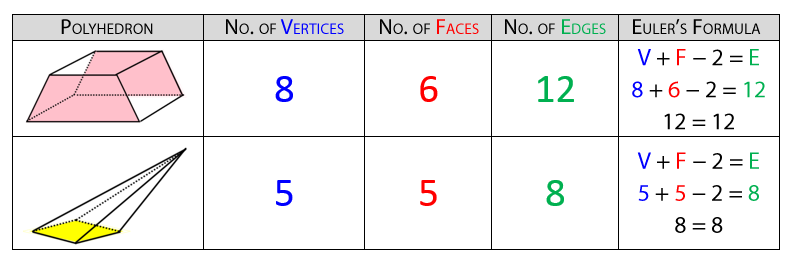
Non-Convex Polyhedrons
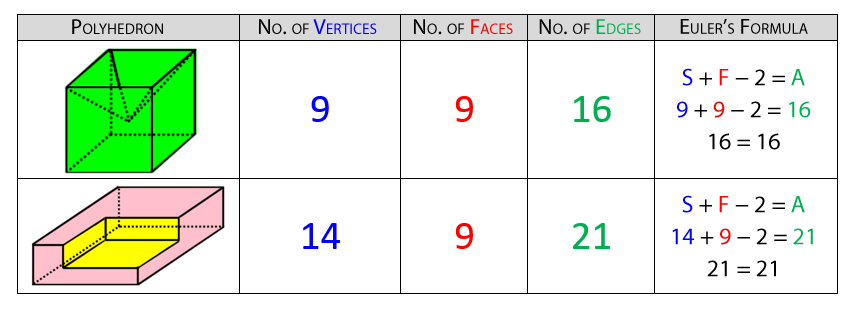
As soon as we have two of the three quantities present in Euler's Formula, the missing quantity can be determined using some arithmetic operations.
Determine the number of vertices of a prism with 6 faces and 12 edges.
-
Determine if Euler's Theorem can be applied
Since it refers to a prism and all prisms are polyhedrons, then Euler’s Formula can be used. -
Apply the formula
Using the information given, the variables are replaced by their respective values.
||\begin{align} V + F - 2 &= E\\
V + 6 - 2 &= 12\\
V + 4 &= 12\end{align}|| -
Find the missing value
According to the last equation, we are looking for a number which, added to 4, will give a total of 12. If we posit that |\color{green}{V = 8}| , the following equality is obtained:
||\begin{align}\color{green}{V} + 4 &= 12\\
\color{green}{8} + 4 &= 12\\
12 &= 12\end{align}|| -
Interpret the answer
This prism contains |\color{green}{8}| vertices.
To find the number of faces according to the number of edges and the number of vertices, use the same steps as presented above.