Euler's theorem was discovered in the 18th century by the mathematician Leonhard Euler. It is a formula that helps calculate the relationships between the number of faces, vertices, and edges of a convex polyhedron. The missing term can be found when two of the three terms present in Euler's formula are known.
To learn more about faces, vertices, and edges, read the concept sheet Faces, Edges, and Vertices.
Here are three formulas that allow you to apply Euler’s theorem. The results are the same when you use any of these formulas.

To determine the number of edges of a convex polyhedron using the formula |F + V - 2 = E,| I have to follow these steps.
How many edges does a convex polyhedron with |8| faces and |12| vertices have?
|
 |
|
 |
|
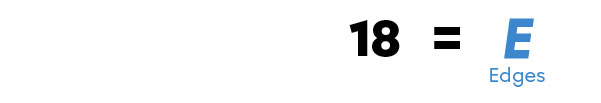 |
A convex polyhedron with |8| faces and |12| vertices has |18| edges.
To determine the number of edges of a convex polyhedron using the formula |F + V - E = 2,| I have to follow these steps.
How many edges does a convex polyhedron with |7| faces and |10| vertices have?
|
 |
|
 |
|
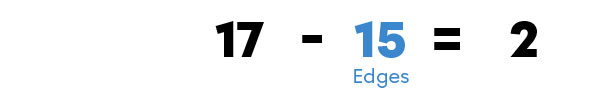 |
A convex polyhedron with |7| faces and |10| vertices has |15| edges.
To determine the number of edges of a convex polyhedron using the formula |F + V = E + 2,| I have to follow these steps.
How many edges does a convex polyhedron with |10| faces and |16| vertices have?
|
 |
|
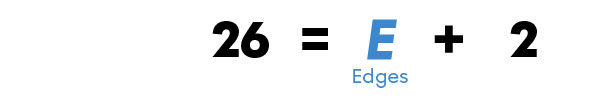 |
|
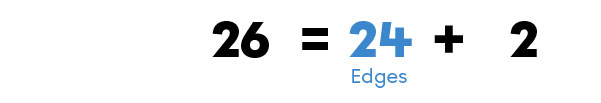 |
A convex polyhedron with |10| faces and |16| vertices has |24| edges.
Using this formula, you can also find the number of faces and vertices of a polyhedron.
To find the number of faces, you need to know the number of vertices and edges.
Example:
How many faces does a polyhedron with |6| vertices and |9| edges have?

To find the number of vertices, you need to know the number of faces and edges.
Example:
How many vertices does a polyhedron with |5| faces and |9| edges have?
