Many fabrics and materials have repeated images or patterns with a pre-established order. Mathematicians refer to these as frieze patterns (friezes) and/or tessellations.
Geometric transformations are needed to produce a frieze pattern and/or tessellation.
In general, a frieze pattern is a repeating pattern that follows a particular order.
A frieze is a continuous strip with parallel edges, formed by repeating one or more patterns. The patterns repeat regularly and harmoniously.
To create the strip, successive reflections, translations or rotations of |180^\circ| are used.
Frieze pattern obtained by translation
In a frieze pattern produced by translation, the ensuing patterns are identical to the initial pattern. They have the same orientation, color arrangement, size, etc.
Frieze pattern obtained by reflection
In a frieze pattern produced by reflection, each pattern is a reflection of one preceding it. Thus, the dimensions are preserved, but the pattern’s orientation changes.
Frieze pattern obtained by rotating |180^\circ|
In a frieze pattern produced by rotation, each ensuing pattern is the result of a rotation of the pattern preceding it. A difference is seen from the reflection when the frieze pattern produced by this rotation is analyzed.
It gets easier to create new frieze patterns when these definitions and examples are kept in mind.
As in many mathematical concepts, we can establish a sequential order that enables the frieze pattern to be properly constructed.
-
Trace the basic pattern
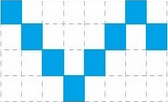
-
Draw the frieze pattern’s axis of reflection
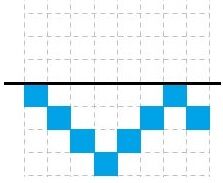
-
Perform the reflection for the pattern’s first section
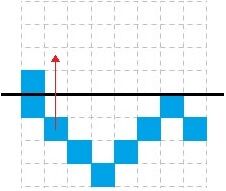
-
Perform a reflection on the rest of the pattern
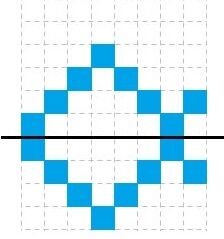
If using reflection seems complicated, we can use translation for an equally interesting result.
Use the same approach as presented above.
-
Trace the basic pattern

-
Draw the frieze pattern’s translation arrow
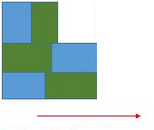
-
Perform the first translation of the basic pattern
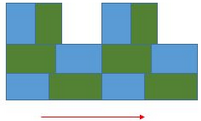
Repeat the translation as often as desired

Regardless of the colours and basic patterns used, simply follow the steps to build a frieze pattern worthy of its name.
For this construction, the rotation is always based on the preceding pattern and not necessarily from the initial pattern image.
-
Trace the basic pattern

-
Identify the centre of rotation
-
Perform the first rotation
-
Repeat the rotation as often as desired
Other than for decorative purposes such as producing frieze patterns for tapestries, the same approach can be used to completely cover different surfaces.
It is equally important to take into account both the basic pattern and space it occupies.
A tessellation is a surface that is completely covered in patterns. It has no empty spaces and no overlap.
Once again, a translation or reflection can be used to produce a tessellation.
A tessellation can be obtained by reflecting one or several patterns.
-
Trace the basic pattern
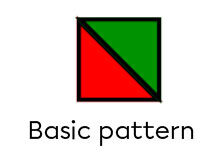
-
Draw a line of reflection
-
Perform the first reflection
-
Reflect as often as desired
It's important to note that lines of reflection can be drawn anywhere. The entire surface must be covered without leaving any empty spaces between patterns.
It's possible to use the same procedure to produce a tessellation by translation as when using a reflection. It's important to always make sure there are no empty spaces between the patterns.
-
Trace the basic pattern
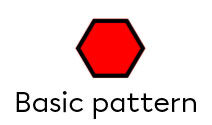
-
Draw the translation arrow
-
Sketch the result of the first translation
-
Repeat the translations as often as desired
It's important to note that the orientation, direction, and length of the translation arrow will vary depending on the image desired. There can be no free space between any of the patterns. The surface must be completely covered.