An image can be modified according to our needs. Thus, we can perform an enlargement or reduction of an image (dilation), a reflection, a rotation, or even a translation of a figure to modify its dimensions or orientation.
Despite the marked differences between each transformation, it is possible to perform more than one geometric transformation within the same context.
In mathematical language, an image obtained after at least one of these modifications has experienced a geometric transformation.
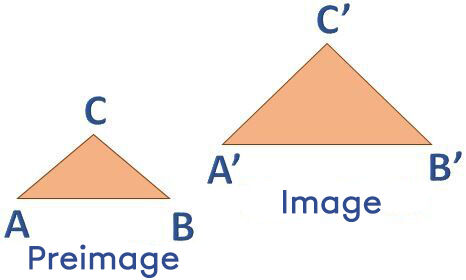
A geometric transformation involves moving an initial figure (preimage) or changing its dimensions to produce a new figure called the image.
To differentiate the preimage from the image, use a different notation set to identify the vertices.
It is important to identify the vertices of the preimage and the image with capital letters. The same letters are used for the corresponding vertices in both figures, which are located in the same place in each figure. The letter in the image must contain an apostrophe, called "prime".
Finally, each geometric transformation has very specific properties; however, there is one property associated with almost all transformations.
A geometric transformation is said to be isometric when the image keeps the same interior angle measurements (corresponding angles) and the same side measurements (corresponding sides) as the preimage.
There are three isometric transformations: translation, reflection, and rotation.
Dilation is NOT AN ISOMETRIC TRANSFORMATION, because the measurements of the sides are not the same.
Now that the similarities of the transformations have been addressed, it is time to learn the specifics of each.
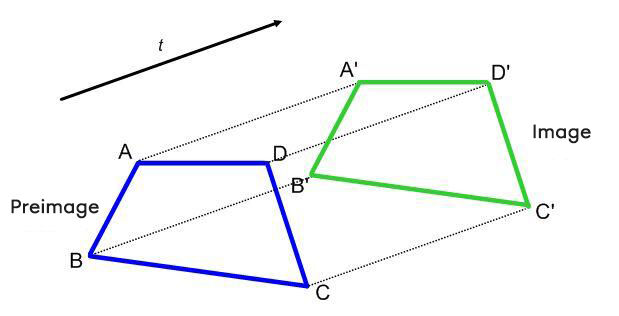
Roughly speaking, a translation is simply moving a figure by "sliding" it without changing its orientation.
During a translation, the figure (preimage) slides a certain distance. The image retains the same characteristics as the initial figure (side and angle measurements). This is an isometric transformation.
To learn more about translations, click on the following links:
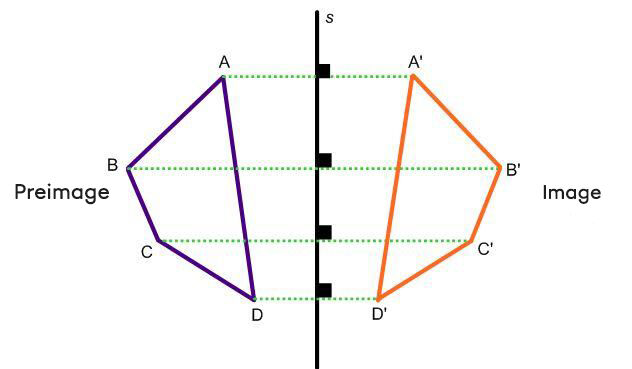
This geometric transformation can be compared to a reflection in a mirror.
A reflection is a geometric transformation where the image mirrors the preimage. Using this definition, the image is the reversal – or flip – of the preimage.
To learn more about reflections, click on the following links:
As the name suggests, a figure is rotated or turned to change its orientation.
A rotation is a geometric transformation that involves rotating a figure around a point or an axis.
To learn more about rotations, click on the following links:
Dilation is the only geometrical transformation which modifies the characteristics of the initial figure (preimage).
Dilation is a geometric transformation that consists of enlarging or reducing a figure according to a scale factor and centre.
The image figure obtained by a dilation retains the same interior angle measurements. However, the corresponding sides do not have the same length. Instead, the ratio of corresponding sides remains constant.
To learn more about dilation, consult the following links: