Sometimes, it can be useful to switch from a periodic number to a fraction or vice versa. The following concept sheet discusses the methods for successfully performing these switches.
Before presenting the methods, review the definition of period.
When a group of numbers written in decimal notation repeat indefinitely, it is called a period. When the numbers are written, identify the first period after the decimal point by drawing a horizontal bar above it.
Here are some examples of periods.
||\begin{align}0.666666666...&=0.\overline{6}\\
0.345252525...&=0.34\overline{52}\\
3.636363636...&=3.\overline{63}\\
0.714285714...&=0.\overline{714285}\end{align}||
When expressing a fraction in decimal notation, the division of the numerator by the denominator may never end. This creates a period.
-
Divide the numerator by the denominator.
-
Determine the period.
-
Write the number in decimal notation using the horizontal bar above the period.
Express the fraction |\displaystyle\frac{5}{6}| in decimal notation.
-
Divide the numerator by the denominator.
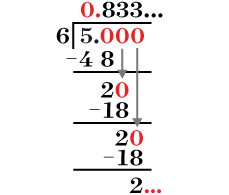
Notice that the |3| repeats itself indefinitely.
-
Determine the period.
||0.8\underbrace{\color{blue}{3}}_{\color{blue}{\text{period}}}33...|| -
Write the number in decimal notation using the horizontal bar above the period.
Thus, we get |\displaystyle \frac{5}{6}=0.8\overline{3}|
Express the fraction |\displaystyle \frac{19}{11}| in decimal notation.
-
Divide the numerator by the denominator.
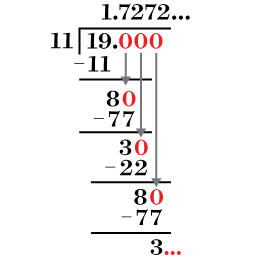
Notice that the |72| repeats indefinitely.
-
Determine the period.
||1,\underbrace{\color{blue}{72}}_{\color{blue}{\text{period}}}72...|| -
Write the number in decimal notation using the horizontal line above the period.
Thus, we get |\displaystyle \frac{19}{11}=1.\overline{72}|
The method of switching from a periodic number in decimal notation to its fractional notation is more complex and requires the use of algebra.
-
Define the periodic number as a variable. Multiply the number by the power of |10| that places the decimal immediately before the first period (or repeating part), if necessary.
-
Multiply the number by the power of |10| that places the decimal immediately before the first period (or repeating part).
-
Subtract the number from step 1 from the number from step 2 to obtain an integer or whole number.
-
Isolate the variable and simplify the fraction.
We will differentiate two particular cases in the examples. In the first case, the period will be directly after the decimal point. In a second case, the period will be separated from the decimal point by at least one digit. Step 1 will be slightly different in these two cases.
Express |0.\overline{36}| in fractional notation.
-
Define the periodic number as a variable. Multiply the number by the power of |10| that places the decimal immediately before the first period (or repeating part), if necessary. ||n=0.\overline{36}|| Since the period is already located to the right of the decimal point, we go directly to step 2.
-
Multiply the number by the power of |10| that places the decimal immediately after the first period (or repeating part). ||\begin{align}n\times 100&=0.\overline{36}\times 100\\ 100n&=36.\overline{36}\end{align}||
-
Subtract the number from step 1 from the number from step 2 to obtain an integer or whole number. ||\begin{align}100n-\color{red}{n}&=36.\overline{36}-\color{red}{0.\overline{36}} & &(\text{The decimal part cancels out.})\\ 99n&=36\end{align}||
-
Isolate the variable and simplify the fraction. ||\begin{align}99n=36\Rightarrow n&=\frac{36}{99}\\ n&=\frac{4}{11}\end{align}||
Thus, we get |\displaystyle 0.\overline{36}=\frac{4}{11}|.
Express |1.5\overline{24}| in fractional notation.
-
Define the periodic number as a variable. Multiply the number by the power of |10| that places the decimal immediately before the first period (or repeating part) if necessary.||n=1.5\overline{24}|| Note that the period is not located next to the decimal point.
Therefore, we must multiply by |10| to move it. ||\begin{align}n\times 10&=1.5\overline{24}\times 10\\ 10n&=15.\overline{24}\end{align}|| -
Multiply the number by the power of |10| that places the decimal immediately after the first period (or repeating part).||\begin{align}n\times 1000&=1.5\overline{24}\times 1000\\ 1000n&=1524.\overline{24}\end{align}||
-
Subtract the number from step 1 from the number from step 2 to obtain an integer or whole number.||\begin{align}1000n-\color{red}{10n}&=1524.\overline{24}-\color{red}{15.\overline{24}} & &(\text{The decimal part cancels out.})\\ 990n&=1509\end{align}||
-
Isolate the variable and simplify the fraction.||\begin{align}990n=1\ 509\Rightarrow n&=\dfrac{1\ 509}{990}\\ n&=\dfrac{503}{330}\end{align}||
Thus, we get |\displaystyle 1.5\overline{24}=\frac{503}{330}|.