Dans certaines situations, il peut être utile de passer d'un nombre périodique à une fraction ou l'inverse. La fiche suivante traite des méthodes à utiliser pour effectuer ces passages avec succès.
Avant de présenter ces méthodes, il convient de rappeler la définition de période.
Pour les nombres écrits en notation décimale, une période correspond à un groupe de chiffres qui se répètent sans fin. Lorsqu'on écrit ces nombres, on identifie la première période après la virgule en traçant un trait horizontal au-dessus de celle-ci.
Voici quelques exemples de périodes.||\begin{align} 0{,}666666666...&=0{,}\overline{6}\\
0{,}345252525...&=0{,}34\overline{52}\\
3{,}636363636...&=3{,}\overline{63}\\
0{,}714285714...&=0{,}\overline{714285}\end{align}||
Lorsqu'on tente d'exprimer une fraction en notation décimale en effectuant la division du numérateur par le dénominateur, il se peut que la division ne se termine jamais, créant ainsi une période.
-
Effectuer la division du numérateur par le dénominateur.
-
Déterminer la période.
-
Écrire le nombre en notation décimale en utilisant le trait horizontal au-dessus de la période.
Exprime la fraction |\dfrac{5}{6}| en notation décimale.
-
Effectuer la division du numérateur par le dénominateur.
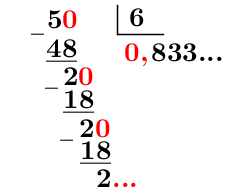
On remarque que le |3| se répète indéfiniment.
-
Déterminer la période.||0,8\underbrace{\color{blue}{3}}_{\color{blue}{\text{période}}}33...||
-
Écrire le nombre en notation décimale en utilisant le trait horizontal au-dessus de la période.
On a donc |\dfrac{5}{6}=0{,}8\overline{3}.|
Exprime la fraction |\dfrac{19}{11}| en notation décimale.
-
Effectuer la division du numérateur par le dénominateur.
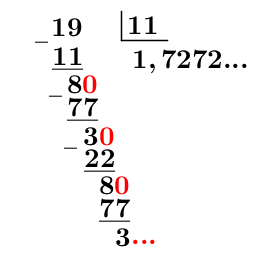
On remarque que le |72| se répète indéfiniment.
-
Déterminer la période.||1,\underbrace{\color{blue}{72}}_{\color{blue}{\text{période}}}72...||
-
Écrire le nombre en notation décimale en utilisant le trait horizontal au-dessus de la période.
On a donc |\dfrac{19}{11}=1{,}\overline{72}.|
La méthode pour passer d'un nombre périodique en notation décimale à sa représentation en notation fractionnaire est un peu plus complexe que les autres. Cette méthode fait intervenir l'algèbre.
-
Définir le nombre périodique comme une variable. Si la période n'est pas collée à droite de la virgule, multiplier par une puissance de |10| pour qu'elle le soit.
-
Multiplier le nombre périodique par une puissance de |10| pour que la période devienne entière.
-
Soustraire le nombre de l'étape 1 du nombre de l'étape 2 pour obtenir un entier.
-
On isole la variable et on simplifie la fraction.
On différenciera deux cas particuliers pour les exemples. Dans un premier cas, la période sera « collée » sur la virgule. Dans un deuxième cas, la période sera séparé de la virgule par au moins un chiffre. La démarche de l'étape 1 sera légèrement différente pour les deux cas.
Exprime |0{,}\overline{36}| en notation fractionnaire
-
Définir le nombre périodique comme une variable. Si la période n'est pas collée à droite de la virgule, multiplier par une puissance de |10| pour qu'elle le soit. ||n=0{,}\overline{36}||Comme la période est collée à droite de la virgule, on passe à l'étape 2.
-
Multiplier le nombre périodique par une puissance de |10| pour que la période devienne entière. ||\begin{align}n\times 100&=0{,}\overline{36}\times 100\\ 100n&=36{,}\overline{36}\end{align}||
-
Soustraire le nombre de l'étape 1 du nombre de l'étape 2 pour obtenir un entier. ||\begin{align}100n-\color{red}{n}&=36{,}\overline{36}-\color{red}{0{,}\overline{36}} & &(\text{La partie décimale s'annule.})\\ 99n&=36\end{align}||
-
On isole la variable et on simplifie la fraction. ||\begin{align}99n=36\Rightarrow n&=\frac{36}{99}\\ n&=\frac{4}{11}\end{align}||
On a donc |0{,}\overline{36}=\dfrac{4}{11}.|
Exprime |1{,}5\overline{24}| en notation fractionnaire.
-
Définir le nombre périodique comme une variable. Si la période n'est pas collée à droite de la virgule, multiplier par une puissance de |10| pour qu'elle le soit. ||n=1{,}5\overline{24}||On remarque que la période n'est pas collée sur la virgule.
On devra donc multiplier par |10| pour qu'elle le soit. ||\begin{align}n\times 10&=1{,}5\overline{24}\times 10\\ 10n&=15{,}\overline{24}\end{align}|| -
Multiplier le nombre périodique par une puissance de |10| pour que la période devienne entière. ||\begin{align}n\times 1\ 000&=1,5\overline{24}\times 1\ 000\\ 1\ 000n&=1\ 524{,}\overline{24}\end{align}||
-
Soustraire le nombre de l'étape 1 du nombre de l'étape 2 pour obtenir un entier. ||\begin{align}1\ 000n-\color{red}{10n}&=1\ 524{,}\overline{24}-\color{red}{15{,}\overline{24}} & &(\text{La partie décimale s'annule.})\\ 990n&=1\ 509\end{align}||
-
On isole la variable et on simplifie la fraction. ||\begin{align}990n=1\ 509\Rightarrow n&=\dfrac{1\ 509}{990}\\ n&=\dfrac{503}{330}\end{align}||
On a donc |1{,}5\overline{24}=\dfrac{503}{330}.|