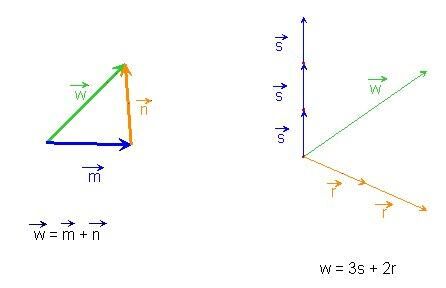
Even if there is an infinity of vectors, it is possible to express them as a combination of vectors. Therefore, the vectors used to create the combination form basis vectors.
The basis vectors are a set of vectors which enable other vectors to be expressed using a linear combination.
To compose a basis vector, select any vectors |\overrightarrow {u}| and |\overrightarrow{v}| as long as they are not parallel (|\overrightarrow{u} \not\parallel \overrightarrow{v}|).
Two-dimensional vectors can be decomposed into a sum of two other vectors, which are multiplied by scalars.
|\overrightarrow{u_1}| and |\overrightarrow{u_2}| are two non-parallel vectors, and |a| and |b| are two scalars. Therefore:
||\overrightarrow{v} = a \overrightarrow{u_1} + b \overrightarrow{u_2}||
To create the vector |\overrightarrow {v},| we use a combination of vectors |\overrightarrow{u_1}| and |\overrightarrow{u_2},| i.e., a vector combination.
To determine a linear combination using the vector components to be decomposed as well as the basis vectors, follow these steps.
-
Write the linear combination using the components of the vectors, and use scalars (e.g., |a| and |b|) to multiply the basis vectors.
-
Write a system of two equations with two unknowns: one equation for the components in |x| and one for the ones in |y|.
-
Solve the system of equations.
-
Write the linear combination by replacing the constants |a| and |b| with the values determined in step 3.
The result resembles the following.
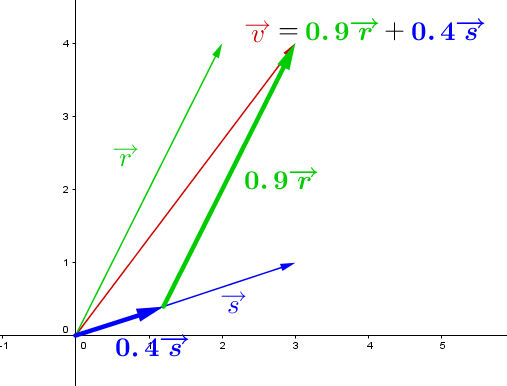
What is the vector combination that results in the vector |\overrightarrow{v}= (3,4),| as a function of vectors |\overrightarrow{s} = (3,1)| and |\overrightarrow{r}=(2,4)?|
-
Write the linear combination
First, write an equation representing the linear combination using constants |a| and |b,| which are scalars multiplying the vectors |\overrightarrow{r}| and |\overrightarrow{s}.|
||\begin{align} \overrightarrow {v} &= a \overrightarrow{s} + b \overrightarrow {r} \\
\Rightarrow (3, 4) &= a(3, 1) + b(2, 4) \\
&= (3a, a) + (2b, 4b) \end{align}||
Group the components in |x| and |y| together.
||\Rightarrow (3, 4) = (3a + 2b , a + 4b) || -
Create the system of equations
According to the component in |x| of |\overrightarrow {v},| the result is:
||3 = 3a + 2b||
According to the component in |y| of |\overrightarrow {v},| the result is:
||4 = a + 4b||
Finally, the result is the following system of equations:
||\left\{\begin{matrix}
3=3a+2b\\
4=a+4b
\end{matrix}\right.|| -
Solve the system of equations
Solve the system using the elimination method.Multiplying the second equation by |3| results in:
||3(4)=3(a+4b) \rightarrow 12 = 3a + 12b||
Next, eliminate the terms with the variable |a.|
||\begin{align}3&=3a+2b\\-\ (12&=3a+12b)\\ \hline -9 &= -10b \end{align}||
Isolating |b,| the result is:
||0.9 = b||
Replace the constant |b| in one of the two starting equations to determine the constant |a.|
||\begin{align} 3 &= 3a +2 \times 0.9 \\
3 &= 3a + 1.8 \\
1.2 &= 3a\\
0.4 &= a \end{align}|| -
Write the desired linear combination
||\begin{align} \overrightarrow {v} &= a \overrightarrow{s} + b \overrightarrow {r} \\
&=0.4\overrightarrow{s}+0.9\overrightarrow{r}\end{align}||
Use a Cartesian plane and integrate the information on each of the vectors |\overrightarrow {v}, \overrightarrow {s}| and |\overrightarrow{r}| to confirm the answer.
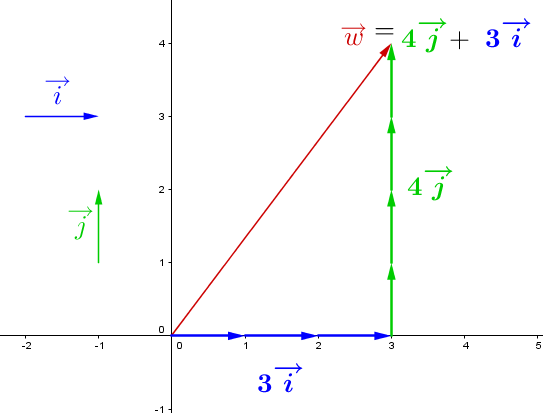
The orthonormal basis vector
There are two perpendicular vectors which serve as the base for several vectors. The vectors are perpendicular and unitary. They are often identified as |\overrightarrow{i}| and |\overrightarrow{j}.|
|\overrightarrow{i}| is horizontal and has the components |(1,0),| while |\overrightarrow{j}| is vertical and has the components |(0,1).| Vectors |\overrightarrow{i}| and |\overrightarrow{j}| form the orthonormal basis vectors from which it is easiest to construct vector combinations.
To verify your understanding of vectors, consult the following interactive CrashLesson:
