Each mathematical operation has an inverse. By using the inverse or reciprocal of a function, it is possible to solve almost any type of equation. In the case of logarithmic notation, it is the reciprocal of exponential notation. Thus, when the variable that needs to be isolated is an exponent, logarithms can be used.
The application of the definition and the laws of logarithms are used in financial mathematics for resolving situations involving compound interest.
The following concept sheet is essential for the study of exponential and logarithmic functions.
A logarithm is an exponent where another number called the base of the logarithm must be assigned to obtain a given number (argument).
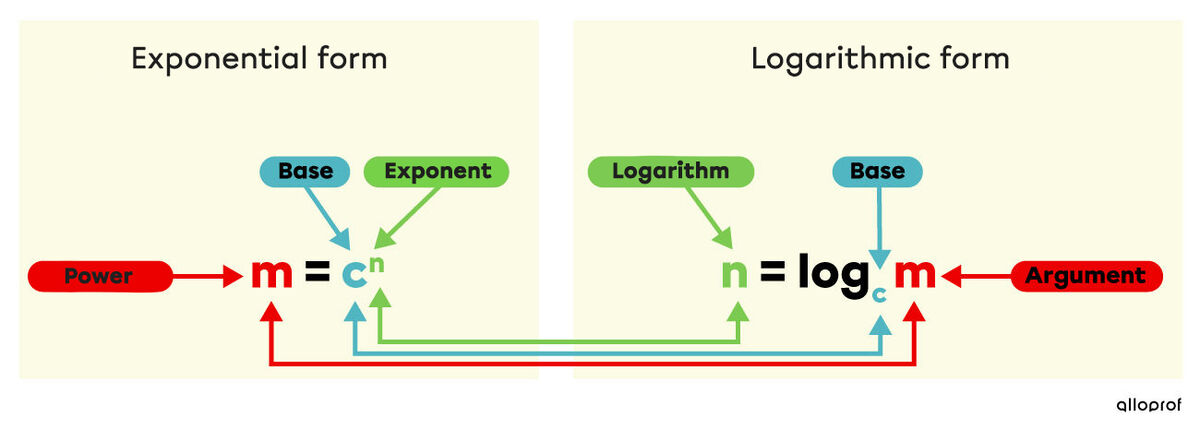
What exponent should be attributed to the base |c| to get the number |m|? This is what the logarithm calculates.
Note: It is important to master the vocabulary when in exponential or logarithmic form.
In some situations, the logarithm’s argument is called the power.
By definition of the logarithm, we get |c^{\log_c m} = m|.
Several bases exist. The two most common bases used are:
-
By convention, when the logarithm’s base is 10, it is not written: |\log_{10}m=\log m.|
-
The natural logarithm is used quite often. It is, in fact, a logarithm where the base is the number |e=2{.}718\,281\,828\dots| The number is irrational, i.e., its decimal never repeats and never terminates. When the logarithm’s base is |e,| write |\ln | rather than |\log_e.|
Finally, regardless of the base used, |m \neq 0| since there is no real value other than |c^n=0|.
The logarithm’s base |c| must meet two conditions:
-
|c>0|
-
|c \neq 1|
The logarithm’s argument |m| must be greater than 0.
Example 1
||\begin{align} \log_\color{blue}{2} \ \color{red}{8}\ &\Rightarrow & \small \text{What} \ &\small \color{green}{exponent} \ \small \text{must we apply to the} \ \color{blue}{base} \ \small \text{to obtain the } \color{red}{argument} \small \text{?} \\
&\Rightarrow &\color{blue}{2}^\color{green}{?} &= \color{red}{8}\\
&\Rightarrow &\color{blue}{2}^\color{green}{?} &= \color{red}{2^3} \\
&\Rightarrow &\color{green}{?} &= 3 \end{align}||
Thus, the value of |\log_\color{blue}{2} \ \color{red}{8}=\color{green}{3}.|
Example 2
||\begin{align} \log_\color{blue}{3} \ \color{red}{243}\ &\Rightarrow & \small \text{What} \ &\small \color{green}{exponent} \ \small \text{must we apply to the} \ \color{blue}{base} \ \small \text{to obtain the } \color{red}{argument} \small \text{?} \\
&\Rightarrow &\color{blue}{3}^\color{green}{?} &= \color{red}{243}\\
&\Rightarrow &\color{blue}{3}^\color{green}{?} &= \color{red}{3^5} \\
&\Rightarrow &\color{green}{?} &= 5 \end{align}||
Thus, the value of |\log_\color{blue}{3} \ \color{red}{243}=\color{green}{5}.|
Example 3
||\begin{align} \log_\color{blue}{\frac{1}{4}} \ \color{red}{64} &\Rightarrow & \small \text{What} \ &\small \color{green}{exponent} \ \small \text{must we apply to the} \ \color{blue}{base} \ \small \text{to obtain the } \color{red}{argument} \small \text{?} \\
&\Rightarrow &\color{blue}{\left(\frac{1}{4}\right)}^\color{green}{?} &= \color{red}{64}\\
&\Rightarrow &\color{blue}{\left(\frac{1}{4}\right)}^\color{green}{?} &= \color{red}{4^3} \\
&\Rightarrow &\color{blue}{\left(\frac{1}{4}\right)}^\color{green}{?} &= \left(\frac{1}{4}\right)^{\text{- }3} \\
&\Rightarrow &\color{green}{?} &= \text{-}3 \end{align}||
Thus, the value of |\log_\color{blue}{\frac{1}{4}} \ \color{red}{64}=\color{green}{\text{-}3}.|
Unfortunately, it is not always possible to calculate a logarithm without using a calculator. The laws of logarithms enable us to do a lot of calculations.
To confirm that you understand the laws of logarithms and exponents, see the following interactive CrashLesson:
