The family of exponential functions includes all functions for which the independent variable |\boldsymbol{(x)}| is an exponent.
All exponential functions have an asymptote. Graphically, this means that exponential functions are represented by a curve that approaches a horizontal line without ever intersecting it.
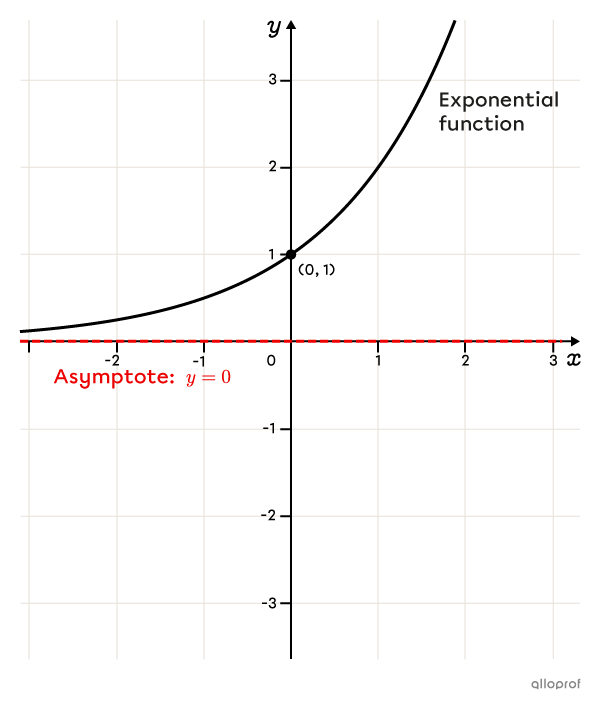
Exponential functions can be represented in one of the following forms.
Basic form||f(x)=c^x||
Simplified standard form||f(x)=a(c)^x||or||f(x)=a(c)^{bx}||
Standard form||f(x)=a(c)^{b(x-h)}+k||
The base |(c)| of an exponential function is always a number that is greater than |0| and not equal to |1.|
The exponential function is generally given in one of the 2 following forms.
||f(x)=a(c)^x||
||f(x)=a(c)^{bx}||
The rule for an exponential function written with parameters |a,| |b| and |c| can always be simplified to a rule that only contains parameters |a| and |c.| Here's the algebraic proof:||\begin{align}y&=a(c)^{bx}\\[3pt]&=a\left(\boldsymbol{\color{#3a9a38}{c^b}}\right)^x\\[3pt]&=a(\color{#7cca51}{\textbf{c}})^x\end{align}||In other words, any equation of the form |y=a(c)^{bx}| is equivalent to another equation of the form |y=a(\text{c})^x.|
The functions |y=24(2)^{3x}| and |y=24(8)^x| are equivalent. Here is the proof:||24(2)^{3x}=24\left(\boldsymbol{\color{#3a9a38}{2^3}}\right)^x=24(\boldsymbol{\color{#7cca51}{8}})^x||
When finding the rule of an exponential function, it's best to find it using the form |y=a(\text{c})^x.| This eliminates the need to find the value of parameter |b.|
A simplified exponential function always has the following characteristics:
-
One asymptote whose rule is |y=0|
-
No x-intercept (zero)
-
One y-intercept with coordinates |(0,a)|
In the following interactive animation, you can move the cursors to observe the roles of parameters |a,| |b| and |c.|
The standard form of an exponential function is as follows:
||f(x)=a(c)^{b(x-h)}+k||
The rule of an exponential function in standard form can always be simplified to a rule that only contains parameters |a,| |c| and |k.| Here's the algebraic proof:||\begin{align}y&=a(c)^{b(x-h)}+k\\[3pt]&=a\left(\boldsymbol{\color{#3a9a38}{c^b}}\right)^{x-h}+k\\[3pt]&=a(\color{#7cca51}{\textbf{c}})^{x-h}+k\\[3pt]&=a\dfrac{\text{c}^x}{\text{c}^h}+k\\[3pt]&=\boldsymbol{\color{#3b87cd}{\dfrac{a}{\textbf{c}^h}}}\text{c}^x+k\\[3pt]&=\color{#51b6c2}{\textbf{a}}(\text{c})^x+k\end{align}||In other words, any equation of the form |y=a(c)^{b(x-h)}+k| is equivalent to another equation of the form |y=\text{a(c)}^x+k.|
The functions |y=24(2)^{3(x-1)}+7| and |y=3(8)^x+7| are equivalent. Here is the proof:||\begin{align}24(2)^{3(x-1)}+7&=24\left(\boldsymbol{\color{#3a9a38}{2^3}}\right)^{x-1}+7\\[3pt]&=24(\boldsymbol{\color{#7cca51}{8}})^{x-1}+7\\[3pt]&=24\dfrac{8^x}{8^1}+7\\[3pt]&=\boldsymbol{\color{#3b87cd}{\dfrac{24}{8}}}8^x+7\\[3pt]&=\boldsymbol{\color{#51b6c2}{3}}(8)^x+7\end{align}||
When finding the rule of an exponential function, it's best to find it using the form |y=\text{a(c)}^x+k.| This eliminates the need to find the value of parameters |h| and |b.|
A standard exponential function always has the following characteristics:
-
One asymptote whose rule is |y=k|
-
One x-intercept (zero) if |k\ne0|
-
One y-intercept
In the following interactive animation, you can move the cursors to observe the roles of parameters |a,| |b,| |c,| |h| and |k.|