|
Arithmetic and algebra |
Geometry | Analytic geometry | Probability and statistics |
|---|---|---|---|
|
Expressing a Number as a Percentage |
The Perimeter and Area of Plane Figures |
|
||\dfrac{\text{numerator}}{\text{denominator}}\times100|| |
||\dfrac{\text{numerator}}{\text{denominator}}=\dfrac{\text{number sought}}{100}|| |
|
Property |
Addition |
Multiplication |
|---|---|---|
|
||a+b=b+a|| |
||a\times b=b\times a|| |
|
||(a+b)+c=a+(b+c)|| |
||(a\times b)\times c=a\times(b\times c)|| |
|
||a+0=0+a=a|| |
||a\times1=1\times a=a|| |
|
|
||a\times0=0\times a=0|| |
|
||a+-a=-a+a=0|| |
||a\times\dfrac{1}{a}=1|| |
|
||a\times(b\pm c)=a\times b\pm a\times c|| |
|
|
Functions |
Basic rule |
Transformed rule |
||
|---|---|---|---|---|
|
0 Degree |
||y=b|| |
|
||
|
1st degree |
||y=x|| |
Functional form |
Symmetrical form |
General form |
|
||y=ax+b|||a|: rate of change (slope) |b|: y-intercept||a=\dfrac{y_2-y_1}{x_2-x_1}|| |
||\dfrac{x}{a}+\dfrac{y}{b}=1|||a|: x-intercept |b|: y-intercept |
||Ax+By+C=0|| |
||
|
|\Rightarrow| Symmetrical||\begin{align}a_s&=\dfrac{-b_f}{a_f}\\b_s&=b_f\end{align}|| |
|\Rightarrow| Functional||\begin{align}a_f&=\dfrac{-b_s}{a_s}\\b_f&=b_s\end{align}|| |
|\Rightarrow| Functional||\begin{align}a_f&=\dfrac{-A}{B}\\b_f&=\dfrac{-C}{B}\end{align}|| |
||
|
|\Rightarrow| General Find the common denominator and bring everything to the same side of the equation. |
|\Rightarrow| General Find the common denominator and bring everything to the same side of the equation. |
|\Rightarrow| Symmetrical||\begin{align}a_s&=\dfrac{-C}{A}\\\\b_s&=\dfrac{-C}{B}\end{align}|| |
||
|
2nd degree |
||y=x^2|| |
General form |
Standard form |
Factored form |
|
||y=ax^2+bx+c|| |
||\begin{align}y&=\text{a}\big(b(x-h)\big)^2+k\\y&=\text{a }b^2(x-h)^2+k\\y&=a(x-h)^2+k\end{align}|| |
Two zeros||y=a(x-z_1)(x-z_2)||One unique zero||y=a(x-z_1)^2|| |
||
|
Number of zeros||\sqrt{b^2-4ac}|| |
Number of zeros||\sqrt{\dfrac{-k}{a}}|| |
Number of zeros Note: if there are no zeros, it's not possible to use this form. |
||
|
Value of the zeros||\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}|| |
Value of the zeros||h\pm\sqrt{\dfrac{-k}{a}}|| |
Value of the zeros |z_1| and |z_2| |
||
|
Absolute value |
||y=\vert x\vert|| |
Standard form |
||
|
||\begin{align}y&=\text{a }\vert b(x-h)\vert+k\\y&=\text{a }\vert b\vert\times\vert x-h\vert+k\\y&=a\ \vert x-h\vert+k\end{align}|| |
||||
|
Square root |
||y=\sqrt{x}|| |
Standard form |
||
|
||\begin{align}y&=\text{a}\sqrt{b(x-h)}+k\\[3pt]y&=\text{a}\sqrt b\sqrt{\pm(x-h)}+k\\[3pt]y&=a\sqrt{\pm(x-h)}+k\end{align}|| |
||||
| Step (greatest integer) function | ||y=[x]|| | Standard form | ||
| ||y=a\big[b\,(x-h)\big]+k|| | ||||
|
Functions |
Basic rule |
Transformed rule |
Definitions and laws |
|---|---|---|---|
|
Exponential |
||f(x)=c^x|| |
||f(x)=a(c)^{b(x-h)}+k|| |
||\begin{align}a^0&=1\\[3pt]a^1&=a\\[3pt]a^{-m}&=\dfrac{1}{a^m}\\[3pt]a^{^{\frac{\large{m}}{\large{n}}}}&=\sqrt[\large{n}]{a^m}\\[3pt]a^m=a^n&\!\!\ \Leftrightarrow\ m=n\\[3pt]a^ma^n&=a^{m+n}\\[3pt]\dfrac{a^m}{a^n}&=a^{m-n}\\[3pt](ab)^m&=a^mb^m\\[3pt](a^m)^{^{\Large{n}}}&=a^{mn}\\[3pt]\left(\dfrac{a}{b}\right)^m&=\dfrac{a^m}{b^m}\\[3pt]\sqrt[\large{n}]{ab}&=\sqrt[\large{n}]{a}\ \sqrt[\large{n}]{b}\\[3pt]\sqrt[\large{n}]{\dfrac{a}{b}}&=\dfrac{\sqrt[\large{n}]{a}}{\sqrt[\large{n}]{b}}\end{align}|| |
|
Logarithmic |
||f(x)=\log_cx|| |
||f(x)=a\log_c(b(x-h))+k|| |
||\begin{align}\log_c1&=0\\[3pt]\log_cc&=1\\[3pt]c^{\log_{\large{c}}m}&=m\\[3pt]\log_cc^m&=m\\[3pt]\log_cm=\log_cn\ &\Leftrightarrow\ m=n\\[3pt]\log_c(mn)&=\log_cm+\log_cn\\[3pt]\log_c\left(\dfrac{m}{n}\right)&=\log_cm-\log_cn\\[3pt]\log_c(m^n)&=n\log_cm\\[3pt]\log_cm&=\dfrac{\log_sm}{\log_sc}\end{align}|| |
|
One is the inverse of the other||x=c^y\ \Longleftrightarrow\ y=\log_cx|| |
|||
|
Functions |
Basic rule |
Transformed rule |
Special characteristics |
|---|---|---|---|
|
Sine |
||f(x)=\sin x|| |
||f(x)=a\sin\big(b(x-h)\big)+k|| |
||\begin{align}\vert a\vert&=\dfrac{\max-\min}{2}\\[3pt]\vert b \vert&=\dfrac{2\pi}{\text{period}}\\[3pt]\text{Range}f&=[k-a,k+a]\end{align}||Zeros: An infinite number of the form |(x_1+nP)| and |(x_2+nP)| where |x_1| and |x_2| are consecutive zeros, |n\in\mathbb{Z}| and |P| is the period. |
|
Cosine |
||f(x)=\cos x|| |
||f(x)=a\cos\big(b(x-h)\big)+k|| |
|
|
Tangent |
||f(x)=\tan x|| |
||f(x)=a\tan\big(b(x-h)\big)+k|| |
||\vert b\vert=\dfrac{\pi}{\text{period}}\\[3pt]\text{Dom}\ f=\mathbb{R}\backslash\left\{\left(h+\dfrac{P}{2}\right)+nP\right\}||where |n\in\mathbb{Z}| and |P| is the period. Zeros: An infinite number of the form |x_1+nP| where |x_1| is a zero, |n\in\mathbb{Z}| and |P| is the period. |
|
Arcsine |
||f(x)=\arcsin(x)||or||f(x)=\sin^{-1}(x)|| |
||f(x)=a\arcsin\big(b(x-h)\big)+k|| |
|
|
Arccosine |
||f(x)=\arccos(x)||or||f(x)=\cos^{-1}(x)|| |
||f(x)=a\arccos\big(b(x-h)\big)+k|| |
|
|
Arctangent |
||f(x)=\arctan(x)||or||f(x)=\tan^{-1}(x)|| |
||f(x)=a\arctan\big(b(x-h)\big)+k|| |
|
|
Basic identities |
|||||
|---|---|---|---|---|---|
|
||\sin^2\theta+\cos^2\theta=1|| |
||1+\tan^2\theta=sec^2\theta|| |
||1+\text{cotan}^2\theta=\text{cosec}^2\theta|| |
|||
|
Other identities |
|||||
|
||\begin{align}\sin(a+b)&=\sin a\cos b+\cos a\sin b\\[3pt]\sin(a-b)&=\sin a\cos b-\cos a\sin b\\[3pt]\cos(a+b)&=\cos a\cos b-\sin a\sin b\\[3pt]\cos(a-b)&=\cos a\cos b+\sin a\sin b\\[3pt]\tan(a+b)&=\dfrac{\tan a+\tan b}{1-\tan a\tan b}\\[3pt]\tan(a-b)&=\dfrac{\tan a-\tan b}{1+\tan a\tan b}\end{align}|| |
||\begin{align}\sin2x&=2\sin x\cos x\\[3pt]\cos2x&=1-2\sin^2x\\[3pt]\tan2x&=\dfrac{2}{\text{cotan}x-\tan x}\\[3pt]\sin(-\theta)&=-\sin\theta\\[3pt]\cos(-\theta)&=\cos\theta\\[3pt]\sin\left(\theta+\dfrac{\pi}{2}\right)&=\cos\theta\\[3pt]\cos\left(\theta+\dfrac{\pi}{2}\right)&=-\sin\theta\end{align}|| |
||||
| |\text{km}| | |\text{hm}| | |\text{dam}| | |\text{m}| | |\text{dm}| | |\text{cm}| | |\text{mm}| |
| In this direction |\Rightarrow \times 10\qquad \qquad\qquad| In this direction |\Leftarrow \div 10| | ||||||
| |\text{km}^2| | |\text{hm}^2| | |\text{dam}^2| | |\text{m}^2| | |\text{dm}^2| | |\text{cm}^2| | |\text{mm}^2| |
| In this direction |\Rightarrow \times 100\qquad \qquad\qquad| In this direction |\Leftarrow \div 100| | ||||||
| |\text{km}^3| | |\text{hm}^3| | |\text{dam}^3| | |\text{m}^3| | |\text{dm}^3| | |\text{cm}^3| | |\text{mm}^3| |
| In this direction |\Rightarrow \times 1000\qquad \qquad\qquad| In this direction |\Leftarrow \div 1000| | ||||||
|
Figure |
Perimeter |
Area |
|
|---|---|---|---|
|
Triangle |
The sum of all sides |
|A =\dfrac{b\times h}{2}| |A = \sqrt{p(p-a)(p-b)(p-c)}| |A=\dfrac{ab\sin C}{2}| |
|
|
Square |
|P=4 \times s| |
|\begin{align} A &= s \times s\\ |
|
|
Rectangle |
|\begin{align} P &= b+h+b+h\\ |
|A=bh| |
|
|
Rhombus |
P=|4 \times s| |
|A=\dfrac{D\times d}{2}| |
|
|
Parallelogram |
The sum of all sides |
|A=bh| |
|
|
Trapezoid |
The sum of all sides |
|A=\dfrac{(B+b)\times h}{2}| |
|
|
Regular polygon |
|P=n \times s| |
|A=\dfrac{san}{2}| |
|
|
Any polygon |
The sum of all sides |
The sum of the areas of all the triangles that make up the polygon |
|
|
Circle |
|\begin{align} d &= 2r\\\\ |
||\begin{align} C &= \pi d\\\\ |
|A=\pi r^2| |
|
Circular arc and sector of a circle |
|\displaystyle \frac{\text{Central angle}}{360^o}=\frac{\text{Arc length}}{2\pi r}| |
|\displaystyle \frac{\text{Central angle}}{360^o}=\frac{\text{Area of sector}}{\pi r^2}| |
|
|
Theorems in a circle |
|---|
|
Theorems related to radii, diameters, chords and arcs:
Theorems related to angles:
Theorems relating to the secants and tangents of the circle:
|
|
Total number of diagonals |
Number of diagonals at each vertex |
Sum of the measures of the interior angles |
Measure of an interior angle |
|---|---|---|---|
|
|\dfrac{n(n-3)}{2}| |
|n-3| |
|180(n-2)| |
|\dfrac{180(n-2)}{n}| |
|
Solids |
Lateral area |
Total area |
Volume |
|---|---|---|---|
|
Prism and cylinder |
Sum of the areas of the lateral faces of the solid |A_L=P_b\times h| |
Sum of the areas of all faces of the solid |A_T = A_L+2A_b| |
|V=A_b\times h| |
|
Pyramid and cone |
Sum of the areas of the lateral faces of the solid |A_L=\displaystyle \frac{P_b\times a}{2}| |
Sum of the areas of all faces of the solid |A_T = A_L+A_b| |
|V=\displaystyle \frac{A_b\times h}{3}| |
|
Sphere |
|A=4\pi r^2| |
|V=\displaystyle \frac{4\pi r^3}{3}| |
|
|
Theorems in a right triangle |
|---|
|
|
Metric Relations in a Right Triangle |
|
Altitude to Hypotenuse theorem Product of the Sides theorem Proportional Mean theorem |
|
Trigonometric ratios |
Trigonometric laws (any triangle) |
|
|---|---|---|
| ||\sin A=\dfrac{\text{Opposite}}{\text{Hypotenuse}}|| | ||\text{csc }A=\dfrac{1}{\sin A}=\dfrac{\text{Hypotenuse}}{\text{Opposite}}|| | ||\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}|| |
| ||\cos A=\dfrac{\text{Adjacent}}{\text{Hypotenuse}}|| | ||\text{sec }A=\dfrac{1}{\cos A}=\dfrac{\text{Hypotenuse}}{\text{Adjacent}}|| | ||\begin{align}a^2&=b^2+c^2-2bc\cos A\\[3pt]b^2&=a^2+c^2-2ac\cos B\\[3pt]c^2&=a^2+b^2-2ab\cos C\end{align}|| |
| ||\tan A=\dfrac{\text{Opposite}}{\text{Adjacent}}|| | ||\text{cotan}A=\dfrac{1}{\tan A}=\dfrac{\text{Adjacent}}{\text{Opposite}}|| | |
|
Similarity ratio (Scale factor) |
Area ratio |
Volume ratio |
|---|---|---|
|
||k=\dfrac{\text{Length of image figure}}{\text{Length of initial figure}}|| |
||k^2=\dfrac{\text{Area of image figure}}{\text{Area of initial figure}}|| |
||k^3=\dfrac{\text{Volume of image solid}}{\text{Volume of initial solid}}|| |
|
Vector components |\boldsymbol{(a,b)}| |
|||
|---|---|---|---|
|
||a=\Vert \overrightarrow{u}\Vert \cos \theta|| ||b=\Vert \overrightarrow{u}\Vert \sin \theta|| |
Consider the vector |\overrightarrow{AB}| where |A(x_1, y_1)| and |B(x_2, y_2)| The components are: ||a=x_2-x_1\\b=y_2-y_1|| |
||
|
Magnitude (norm) of a vector |
|||
|
Consider the vector |\overrightarrow{u}=(a,b)| The magnitude is: ||\Vert\overrightarrow{v}\Vert=\sqrt{a^2+b^2}|| |
Consider the vector |\overrightarrow{AB}| where |A(x_1, y_1)| and |B(x_2, y_2)| The magnitude is: ||\Vert\overrightarrow{AB}\Vert=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}|| |
||
|
Direction (orientation) of a vector |
|||
|
|\theta=\tan^{-1}\left(\displaystyle\frac{b}{a}\right)| |
|
||
|
Adding two vectors |
|||
|
Consider |\overrightarrow{u}=(a,b)| and |\overrightarrow{v}=(c,d)| Therefore, |\overrightarrow{u}+\overrightarrow{v}=(a+c,b+d)| |
|\Vert \overrightarrow{u}+\overrightarrow{v}\Vert=\Vert \overrightarrow{u}\Vert+\Vert \overrightarrow{v}\Vert-2\Vert \overrightarrow{u}\Vert\ \Vert \overrightarrow{v}\Vert\ \cos\theta| where |\theta =\ \Large{\mid} \normalsize 180^o - \mid \theta_\overrightarrow{u}-\theta_\overrightarrow{v}\mid \Large{\mid}| |
||
|
Subtracting two vectors |
|||
|
Consider |\overrightarrow{u}=(a,b)| and |\overrightarrow{v}=(c,d)| Therefore, |\overrightarrow{u}-\overrightarrow{v}=(a-c,b-d)| |
|\Vert \overrightarrow{u}+\overrightarrow{v}\Vert=\Vert \overrightarrow{u}\Vert+\Vert \overrightarrow{v}\Vert-2\Vert \overrightarrow{u}\Vert\ \Vert \overrightarrow{v}\Vert\ \cos\theta| where |\theta=\mid \theta_\overrightarrow{u}-\theta_\overrightarrow{v}\mid| if |\mid \theta_\overrightarrow{u}-\theta_\overrightarrow{v}\mid<180^o| |
||
|
Scalar multiplication |
|||
|
Consider scalar |k| and vector |\overrightarrow{u}=(a,b)| Therefore, |k\overrightarrow{u}=(ka,kb)| |
|||
|
Scalar (dot) product |
|||
|
If the scalar product equals |0,| the vectors are perpendicular. |
|||
|
Using components Consider |\overrightarrow{u}=(a,b)| and |\overrightarrow{v}=(c,d)| Then, |\overrightarrow{u}\cdot \overrightarrow{v}=ac+bd| |
Using the magnitude and direction |\overrightarrow{u}\cdot \overrightarrow{v}=\Vert\overrightarrow{u}\Vert\times \Vert\overrightarrow{v}\Vert\times \cos\theta| |
||
|
Properties of the addition of two vectors |
|||
|
1) The sum of two vectors is a vector. |
|
||
|
2) Commutativity |
|\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u}| |
||
|
3) Associativity |
|(\overrightarrow{u} + \overrightarrow{v}) + \overrightarrow{w} = \overrightarrow{u} + (\overrightarrow{v} + \overrightarrow{w})| |
||
|
4) Existence of a neutral (identity) element |
|\overrightarrow{u}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{u}=\overrightarrow{u}| |
||
|
5) Existence of opposites |
|\overrightarrow{u}+(-\overrightarrow{u})=-\overrightarrow{u}+\overrightarrow{u}=\overrightarrow{0}| |
||
|
Properties of scalar multiplication |
|||
|
1) The product of a vector and a scalar is always a vector. |
|
||
|
2) Associativity |
|k_1(k_2\overrightarrow{u})=(k_1k_2)\overrightarrow{u}| |
||
|
3) Existence of a neutral (identity) element |
|1\times \overrightarrow{u}=\overrightarrow{u}\times 1=\overrightarrow{u}| |
||
|
4) Distributivity over vector addition |
|k(\overrightarrow{u}+\overrightarrow{v})=k\overrightarrow{u}+k\overrightarrow{v}| |
||
|
5) Distributivity over scalar addition |
|(k_1+k_2)\overrightarrow{u}=k_1\overrightarrow{u}+k_2\overrightarrow{v}| |
||
|
Properties of the scalar (dot) product |
|||
|
1) Commutativity |
|\overrightarrow{u}\cdot \overrightarrow{v}=\overrightarrow{v}\cdot \overrightarrow{u}| |
||
|
2) Scalar associativity |
|k_1\overrightarrow{u}\cdot k_2\overrightarrow{v}=k_1k_2(\overrightarrow{u}\cdot\overrightarrow{v})| |
||
|
3) Distributivity over a vector sum |
|\overrightarrow{u}\cdot(\overrightarrow{v}+\overrightarrow{w})=(\overrightarrow{u}\cdot\overrightarrow{v})+(\overrightarrow{u}\cdot\overrightarrow{w})| |
||
|
Concept |
Formulas |
|||||
|---|---|---|---|---|---|---|
|
Displacements |
||\begin{align}\Delta x&=x_2-x_1\\[3pt]\Delta y&=y_2-y_1\end{align}|| |
|||||
|
Distance between two points |
||d(A,B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}|| |
|||||
|
Division point formula |
Part-to-whole ratio |
Part-to-part ratio |
||||
|
||\begin{align}x_p&=x_1+\dfrac{r}{s}(x_2-x_1)\\[3pt]y_p&=y_1+\dfrac{r}{s}(y_2-y_1)\end{align}|| |
||\begin{align}x_p&=x_1+\dfrac{r}{r+s}(x_2-x_1)\\[3pt]y_p&=y_1+\dfrac{r}{r+s}(y_2-y_1)\end{align}|| |
|||||
|
Midpoint formula |
||(x_m,y_m)=\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)|| |
|||||
|
Slope (rate of change) of a line |
||a=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}|| |
|||||
|
Relative position of two lines with equations of the form |y=ax+b| |
Coinciding parallel lines |
Disjoint parallel lines |
Perpendicular lines |
|||
|
||\begin{align}a_1&=a_2\\[3pt]b_1&=b_2\end{align}|| |
||\begin{align}a_1&=a_2\\[3pt]b_1&\neq b_2\end{align}|| |
||a_1=-\dfrac{1}{a_2}|| |
||||
|
Transformation |
Rules |
Inverse |
|---|---|---|
|
Translation |
||t_{(a,b)}:(x,y)\stackrel{t}{\mapsto}(x+a,y+b)|| |
||t^{-1}_{(a,b)}=t_{(-a,-b)}:(x,y)\stackrel{t}{\mapsto}(x-a,y-b)|| |
|
Rotation |
||\begin{align}r_{(O,90^\circ)}&:(x,y)\stackrel{r}{\mapsto}(-y,x)\\[3pt]r_{(O,-270^\circ)}&:(x,y)\stackrel{r}{\mapsto}(-y,x)\\[3pt]r_{(O,180^\circ)}&:(x,y)\stackrel{r}{\mapsto}(-x,-y)\\[3pt]r_{(O,-90^\circ)}&:(x,y)\stackrel{r}{\mapsto}(y,-x)\\[3pt]r_{(O,270^\circ)}&:(x,y)\stackrel{r}{\mapsto}(y,-x)\end{align}|| |
||\begin{align}r^{-1}_{(O,90^\circ)}&=r_{(O,-90^\circ)}\\[3pt]r^{-1}_{(O,-270^\circ)}&=r_{(O,270^\circ)}\\[3pt]r^{-1}_{(O,180^\circ)}&=r_{(O,180^\circ)}\\[3pt]r^{-1}_{(O,-90^\circ)}&=r_{(O,90^\circ)}\\[3pt]r^{-1}_{(O,270^\circ)}&=r_{(O,-270^\circ)}\end{align}|| |
|
Reflection (Symmetry) |
||\begin{align}s_x&:(x,y)\stackrel{s}{\mapsto}(x,-y)\\[3pt]s_y&:(x,y)\stackrel{s}{\mapsto}(-x,y)\\[3pt]s_{\small/}&:(x,y)\stackrel{s}{\mapsto}(y,x)\\[3pt]s_{\tiny\backslash}&:(x,y)\stackrel{s}{\mapsto}(-y,-x)\end{align}|| |
||\begin{align}s^{-1}_x&=s_x\\[3pt]s^{-1}_y&=s_y\\[3pt]s^{-1}_{\small/}&=s_{\small/}\\[3pt]s^{-1}_{\tiny\backslash}&=s_{\tiny\backslash}\end{align}|| |
|
Dilation |
||h_{(O,k)}:(x,y)\stackrel{h}{\mapsto}(kx,ky)|| |
||h^{-1}_{(O,k)}=h_{\left(\frac{1}{k},\frac{1}{k}\right)}:(x,y)\stackrel{h}{\mapsto}\left(\dfrac{x}{k},\dfrac{y}{k}\right)|| |
|
Conic |
Standard equations |
Parameters |
|---|---|---|
|
Circle Geometric locus of all points located at an equal distance from the centre. |
||x^2+y^2=r^2|| ||(x-h)^2+(y-k)^2=r^2|| |
|r:| radius |(h,k):| Centre of circle |
|
Ellipse Geometric locus of all points for which the sum of the distances to the two foci is constant. |
||\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1|| ||\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1|| |
||\begin{align}a&=\dfrac{\text{Horizontal axis}}{2}\\b&=\dfrac{\text{Vertical Axis}}{2}\end{align}|| |(h,k):| Centre of the ellipse |
|
Hyperbola Geometric locus of all points for which the absolute value of the difference in distance to the two foci is constant. |
||\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=\pm1|| ||\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=\pm1|| |
Asymptotes: ||\begin{align}y&=\dfrac{b}{a}(x-h)+k\\y&=-\dfrac{b}{a}(x-h)+k\end{align}|| |(h,k):| Centre of the hyperbola |
|
Parabola Geometric locus of all points located at an equal distance from the directrix and the focal point. |
||(x-h)^2=4c(y-k)|| ||(y-k)^2=4c(x-h)|| |
||\vert c\vert :\dfrac{\text{Distance focus-directrix}}{2}|| |(h,k):| Vertex of the parabola |
||P(\theta)=(\cos\theta,\sin\theta)||
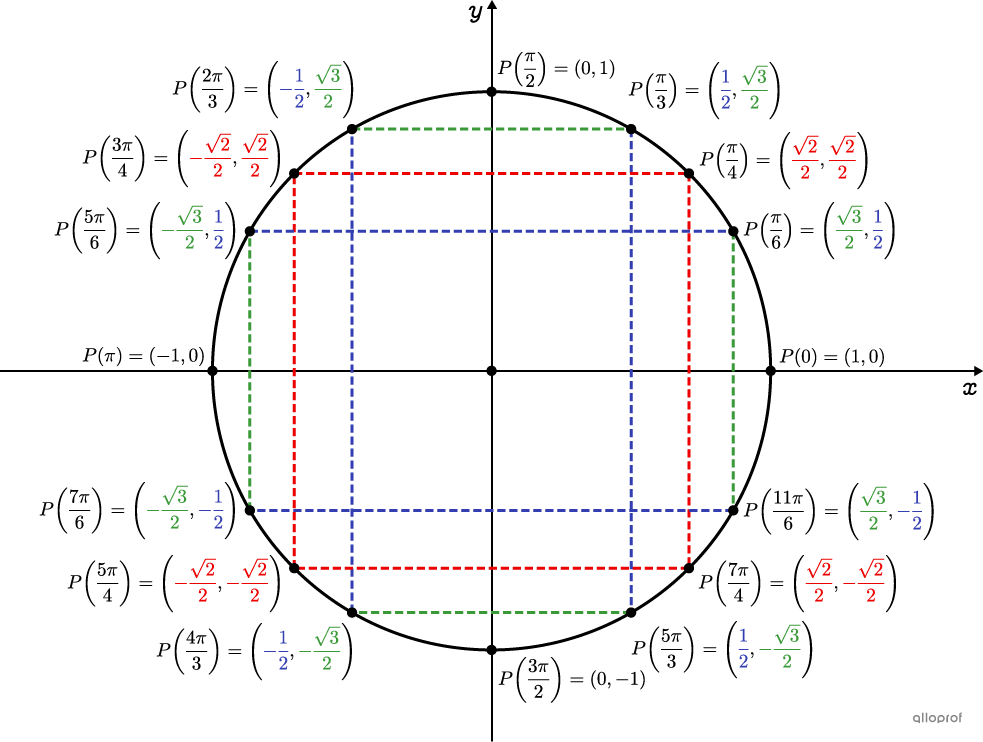
|
Concept |
Formulas |
|---|---|
|
Probability |
||\text{Probability}=\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}}|| |
|
Complementary probability |
||\mathbb{P}(A')=1-P(A)|| |
|
Probability of mutually exclusive events |
||\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)|| |
|
Probability of non-mutually exclusive events |
||\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\cap B)|| |
|
Conditional probability |
||\mathbb{P}(B\mid A)=\mathbb{P}_A(B)=\dfrac{\mathbb{P}(B\cap A)}{\mathbb{P}(A)}|| |
|
Expected gain |
||\mathbb{E}[\text{Gain}]=\text{Probability of winning}\times\text{Net gain}+\text{Probability of losing}\times\text{Net loss}|| |
|
Mathematical expectation |
||\mathbb{E}[X]=x_1\mathbb{P}(x_1)+x_2\mathbb{P}(x_2)+\ldots+x_n\mathbb{P}(x_n)||where the possible outcomes of |X| are the values |x_1, \ldots, x_n.| |
|
Measure |
Listed data |
Condensed data |
Grouped data |
|---|---|---|---|
|
Mean |
||\overline{x}=\dfrac{\sum x_i}{n}|| |
||\overline{x}=\dfrac{\sum x_i n_i}{n}|| |
Approximate mean: ||\overline{x}=\dfrac{\sum m_i n_i}{n}|| |
|
Median |
||\text{Rank}_\text{median}=\left(\dfrac{n+1}{2}\right)|| If |n| is odd, the median is obtained directly. If |n| is even, the median is obtained by calculating the mean of the two central data values. |
||\text{Rank}_\text{median}=\left(\dfrac{n+1}{2}\right)|| If |n| is odd, the median is obtained directly. If |n| is even, the median is obtained by calculating the mean of the two central data values. |
Medial class: The class that contains the median. The median of a grouped-data distribution is often estimated by calculating the middle of the medial class. |
|
Mode |
The most frequent data value |
The most frequent data value |
Modal class: The class with the largest frequency |
|
Measure |
Listed data |
Condensed data |
Grouped data |
|---|---|---|---|
|
Range |
||R=x_\text{max}-x_\text{min}|| |
||R=\text{Value}_\text{Max}-\text{Value}_\text{Min}|| |
||R=\text{Boundary}_\text{upper}-\text{Boundary}_\text{lower}|| |
|
Interquartile range |
||IR=Q_3-Q_1|| |
||IR=Q_3-Q_1|| |
||IR=Q_3-Q_1|| |
|
Quarter range |
||Q=\dfrac{EI}{2}=\dfrac{Q_3-Q_1}{2}|| |
||Q=\dfrac{EI}{2}=\dfrac{Q_3-Q_1}{2}|| |
||Q=\dfrac{EI}{2}=\dfrac{Q_3-Q_1}{2}|| |
|
Mean deviation |
||MD=\dfrac{\sum\mid x_i-\overline{x}\mid}{n}|| |
||MD=\dfrac{\sum n_i\mid X_i-\overline{x}\mid}{n}|| |
||MD=\dfrac{\sum n_i \mid m_i-\overline{x}\mid}{n}|| |
|
Standard deviation |
||\sigma=\sqrt{\dfrac{\sum (x_i-\overline{x})^2}{n}}|| |
||\sigma=\sqrt{\dfrac{\sum n_i(X_i-\overline{x})^2}{n}}|| |
||\sigma=\sqrt{\dfrac{\sum n_i (m_i-\overline{x})^2}{n}}|| |
|
Measure |
Formulas |
|---|---|
|
Quintile rank |
||R_5(x)\approx\left(\dfrac{\text{No. of data values greater than } x+\dfrac{\text{No. of data values equal to }x}{2}}{\text{Total number of data values}}\right) \times 5|| If the result is not a whole number, round up. |
|
Percentile rank |
||R_{100}(x)\approx\left(\dfrac{\text{No. of data values less than } x+\dfrac{\text{No. of data values equal to }x}{2}}{\text{Total number of data values}}\right) \times 100|| If the result is not a whole number, round up to the next whole number, unless the result is |99.| |
|
Calculating the correlation coefficient on the Cartesian plane |
|
|---|---|
|
||r\approx\pm\left(1-\dfrac{l}{L}\right)|| where |L| represents the length and |l,| the width of the rectangle that encompasses the scatter plot. The sign of |r| depends on the direction of the scatter plot. |
|
|
Interpretation of the correlation coefficient |
|
| Close to |0| | Zero link between the variables |
| Close to |\text{-}0.5| or |0.5| | Weak link between the variables |
| Close to |\text{-}0.75| or |0.75| | Moderate link between the variables |
| Close to |\text{-}0.87| or |0.87| | Strong link between the variables |
| Equal to |\text{-}1| or |1| | Perfect link between the variables |