|
Arithmétique et algèbre |
Géométrie | Géométrie analytique | Probabilités et statistique |
|---|---|---|---|
|
Exprimer un nombre en pourcentage Les fonctions exponentielles et logarithmiques |
La conversion des unités de mesure Le périmètre et l'aire de figures planes Les mesures dans les polygones L'aire et le volume des solides Les mesures dans les triangles rectangles |
Les droites dans le plan cartésien |
|
||\dfrac{\text{numérateur}}{\text{dénominateur}}\times100|| |
||\dfrac{\text{numérateur}}{\text{dénominateur}}=\dfrac{\text{nombre recherché}}{100}|| |
|
Propriétés |
Addition |
Multiplication |
|---|---|---|
|
||a+b=b+a|| |
||a\times b=b\times a|| |
|
||(a+b)+c=a+(b+c)|| |
||(a\times b)\times c=a\times(b\times c)|| |
|
||a+0=0+a=a|| |
||a\times1=1\times a=a|| |
|
|
||a\times0=0\times a=0|| |
|
||a+-a=-a+a=0|| |
||a\times\dfrac{1}{a}=1|| |
|
||a\times(b\pm c)=a\times b\pm a\times c|| |
|
|
Fonctions |
Règles de base |
Règles transformées |
||
|---|---|---|---|---|
|
Degré 0 |
||y=b|| |
|
||
|
Degré 1 |
||y=x|| |
Forme |
Forme |
Forme |
|
||y=ax+b|||a| : taux de variation |b| : ordonnée à l'origine||a=\dfrac{y_2-y_1}{x_2-x_1}|| |
||\dfrac{x}{a}+\dfrac{y}{b}=1|||a| : abscisse à l'origine |b| : ordonnée à l'origine |
||Ax+By+C=0|| |
||
|
|\Rightarrow| symétrique||\begin{align}a_s&=\dfrac{-b_f}{a_f}\\b_s&=b_f\end{align}|| |
|\Rightarrow| fonctionnelle||\begin{align}a_f&=\dfrac{-b_s}{a_s}\\b_f&=b_s\end{align}|| |
|\Rightarrow| fonctionnelle||\begin{align}a_f&=\dfrac{-A}{B}\\b_f&=\dfrac{-C}{B}\end{align}|| |
||
|
|\Rightarrow| générale Dénominateur commun et mettre tout du même côté |
|\Rightarrow| générale Dénominateur commun et mettre tout du même côté |
|\Rightarrow| symétrique||\begin{align}a_s&=\dfrac{-C}{A}\\\\b_s&=\dfrac{-C}{B}\end{align}|| |
||
|
Degré 2 |
||y=x^2|| |
Forme |
Forme |
Forme |
|
||y=ax^2+bx+c|| |
||\begin{align}y&=\text{a}\big(b(x-h)\big)^2+k\\y&=\text{a }b^2(x-h)^2+k\\y&=a(x-h)^2+k\end{align}|| |
Deux zéros||y=a(x-z_1)(x-z_2)||Un seul zéro||y=a(x-z_1)^2|| |
||
|
Nombre de zéros||\sqrt{b^2-4ac}|| |
Nombre de zéros||\sqrt{\dfrac{-k}{a}}|| |
Nombre de zéros |
||
|
Valeur des zéros||\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}|| |
Valeur des zéros||h\pm\sqrt{\dfrac{-k}{a}}|| |
Valeur des zéros |z_1| et |z_2| |
||
|
Valeur absolue |
||y=\vert x\vert|| |
Forme canonique |
||
|
||\begin{align}y&=\text{a }\vert b(x-h)\vert+k\\y&=\text{a }\vert b\vert\times\vert x-h\vert+k\\y&=a\ \vert x-h\vert+k\end{align}|| |
||||
|
Racine carrée |
||y=\sqrt{x}|| |
Forme canonique |
||
|
||\begin{align}y&=\text{a}\sqrt{b(x-h)}+k\\[3pt]y&=\text{a}\sqrt b\sqrt{\pm(x-h)}+k\\[3pt]y&=a\sqrt{\pm(x-h)}+k\end{align}|| |
||||
| Partie entière | ||y=[x]|| | Forme canonique | ||
| ||y=a\big[b\,(x-h)\big]+k|| | ||||
|
Fonctions |
Règles de base |
Règles transformées |
Définitions et lois |
|---|---|---|---|
|
Exponentielle |
||f(x)=c^x|| |
||f(x)=a(c)^{b(x-h)}+k|| |
||\begin{align}a^0&=1\\[3pt]a^1&=a\\[3pt]a^{-m}&=\dfrac{1}{a^m}\\[3pt]a^{^{\frac{\large{m}}{\large{n}}}}&=\sqrt[\large{n}]{a^m}\\[3pt]a^m=a^n&\!\!\ \Leftrightarrow\ m=n\\[3pt]a^ma^n&=a^{m+n}\\[3pt]\dfrac{a^m}{a^n}&=a^{m-n}\\[3pt](ab)^m&=a^mb^m\\[3pt](a^m)^{^{\Large{n}}}&=a^{mn}\\[3pt]\left(\dfrac{a}{b}\right)^m&=\dfrac{a^m}{b^m}\\[3pt]\sqrt[\large{n}]{ab}&=\sqrt[\large{n}]{a}\ \sqrt[\large{n}]{b}\\[3pt]\sqrt[\large{n}]{\dfrac{a}{b}}&=\dfrac{\sqrt[\large{n}]{a}}{\sqrt[\large{n}]{b}}\end{align}|| |
|
Logarithme |
||f(x)=\log_cx|| |
||f(x)=a\log_c(b(x-h))+k|| |
||\begin{align}\log_c1&=0\\[3pt]\log_cc&=1\\[3pt]c^{\log_{\large{c}}m}&=m\\[3pt]\log_cc^m&=m\\[3pt]\log_cm=\log_cn\ &\Leftrightarrow\ m=n\\[3pt]\log_c(mn)&=\log_cm+\log_cn\\[3pt]\log_c\left(\dfrac{m}{n}\right)&=\log_cm-\log_cn\\[3pt]\log_c(m^n)&=n\log_cm\\[3pt]\log_cm&=\dfrac{\log_sm}{\log_sc}\end{align}|| |
|
L'une est la réciproque de l'autre||x=c^y\ \Longleftrightarrow\ y=\log_cx|| |
|||
|
Fonctions |
Règles de base |
Règles transformées |
Particularités |
|---|---|---|---|
|
Sinus |
||f(x)=\sin x|| |
||f(x)=a\sin\big(b(x-h)\big)+k|| |
||\begin{align}\vert a\vert&=\dfrac{\max-\min}{2}\\[3pt]\vert b \vert&=\dfrac{2\pi}{\text{période}}\\[3pt]\text{Ima}f&=[k-a,k+a]\end{align}||Zéros : Une infinité de la forme |(x_1+nP)| et |(x_2+nP)| où |x_1| et |x_2| sont des zéros consécutifs, |n\in\mathbb{Z}| et |P| est la période. |
|
Cosinus |
||f(x)=\cos x|| |
||f(x)=a\cos\big(b(x-h)\big)+k|| |
|
|
Tangente |
||f(x)=\tan x|| |
||f(x)=a\tan\big(b(x-h)\big)+k|| |
||\vert b\vert=\dfrac{\pi}{\text{période}}\\[3pt]\text{Dom}\ f=\mathbb{R}\backslash\left\{\left(h+\dfrac{P}{2}\right)+nP\right\}||où |n\in\mathbb{Z}| et |P| est la période. Zéros : Une infinité de la forme |x_1+nP| où |x_1| est un zéro, |n\in \mathbb{Z}| et |P| est la période. |
|
Arc sinus |
||f(x)=\arcsin(x)||ou||f(x)=\sin^{-1}(x)|| |
||f(x)=a\arcsin\big(b(x-h)\big)+k|| |
|
|
Arc cosinus |
||f(x)=\arccos(x)||ou||f(x)=\cos^{-1}(x)|| |
||f(x)=a\arccos\big(b(x-h)\big)+k|| |
|
|
Arc tangente |
||f(x)=\arctan(x)||ou||f(x)=\tan^{-1}(x)|| |
||f(x)=a\arctan\big(b(x-h)\big)+k|| |
|
|
Identités de base |
|||||
|---|---|---|---|---|---|
|
||\sin^2\theta+\cos^2\theta=1|| |
||1+\tan^2\theta=sec^2\theta|| |
||1+\text{cotan}^2\theta=\text{cosec}^2\theta|| |
|||
|
Autres identités |
|||||
|
||\begin{align}\sin(a+b)&=\sin a\cos b+\cos a\sin b\\[3pt]\sin(a-b)&=\sin a\cos b-\cos a\sin b\\[3pt]\cos(a+b)&=\cos a\cos b-\sin a\sin b\\[3pt]\cos(a-b)&=\cos a\cos b+\sin a\sin b\\[3pt]\tan(a+b)&=\dfrac{\tan a+\tan b}{1-\tan a\tan b}\\[3pt]\tan(a-b)&=\dfrac{\tan a-\tan b}{1+\tan a\tan b}\end{align}|| |
||\begin{align}\sin2x&=2\sin x\cos x\\[3pt]\cos2x&=1-2\sin^2x\\[3pt]\tan2x&=\dfrac{2}{\text{cotan}x-\tan x}\\[3pt]\sin(-\theta)&=-\sin\theta\\[3pt]\cos(-\theta)&=\cos\theta\\[3pt]\sin\left(\theta+\dfrac{\pi}{2}\right)&=\cos\theta\\[3pt]\cos\left(\theta+\dfrac{\pi}{2}\right)&=-\sin\theta\end{align}|| |
||||
| |\text{km}| | |\text{hm}| | |\text{dam}| | |\text{m}| | |\text{dm}| | |\text{cm}| | |\text{mm}| |
| Dans ce sens |\Rightarrow \times 10\qquad \qquad\qquad| Dans ce sens |\Leftarrow \div 10| | ||||||
| |\text{km}^2| | |\text{hm}^2| | |\text{dam}^2| | |\text{m}^2| | |\text{dm}^2| | |\text{cm}^2| | |\text{mm}^2| |
| Dans ce sens |\Rightarrow \times 100\qquad \qquad\qquad| Dans ce sens |\Leftarrow \div 100| | ||||||
| |\text{km}^3| | |\text{hm}^3| | |\text{dam}^3| | |\text{m}^3| | |\text{dm}^3| | |\text{cm}^3| | |\text{mm}^3| |
| Dans ce sens |\Rightarrow \times 1000\qquad \qquad\qquad| Dans ce sens |\Leftarrow \div 1000| | ||||||
|
Figures |
Périmètre |
Aire |
|
|---|---|---|---|
|
Triangle |
La somme de tous les côtés |
|A =\dfrac{b\times h}{2}| |
|
|
Carré |
|P=4 \times c| |
|\begin{align} A &= c \times c\\ |
|
|
Rectangle |
|\begin{align} P &= b+h+b+h\\ |
|A=bh| |
|
|
Losange |
|P=4 \times c| |
|A=\dfrac{D\times d}{2}| |
|
|
Parallélogramme |
La somme de tous les côtés |
|A=bh| |
|
|
Trapèze |
La somme de tous les côtés |
|A=\dfrac{(B+b)\times h}{2}| |
|
|
Polygone régulier |
|P=n \times c| |
|A=\dfrac{can}{2}|
|
|
|
Polygones quelconque |
La somme de tous les côtés |
Décomposer le polygone en plusieurs polygones connus et additionner les aires de ces polygones. |
|
|
Disque et cercle |
|\begin{align} d &= 2r\\\\ |
\begin{align} C &= \pi d\\\\ |
|A=\pi r^2| |
|
Arc de cercle et secteur de disque |
|\displaystyle \frac{\text{Angle au centre}}{360^o}=\frac{\text{Mesure d'arc}}{2\pi r}| |
|\displaystyle \frac{\text{Angle au centre}}{360^o}=\frac{\text{Aire du secteur}}{\pi r^2}| |
|
|
Les théorèmes dans le cercle |
|---|
|
Les théorèmes en lien avec les rayons, les diamètres, les cordes et les arcs :
Les théorèmes en lien avec les angles :
Les théorèmes en lien avec les sécantes et les tangentes au cercle :
|
|
Nombre total de diagonales |
Nombre de diagonales à chaque sommet |
Somme des mesures des angles intérieurs |
Mesure d'un angle intérieur |
|---|---|---|---|
|
|\dfrac{n(n-3)}{2}| |
|n-3| |
|180(n-2)| |
|\dfrac{180(n-2)}{n}| |
|
Solides |
Aire latérale |
Aire totale |
Volume |
|---|---|---|---|
|
Prisme et cylindre |
Somme des aires des faces latérales du solide |A_L=P_b\times h| |
Somme des aires de toutes les faces du solide |A_T = A_L+2A_b| |
|V=A_b\times h| |
|
Pyramide et cône |
Somme des aires des faces latérales du solide |A_L=\displaystyle \frac{P_b\times a}{2}| |
Somme des aires de toutes les faces du solide |A_T = A_L+A_b| |
|V=\displaystyle \frac{A_b\times h}{3}| |
|
Sphère et boule |
|A=4\pi r^2| |
|V=\displaystyle \frac{4\pi r^3}{3}| |
|
|
Les théorèmes dans le triangle rectangle |
|---|
|
|
Les relations métriques dans le triangle rectangle |
|
Théorème de la hauteur relative à l'hypoténuse Dans tout triangle rectangle, la hauteur |(h)| issue du sommet de l'angle droit est moyenne proportionnelle entre les mesures des deux segments |(m| et |n)| qu'elle détermine sur l'hypoténuse.||\dfrac{m}{h}=\dfrac{h}{n}\quad\text{ou}\quad h^2=mn||Théorème du produit des cathètes Dans tout triangle rectangle, le produit des cathètes |(a| et |b)| est égal au produit de l'hypoténuse |(c)| et de sa hauteur relative |(h)|.||ch=ab\quad\text{ou}\quad h=\dfrac{ab}{c}||Théorème de la cathète Dans tout triangle rectangle, chaque cathète |(a| ou |b)| est moyenne proportionnelle entre la longueur de sa projection sur l'hypoténuse (respectivement |m| et |n|) et l'hypoténuse entière |(c).|||\dfrac{m}{a}=\dfrac{a}{c}\quad\text{ou}\quad a^2=mc\\\dfrac{n}{c}=\dfrac{b}{c}\quad\text{ou}\quad b^2=nc|| |
|
Rapports trigonométriques |
Lois trigonométriques (triangles quelconques) |
|
|---|---|---|
| ||\sin A=\dfrac{\text{Opposé}}{\text{Hypoténuse}}|| | ||\text{cosec }A=\dfrac{1}{\sin A}=\dfrac{\text{Hypoténuse}}{\text{Opposé}}|| | ||\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}|| |
| ||\cos A=\dfrac{\text{Adjacent}}{\text{Hypoténuse}}|| | ||\text{sec }A=\dfrac{1}{\cos A}=\dfrac{\text{Hypoténuse}}{\text{Adjacent}}|| | ||\begin{align}a^2&=b^2+c^2-2bc\cos A\\[3pt]b^2&=a^2+c^2-2ac\cos B\\[3pt]c^2&=a^2+b^2-2ab\cos C\end{align}|| |
| ||\tan A=\dfrac{\text{Opposé}}{\text{Adjacent}}|| | ||\text{cotan}A=\dfrac{1}{\tan A}=\dfrac{\text{Adjacent}}{\text{Opposé}}|| | |
|
Rapport de similitude |
Rapport d'aires |
Rapport de volumes |
|---|---|---|
|
||k=\dfrac{\text{Longueur figure image}}{\text{Longueur figure initiale}}|| |
||k^2=\dfrac{\text{Aire figure image}}{\text{Aire figure initiale}}|| |
||k^3=\dfrac{\text{Volume solide image}}{\text{Volume solide initiale}}|| |
|
Composantes |\boldsymbol{(a,b)}| d'un vecteur |
|||
|---|---|---|---|
|
||a=\Vert \overrightarrow{u}\Vert \cos \theta|| ||b=\Vert \overrightarrow{u}\Vert \sin \theta|| |
Soit le vecteur |\overrightarrow{AB}| avec |A(x_1, y_1)| et |B(x_2, y_2)| |
||
|
Norme d'un vecteur |
|||
|
Soit le vecteur |\overrightarrow{u}=(a,b)| |
Soit le vecteur |\overrightarrow{AB}| avec |A(x_1, y_1)| et |B(x_2, y_2)| |
||
|
Orientation d'un vecteur |
|||
|
|\theta=\tan^{-1}\left(\displaystyle\frac{b}{a}\right)| |
|
||
|
Somme de deux vecteurs |
|||
|
Soit |\overrightarrow{u}=(a,b)| et |\overrightarrow{v}=(c,d)| |
|\Vert \overrightarrow{u}+\overrightarrow{v}\Vert=\Vert \overrightarrow{u}\Vert+\Vert \overrightarrow{v}\Vert-2\Vert \overrightarrow{u}\Vert\ \Vert \overrightarrow{v}\Vert\ \cos\theta| |
||
|
Soustraction de deux vecteurs |
|||
|
Soit |\overrightarrow{u}=(a,b)| et |\overrightarrow{v}=(c,d)| |
|\Vert \overrightarrow{u}+\overrightarrow{v}\Vert=\Vert \overrightarrow{u}\Vert+\Vert \overrightarrow{v}\Vert-2\Vert \overrightarrow{u}\Vert\ \Vert \overrightarrow{v}\Vert\ \cos\theta| |
||
|
Multiplication par un scalaire |
|||
|
Soit |k| un scalaire et |\overrightarrow{u}=(a,b)| |
|||
|
Produit scalaire |
|||
|
Si le produit scalaire est de |0|, alors les vecteurs sont perpendiculaires. |
|||
|
À l'aide des composantes |
À l'aide de la norme et de l'orientation |
||
|
Propriétés de l'addition de deux vecteurs |
|||
|
1) La somme de deux vecteurs est un vecteur. |
|
||
|
2) Commutativité |
|\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u}| |
||
|
3) Associativité |
|(\overrightarrow{u} + \overrightarrow{v}) + \overrightarrow{w} = \overrightarrow{u} + (\overrightarrow{v} + \overrightarrow{w})| |
||
|
4) Existence d'un élément neutre |
|\overrightarrow{u}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{u}=\overrightarrow{u}| |
||
|
5) Existence d'opposés |
|\overrightarrow{u}+(-\overrightarrow{u})=-\overrightarrow{u}+\overrightarrow{u}=\overrightarrow{0}| |
||
|
Propriétés de la multiplication par un scalaire |
|||
|
1) Le produit d'un vecteur par un scalaire est toujours un vecteur. |
|
||
|
2) Associativité |
|k_1(k_2\overrightarrow{u})=(k_1k_2)\overrightarrow{u}| |
||
|
3) Existence d'un élément neutre |
|1\times \overrightarrow{u}=\overrightarrow{u}\times 1=\overrightarrow{u}| |
||
|
4) Distributivité sur l'addition de vecteurs |
|k(\overrightarrow{u}+\overrightarrow{v})=k\overrightarrow{u}+k\overrightarrow{v}| |
||
|
5) Distributivité sur l'addition de scalaires |
|(k_1+k_2)\overrightarrow{u}=k_1\overrightarrow{u}+k_2\overrightarrow{v}| |
||
|
Propriétés du produit scalaire |
|||
|
1) Commutativité |
|\overrightarrow{u}\cdot \overrightarrow{v}=\overrightarrow{v}\cdot \overrightarrow{u}| |
||
|
2) Associativité des scalaires |
|k_1\overrightarrow{u}\cdot k_2\overrightarrow{v}=k_1k_2(\overrightarrow{u}\cdot\overrightarrow{v})| |
||
|
3) Distributivité sur une somme vectorielle |
|\overrightarrow{u}\cdot(\overrightarrow{v}+\overrightarrow{w})=(\overrightarrow{u}\cdot\overrightarrow{v})+(\overrightarrow{u}\cdot\overrightarrow{w})| |
||
|
Concepts |
Formules |
|||||
|---|---|---|---|---|---|---|
|
Accroissements |
||\begin{align}\Delta x&=x_2-x_1\\[3pt]\Delta y&=y_2-y_1\end{align}|| |
|||||
|
Distance entre deux points |
||d(A,B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}|| |
|||||
|
Coordonnées du point de partage |
Rapport partie |
Rapport partie |
||||
|
||\begin{align}x_p&=x_1+\dfrac{r}{s}(x_2-x_1)\\[3pt]y_p&=y_1+\dfrac{r}{s}(y_2-y_1)\end{align}|| |
||\begin{align}x_p&=x_1+\dfrac{r}{r+s}(x_2-x_1)\\[3pt]y_p&=y_1+\dfrac{r}{r+s}(y_2-y_1)\end{align}|| |
|||||
|
Coordonnées du point milieu |
||(x_m,y_m)=\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)|| |
|||||
|
Pente d'une droite |
||a=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}|| |
|||||
|
Comparaison de deux droites d'équations |y=ax+b| |
Parallèles |
Parallèles |
Perpendiculaires |
|||
|
||\begin{align}a_1&=a_2\\[3pt]b_1&=b_2\end{align}|| |
||\begin{align}a_1&=a_2\\[3pt]b_1&\neq b_2\end{align}|| |
||a_1=-\dfrac{1}{a_2}|| |
||||
|
Transformations |
Règles |
Réciproques |
|---|---|---|
|
Translation |
||t_{(a,b)}:(x,y)\stackrel{t}{\mapsto}(x+a,y+b)|| |
||t^{-1}_{(a,b)}=t_{(-a,-b)}:(x,y)\stackrel{t}{\mapsto}(x-a,y-b)|| |
|
Rotation |
||\begin{align}r_{(O,90^\circ)}&:(x,y)\stackrel{r}{\mapsto}(-y,x)\\[3pt]r_{(O,-270^\circ)}&:(x,y)\stackrel{r}{\mapsto}(-y,x)\\[3pt]r_{(O,180^\circ)}&:(x,y)\stackrel{r}{\mapsto}(-x,-y)\\[3pt]r_{(O,-90^\circ)}&:(x,y)\stackrel{r}{\mapsto}(y,-x)\\[3pt]r_{(O,270^\circ)}&:(x,y)\stackrel{r}{\mapsto}(y,-x)\end{align}|| |
||\begin{align}r^{-1}_{(O,90^\circ)}&=r_{(O,-90^\circ)}\\[3pt]r^{-1}_{(O,-270^\circ)}&=r_{(O,270^\circ)}\\[3pt]r^{-1}_{(O,180^\circ)}&=r_{(O,180^\circ)}\\[3pt]r^{-1}_{(O,-90^\circ)}&=r_{(O,90^\circ)}\\[3pt]r^{-1}_{(O,270^\circ)}&=r_{(O,-270^\circ)}\end{align}|| |
|
Réflexion (Symétrie) |
||\begin{align}s_x&:(x,y)\stackrel{s}{\mapsto}(x,-y)\\[3pt]s_y&:(x,y)\stackrel{s}{\mapsto}(-x,y)\\[3pt]s_{\small/}&:(x,y)\stackrel{s}{\mapsto}(y,x)\\[3pt]s_{\tiny\backslash}&:(x,y)\stackrel{s}{\mapsto}(-y,-x)\end{align}|| |
||\begin{align}s^{-1}_x&=s_x\\[3pt]s^{-1}_y&=s_y\\[3pt]s^{-1}_{\small/}&=s_{\small/}\\[3pt]s^{-1}_{\tiny\backslash}&=s_{\tiny\backslash}\end{align}|| |
|
Homothétie |
||h_{(O,k)}:(x,y)\stackrel{h}{\mapsto}(kx,ky)|| |
||h^{-1}_{(O,k)}=h_{\left(\frac{1}{k},\frac{1}{k}\right)}:(x,y)\stackrel{h}{\mapsto}\left(\dfrac{x}{k},\dfrac{y}{k}\right)|| |
|
Coniques |
Équations canoniques |
Paramètres |
|---|---|---|
|
Cercle Lieu géométrique de tous les points situés à égale distance du centre. |
||x^2+y^2=r^2|| ||(x-h)^2+(y-k)^2=r^2|| |
|r:| rayon |(h,k):| Centre du cercle |
|
Ellipse Lieu géométrique de tous les points dont la somme des distances aux deux foyers est constante. |
||\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1|| ||\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1|| |
||\begin{align}a&=\dfrac{\text{Axe horizontale}}{2}\\b&=\dfrac{\text{Axe verticale}}{2}\end{align}|| |(h,k):| Centre de l'ellipse |
|
Hyperbole Lieu géométrique de tous les points dont la valeur absolue de la différence de la distance aux foyers est constante. |
||\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=\pm1|| ||\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=\pm1|| |
Asymptotes : ||\begin{align}y&=\dfrac{b}{a}(x-h)+k\\y&=-\dfrac{b}{a}(x-h)+k\end{align}|| |(h,k):| Centre de l'hyperbole |
|
Parabole Lieu géométrique de tous les points situés à égale distance de la directrice et du foyer |
||(x-h)^2=4c(y-k)|| ||(y-k)^2=4c(x-h)|| |
||\vert c\vert :\dfrac{\text{Distance foyer-directrice}}{2}|| |(h,k):| Sommet de la parabole |
||P(\theta)=(\cos\theta,\sin\theta)||
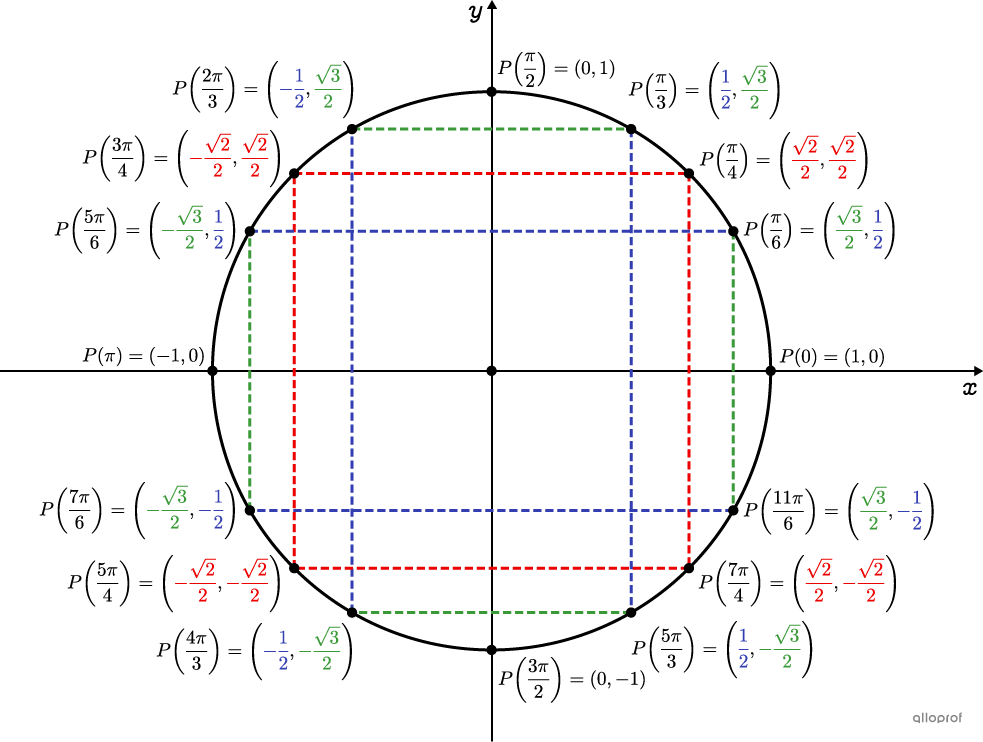
|
Concepts |
Formules |
|---|---|
|
Probabilité |
||\text{Probabilité}=\dfrac{\text{Nbr de cas favorables}}{\text{Nbr de cas possibles}}|| |
|
Probabilité complémentaire |
||\mathbb{P}(A')=1-P(A)|| |
|
Probabilité d'événements mutuellement exclusifs |
||\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)|| |
|
Probabilité d'événements non mutuellement exclusifs |
||\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\cap B)|| |
|
Probabilité conditionnelle |
||\mathbb{P}(B\mid A)=\mathbb{P}_A(B)=\dfrac{\mathbb{P}(B\cap A)}{\mathbb{P}(A)}|| |
|
Espérance de gain |
||\mathbb{E}[\text{Gain}]=\text{Probabilité de gagner}\times\text{Gain net}+\text{Probabilité de perdre}\times\text{Perte nette}|| |
|
Espérance mathématique |
||\mathbb{E[X]}=x_1\mathbb{P}(x_1)+x_2\mathbb{P}(x_2)+\ldots+x_n\mathbb{P}(x_n)||où les résultats possibles de |X| sont les valeurs |x_1, \ldots, x_n.| |
|
Mesures |
Données non regroupées |
Données condensées |
Données regroupées |
|---|---|---|---|
|
Moyenne |
||\overline{x}=\dfrac{\sum x_i}{n}|| |
||\overline{x}=\dfrac{\sum x_i n_i}{n}|| |
||\overline{x}=\dfrac{\sum m_i n_i}{n}|| |
|
Médiane |
||\text{Rang}_\text{médiane}=\left(\dfrac{n+1}{2}\right)||Si |n| est impair, on obtient directement la médiane. Si |n| est pair, on obtient la médiane en faisant la moyenne des deux données centrales. |
||\text{Rang}_\text{médiane}=\left(\dfrac{n+1}{2}\right)||Si |n| est impair, on obtient directement la médiane. Si |n| est pair, on obtient la médiane en faisant la moyenne des deux données centrales. |
Classe médiane : La classe contenant la médiane. On estime souvent la médiane d'une distribution à données regroupées en calculant le milieu de la classe médiane. |
|
Mode |
La donnée la plus fréquente |
La valeur avec le plus grand effectif |
Classe modale : La classe ayant le plus grand effectif |
|
Mesures |
Données non regroupées |
Données condensées |
Données regroupées |
|---|---|---|---|
|
Étendue |
||E=x_\text{max}-x_\text{min}|| |
||E=\text{Valeur}_\text{Max}-\text{Valeur}_\text{Min}|| |
||E=\text{Borne}_\text{sup}-\text{Borne}_\text{inf}|| |
|
Étendue Interquartile |
||EI=Q_3-Q_1|| |
||EI=Q_3-Q_1|| |
||EI=Q_3-Q_1|| |
|
Intervalle semi-interquartile |
||Q=\dfrac{EI}{2}=\dfrac{Q_3-Q_1}{2}|| |
||Q=\dfrac{EI}{2}=\dfrac{Q_3-Q_1}{2}|| |
||Q=\dfrac{EI}{2}=\dfrac{Q_3-Q_1}{2}|| |
|
Écart moyen |
||EM=\dfrac{\sum\mid x_i-\overline{x}\mid}{n}|| |
||EM=\dfrac{\sum n_i\mid X_i-\overline{x}\mid}{n}|| |
||EM=\dfrac{\sum n_i \mid m_i-\overline{x}\mid}{n}|| |
|
Écart type |
||\sigma=\sqrt{\dfrac{\sum (x_i-\overline{x})^2}{n}}|| |
||\sigma=\sqrt{\dfrac{\sum n_i(X_i-\overline{x})^2}{n}}|| |
||\sigma=\sqrt{\dfrac{\sum n_i (m_i-\overline{x})^2}{n}}|| |
|
Mesures |
Formules |
|---|---|
|
Rang cinquième |
||R_5(x)\approx\left(\dfrac{\text{Nbre de données supérieures à } x+\dfrac{\text{Nbre de données égales à }x}{2}}{\text{Nbre total de données}}\right) \times 5||Si le résultat n'est pas un nombre entier, on arrondit à l'entier supérieur. |
|
Rang centile |
||R_{100}(x)\approx\left(\dfrac{\text{Nbre de données inférieures à } x+\dfrac{\text{Nbre de données égales à }x}{2}}{\text{Nbre total de données}}\right) \times 100||Si le résultat n'est pas un nombre entier, on arrondit à l'entier supérieur, sauf si celui-ci est |99.| |
|
Calcul du coefficient de corrélation dans le plan cartésien |
|
|---|---|
|
||r\approx\pm\left(1-\dfrac{l}{L}\right)||où |L| représente la longueur et |l,| la largeur du rectangle englobant le nuage de points. Le signe de |r| dépend du sens du nuage de points. |
|
|
Interprétation du coefficient de corrélation |
|
| Près de |0| | Lien nul entre les variables |
| Près de |\text{-}0{,}5| ou de |0{,}5| | Lien faible entre les variables |
| Près de |\text{-}0{,}75| ou de |0{,}75| | Lien moyen entre les variables |
| Près de |\text{-}0{,}87| ou de |0{,}87| | Lien fort entre les variables |
| Égal à |\text{-}1| ou à |1| | Lien parfait entre les variables |