Matrix Operations

Adding and subtracting matrices is possible only when the two matrices have the same dimensions, i.e., they have the same number of rows and columns.

Below is an example of adding two matrices:

|A+B=\begin{pmatrix}
a & b\\
c & d
\end{pmatrix} +\begin{pmatrix}
e & f\\
g & h
\end{pmatrix}=\begin{pmatrix}
a+e & b+f\\
c+g & d+h
\end{pmatrix}=C|

When adding the matrices |A| and |B| , the result is the following:

|A+B=\begin{pmatrix}
6 & 5 & 4\\
4 & 3 & 5
\end{pmatrix}+\begin{pmatrix}
3 & 4 & 2\\
4 & 4 & 3
\end{pmatrix}=\begin{pmatrix}
6+3 & 5+4 & 4+2\\
4+4 & 3+4 & 5+3
\end{pmatrix}|

Thus, obtaining the new matrix |C|:

|\begin{pmatrix}
6 & 5 & 4\\
4 & 3 & 5
\end{pmatrix}+\begin{pmatrix}
3 & 4 & 2\\
4 & 4 & 3
\end{pmatrix}=\begin{pmatrix}
9 & 9 & 6\\
8 & 7 & 8
\end{pmatrix}=C|

Below is an example of subtracting two matrices:

|A-B=\begin{pmatrix}
a & b\\
c & d
\end{pmatrix} -\begin{pmatrix}
e & f\\
g & h
\end{pmatrix}=\begin{pmatrix}
a-e & b-f\\
c-g & d-h
\end{pmatrix}=C|

If matrix |B| is subtracted from matrix |A| in the example below:

|A-B=\begin{pmatrix}
3 & 4 & 4\\
5 & 4 & 6
\end{pmatrix}-\begin{pmatrix}
2 & 5 & 1\\
6 & 4 & 4
\end{pmatrix}=\begin{pmatrix}
3-2 & 4-5 & 4-1\\
5-6 & 4-4 & 6-4
\end{pmatrix}=C|

The new matrix |C| is obtained:

|A-B=\begin{pmatrix}
3 & 4 & 4\\
5 & 4 & 6
\end{pmatrix}-\begin{pmatrix}
2 & 5 & 1\\
6 & 4 & 4
\end{pmatrix}=\begin{pmatrix}
1 & -1 & 3\\
-1 & 0 & 2
\end{pmatrix}=C|

Here is an example of multiplying a matrix by a scalar:

|k\times\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}=\begin{pmatrix}
ka & kb\\
kc & kd
\end{pmatrix}|

|4\times\begin{pmatrix}
1 & 5 & 2\\
-1 & 7 & -3
\end{pmatrix}=\begin{pmatrix}
4 & 20 & 8\\
-4 & 28 & -12
\end{pmatrix}|

The product of matrix |A| and matrix |B| is possible if and only if the number of columns in the matrix |A| is equal to the number of rows in the matrix |B| .

Consider the multiplication of the following matrices:

|A_{m\times p}\times B_{p\times n}=C_{m\times n}|

The new matrix has the same number of rows as matrix |A| and the same number of columns as matrix |B|.

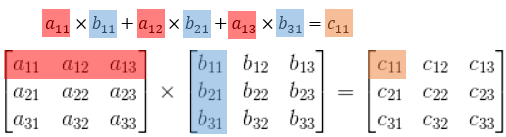
1. We multiply, in order, each element of a row in the first matrix |A| by each element of a column in the second matrix |B| and we continue to do this for all elements of the two matrices.

   |\small A \times B=\begin{pmatrix}
   {\color{Blue} 1} & {\color{Blue} 2}\\
   {\color{Red} 0} & {\color{Red} 4}\\
   3 & -1
   \end{pmatrix}\times\begin{pmatrix}
   {\color{Magenta} 2} & {\color{DarkGreen} 0}\\
   {\color{Magenta} 1} & {\color{DarkGreen} -3}
   \end{pmatrix}=\begin{pmatrix}
   {\color{Blue} 1}\times{\color{Magenta} 2}+{\color{Blue} 2}\times {\color{Magenta} 1} & {\color{Blue} 1}\times{\color{DarkGreen} 0}+{\color{Blue} 2}\times {\color{DarkGreen} -3}\\
   {\color{Red} 0}\times{\color{Magenta} 2}+{\color{Red} 4}\times {\color{Magenta} 1} & {\color{Red} 0}\times {\color{DarkGreen} 0}+{\color{Red} 4}\times {\color{DarkGreen} -3}\\
   3\times{\color{Magenta} 2}+-1\times {\color{Magenta} 1} & 3\times {\color{DarkGreen} 0}+-1\times {\color{DarkGreen} -3}
   \end{pmatrix}|

2. We add the products to obtain a new matrix.

   |\begin{pmatrix}
   {\color{Blue} 1}\times{\color{Magenta} 2}+{\color{Blue} 2}\times {\color{Magenta} 1} & {\color{Blue} 1}\times{\color{DarkGreen} 0}+{\color{Blue} 2}\times {\color{DarkGreen} -3}\\
   {\color{Red} 0}\times{\color{Magenta} 2}+{\color{Red} 4}\times {\color{Magenta} 1} & {\color{Red} 0}\times {\color{DarkGreen} 0}+{\color{Red} 4}\times {\color{DarkGreen} -3}\\
   3\times{\color{Magenta} 2}+-1\times {\color{Magenta} 1} & 3\times {\color{DarkGreen} 0}+-1\times {\color{DarkGreen} -3}
   \end{pmatrix}=\begin{pmatrix}
   4 & -6\\
   4 & -12\\
   5 & 3
   \end{pmatrix}|

Answer: The new matrix obtained is |C=\begin{pmatrix}
4 & -6\\
4 & -12\\
5 & 3
\end{pmatrix}|.

The multiplication of two matrices |A| and |B| is not commutative. Thus, |AB \neq BA| except in very special cases.