A matrix is an arrangement of m rows and n columns of numbers. In a matrix A with dimensions m × n:
- m represents the number of rows in the matrix;
- n represents the number of columns in the matrix;
- element amn corresponds to the element located at the intersection of the mth row and the nth column.
|A=\left(\begin{array}{ccccc}
a_{11} & a_{12} & a_{13} & \ldots & a_{1n}\\
a_{21} & a_{22} & a_{23} & \ldots & a_{2n}\\
a_{31} & a_{32} & a_{33} & \ldots & a_{3n}\\
\vdots & \vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & a_{m3} & \ldots & a_{mn}
\end{array}\right)|
A matrix is a structured rectangular table with data in rows and columns. Matrices are used, among other things, to express transformation rules when applying geometric transformations on a Cartesian plane.
Consider the following polygon ABCD:
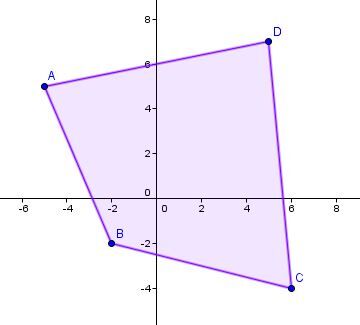
The coordinates of the polygon’s vertices can be presented separately using column matrices: |A=\begin{pmatrix}
-5\\
5
\end{pmatrix},
B=\begin{pmatrix}
-2\\
-2
\end{pmatrix},
C=\begin{pmatrix}
6\\
-4
\end{pmatrix}| and |D=\begin{pmatrix}
5\\
7
\end{pmatrix}| . It is also possible to write the vertices’ coordinates using row matrices: |A = \begin{pmatrix} -5 & 5 \end{pmatrix}, B= \begin{pmatrix} -2 & -2 \end{pmatrix}, C= \begin{pmatrix} 6 & -4 \end{pmatrix}| and |D=\begin{pmatrix} 5 & 7 \end{pmatrix}|,
or in a matrix written in two ways, as follows: |M=\begin{pmatrix}
-5 & -2 & 6 & 5\\
5 & -2 & -4 & 7
\end{pmatrix}| or |M=\begin{pmatrix} -5 & 5 \\ -2 & -2 \\ 6 & -4 \\ 5 & 7 \end{pmatrix}|
A matrix is generally designated by an uppercase letter (e.g., the matrix |A| ) and by each element that composes it with a lowercase letter.
The following matrix |A| is composed of 2 rows and 3 columns. This matrix has a dimension of |2 \times 3.|
|\begin{pmatrix}
2 & 5 & 4\\
-1 & 7 & -3
\end{pmatrix}|
It can be written as: |a_{23} = -3| and |a_{13} = 4|
Some matrices carry particular qualifiers when they present certain characteristics.
- Null matrix (or zero matrix): A null matrix is a matrix whose elements are only zero. It is written as |0_{m\times n}.|
|0_{2\times 3}=\begin{pmatrix}
0 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}|
- Row matrix: A row matrix is a matrix with a single row. The matrix is written as: |A_{1\times n}|.
|A_{1\times 3}=\begin{pmatrix}
2 & 3 & 0
\end{pmatrix}|
- Column matrix: A column matrix is a matrix with a single column. The matrix is written as: |A_{m\times 1}|.
|A_{3\times1}=\begin{pmatrix}
2\\
3\\
0
\end{pmatrix}|
- Square matrix: A square matrix is a matrix containing an equal number of columns and rows. The main diagonal of this matrix is made up of the elements: |a_{11}, a_{22}, ..., a_{nn}| .
|A_{4\times4}=\begin{pmatrix}
{\color{Green} 2} & 5 & 7 & -1\\
0 & {\color{Green} 3} & -4 & 5\\
1 & 3 & {\color{Green} 6} & 4\\
-2 & 0 & 4 & {\color{Green} 5}
\end{pmatrix}|
The main diagonal of the matrix is made up of the elements: |2, 3, 6, 5| .
- Diagonal matrix: A diagonal matrix is a square matrix where all the elements are zero except those located on the main diagonal. We denote the matrix as |A_{n\times n}|.
|A_{3\times3}=\begin{pmatrix}
3 & {\color{Red} 0} & {\color{Red} 0}\\
{\color{Red} 0} & -2 & {\color{Red} 0}\\
{\color{Red} 0} & {\color{Red} 0} & 4
\end{pmatrix}|
- Identity matrix: An identity matrix is a diagonal matrix where all the elements of the main diagonal are equal to 1. We denote the identity matrix as |I_{n\times n}|.
|I_{4\times4} = \begin{pmatrix}
{\color{Red} 1} & 0 & 0 & 0\\
0 & {\color{Red} 1} & 0 & 0\\
0 & 0 & {\color{Red} 1} & 0\\
0 & 0 & 0 & {\color{Red} 1}
\end{pmatrix}|
Note: In the identity matrix, elements that are not in the main diagonal cannot be different from 0.